2. 湖南省株洲市气象局, 株洲 412003;
3. 气象防灾减灾湖南省重点实验室, 长沙 410118;
4. 中国气象局地球系统数值预报中心, 北京 100081;
5. 灾害天气国家重点实验室, 北京 100081
2. Zhuzhou Meteorological Office of Hunan Province, Zhuzhou 412003;
3. Key Laboratory of Preventing and Reducing Meteorological Disaster of Hunan Province, Changsha 410118;
4. Center for Earth System Modeling and Prediction of CMA, Beijing 100081;
5. State Key Laboratory on Severe Weather, Beijing 100081
大气湍流是大气中重要的中小尺度过程,它影响着大气中的能量平衡和物质传输过程,使能量、动量、物质在不同尺度的运动之间转换,从而调整大气结构,使大气成分在一定的高度范围内均匀分布(Jaeger and Sprenger, 2007)。在大气边界层,湍流运动相当强,其对地面强迫的响应时间在1小时以内(刘辉志等, 2018)。对流层下部的湍流对地面附近动量和大气污染物的向上扩散有重要影响(Fritts et al, 2012),平流层顶的湍流对对流层和平流层之间的物质和能量交换有显著的影响(Dutta et al, 2009),自由大气中的湍流对航空的飞行安全会产生重要影响(Gerz et al, 2005)。因此,充分认识湍流的时空分布特征对于大气污染预报、天气预报和气候预测都相当重要。
考虑到大气热力结构、动力结构和湍流动能对湍流混合过程的共同影响(陈德辉等,1996),湍流运动具有相当强的间歇性和随机性,一般难以对湍流的性质进行准确、定量的描述,因此在数值模式中,常需要根据理论研究结果和观测资料对其效应进行参数化描述。湍流扩散系数是湍流参数化方案需要预报的关键物理量,但是其缺乏实时观测对模式结果来进行验证。湍流扩散系数可以由湍流耗散率进行诊断,因此本文首先利用高垂直分辨率探空资料对湍流动能耗散率进行了研究。湍流动能耗散率是描述湍流运动强度的一个重要物理量,它既可以影响对流层和平流层之间的质量、动量和能量以及化学物质的交换,也能影响各种波(重力波、行星波等)从热带对流层向高层大气的传播过程,进而影响低层与高层大气的耦合(Fritts et al, 1996)。因此,研究湍流动能耗散率的时空分布特征是十分迫切和必要的。
从高垂直分辨率探空资料获得湍流动能耗散率的信息,需要采用Thorpe分析法。Thorpe分析法最初由Thorpe (1977)提出,通过对实况海洋位势密度垂直廓线按照稳定层结条件进行垂直方向的重新排序,再将重排获得的稳定位势密度分布和实况位势密度分布比较,用位势密度所在位置的变化信息反演湍流翻转产生的位置和范围,这个方法被广泛应用于海洋湍流特征的分析。Clayson and Kantha(2008)提出将其用来估计自由大气中的湍流参数,把过去几十年一直用于海洋稳定层结的方法创新性地应用于具有稳定层结特点的自由大气中,利用大气中的保守量位温按照稳定层结要求的分布调整,产生的位置翻转(翻转指对原始位温与按照稳定层结分布要求重新排列产生的位温位置的差异)反演大气的湍流特征。在利用Thorpe分析法研究和分析大气湍流耗散率方面,国外已经进行了不少研究工作。Wilson et al(2010;2011)对Thorpe分析法进行了进一步改进,考虑了仪器噪音的影响,使对湍流识别的准确率得到提高。Wilson et al(2013)又考虑了湿度对Brunt-Väisälä频率的影响,把Thrope方法的研究范围从晴空扩展到有云大气,至此Thorpe分析法估算大气湍流特征的方法趋向成熟。近年,Zhang et al(2019a;2019b)采用美国的7个中纬度站点的2012年1月至2016年12月的高分辨率探空数据,验证了Thorpe分析在大气湍流统计研究中的可信度。2019年还通过对美国高分辨率探空仪数据集进行Thorpe分析,研究了湍流的纬度依赖和地形相关性;同年Ko et al(2019)基于美国的高垂直分辨率探空数据(2012年9月至2016年8月),在68个业务运行台站用Thorpe分析法分析了美国区域自由大气中的Thorpe尺度和涡流耗散率,这是少数几个在比较广的时空范围内,利用高分辨率探空观测资料研究湍流参数分布特征的工作。在国内的研究中,Liu et al(2014)利用Thorpe分析法,基于南海考察船上观测到的热带海洋对流层上部的无线电探测资料,研究了这个考察站对流层上层湍流参数的日变化,及其与中尺度对流系统日变化的密切关系,之后又分别采用Thorpe分析法和利用气球垂直上升速度的扰动计算湍流参数的方法,计算南海同样这个考察站对流层和低平流层的湍流动能耗散率和湍流扩散系数,并比较分析了两种方法的优劣。近期,Lv et al(2021)使用中国120个站点的高垂直分辨率探空仪数据(2011年1月至2018年12月),计算了自由大气中大气湍流的Thorpe尺度和湍流动能耗散率,弥补了我国此前没有在较广的时空范围内研究湍流参数分布的不足,但是他们的研究没有分析不同下垫面上湍流参数分布的差异;同时,他们的研究结果虽然考虑了Wilson et al(2010)建议的仪器噪音的消除,但是没有详细分析中国的仪器噪音对结果的影响,因此本论文将对这个影响进行讨论。
Wilson et al(2010)最早发现在利用秒级探空资料研究湍流时,仪器噪音的影响会对分析结果产生比较大的影响。仪器噪声会产生虚假的位置翻转和虚假的湍流识别。若将虚假湍流层计入真实的湍流层中,会导致对湍流发生频率的严重高估,从而导致对大气湍流参数和湍流能量的高估,湍流的时空不均匀性会导致扩散系数估计值偏差超过几个数量级。这些虚假翻转很难与湍流产生的真实翻转区分开来,因此对观测资料进行去除仪器噪音过程非常重要(Thorpe,1977;Galbraith and Kelley, 1996;Ferron et al,1998;Gargett and Garner, 2008)。Wilson et al(2010)基于统计方法提出了去除仪器噪声影响的方法,首先推导了可探测的湍流层大小的阈值与整体趋势噪声比的函数关系,提出了只有反演的垂直尺度超过相同大小正态分布的噪声样本的范围(最大和最小值之差)的规定百分位数,才能将其识别为真实的翻转。本文将把这一方法应用到中国的高垂直分辨率秒级探空资料,研究在利用Thorpe分析法对中国区域的湍流耗散率进行分析时仪器噪音对分析结果的影响。
已有很多研究证明空气的流动情况受下垫面的影响很大:刘明星等(2008)利用相同探测设备、相同试验方法在戈壁、草原、郊区和城郊等不同下垫面开展的多次重复湍流观测试验资料, 采用相同的湍流数据采集和处理方法, 研究了不同下垫面温度和湿度湍流谱特征,发现高粗糙度下垫面的高频段谱曲线高于平坦地形, 说明高粗糙度地区的局地湍流耗散较强,戈壁下垫面的低频段湿度谱数值明显高于其他地区;洪雯和王毅勇(2010)总结了水平非均匀下垫面的大气边界层研究,指出干旱区的绿洲具有明显的“冷湿岛效应”,并可形成边缘逆湿和区域环流,而植被和水域的分布则显著改变了大气边界层结构。同时还阐述了复杂地形下垫面对局地风场和小尺度环流产生的影响、城市热岛效应的产生及特点和城市中绿地和水体的微气候效应;龚玺等(2018)利用国家气候中心2009—2011年在内蒙古锡林浩特市、河北黄骅市、江西湖口县和星子县开展的100 m铁塔大气湍流观测试验数据,分析不同下垫面、不同稳定度条件下地面到100 m的风切变指数变化情况, 发现下垫面与风切变指数变化有密切联系。但是之前的研究没有详细分析不同下垫面情况下的湍流参数分布特征。我国的下垫面种类相当丰富,根据国家地球系统科学数据中心的数据,我国的下垫面类型多达24种。空气流动受下垫面影响的方式主要有两种:一是动力作用,如地形起伏、植被或者建筑物等改变地面粗糙度可增加动力湍流;二是下垫面的热力作用,因地形起伏或水陆分布,使得下垫面受热和散热不均匀,从而引起温度场和风场的变化,进而影响湍流的产生,因此下垫面对于湍流的强弱以及频率都会有较强的影响作用。在研究下垫面与湍流分布特征的关系方面,潘乃先等(1993)利用三分量风速仪采集风的资料,研究了不同下垫面近地层上的湍流度统计特征,结果表明中性大气条件下湍流度的统计平均值与地表起伏状况存在紧密的关系, 并表现出一定的规律性;涂钢等(2009)分析了2003—2005年半干旱区退化草地和农田下垫面近地层湍流通量日、季、年的变化特征, 探讨了不同年份的气候背景和下垫面土地覆被对地气交换过程的影响,得出了结论:半干旱区退化草地和农田近地层湍流通量具有明显的日变化、季变化周期,地气间通量交换年际间的差异主要受当年的气候背景影响, 同时还受到降水、下垫面覆被的影响;王少影等(2010)利用“绿洲系统能量与水分循环过程观测试验”2005年绿洲、戈壁点的观测资料, 分析与讨论了温度、水汽的归一化标准差随稳定度变化的通量方差关系; 张璐等(2021)通过改变鲍恩比的敏感性试验研究不同大气初始状况下,湿润和干旱下垫面湍流特征及其对深对流触发过程的影响,结果表明:干旱下垫面的混合层干而暖,厚度较大,湿润下垫面相反,边界层内的深对流首先在干旱下垫面发生;张蕴帅等(2021)对比分析了黄河源区两种不同下垫面上(鄂陵湖和湖边草地)对流边界层(CBL)中精细的湍流结构特征,发现两个不同下垫面上模拟结果对模式分辨率的敏感性不同,也模拟出了各种尺度的波对湍流通量的累积贡献。但是这些研究中有的只局限于局部地区和近地层的高度,没有对东亚整个区域以及自由大气高度范围进行研究;有的虽然考虑了一定的范围,但并没有分析湍流动能耗散率的分布情况。
因此,本文利用2011年1月1日至2018年12月31日我国的高垂直分辨率探空资料,分析在中国区域的仪器噪音对Thorpe分析法估算湍流动能耗散率的影响;同时研究东亚不同下垫面特征条件下,湍流动能耗散率的变化特征。
1 资料和方法 1.1 高垂直分辨率探空数据本文用于估算湍流动能耗散率的数据来自国家气象信息中心提供的中国无线电探空观测网的高垂直分辨率的探测数据(Guo et al,2014;2016)。如图 1所示,自2011年至今已有120个无线电探空站升级为L波段探空。郝民等(2014)使用2011年6—7月的L波段探空资料进行分析,结果发现秒级探空资料在850 hPa、500 hPa等层次上高度分析比传统探空分析更接近NCEP分析,显示出对分析场的改进效果,同时风场在200 hPa以上的高层分析中改进显著,表现出高分辨率资料使用在高层分析中对系统模拟更加准确的特征。L波段探空仪主要由GFE(L)型高空气象探测雷达和GTS1型数字探空仪组成,气压、温度、风速等气象要素的数据采集由GTS1型数字探空仪完成。GTS1型探空仪的测量周期为1.2±0.1 s,每分钟采集50次,气球以400 m·min-1的速度上升,因此探测资料的垂直分辨率达到4 m,具有很高的垂直分辨率和实时采集能力(杨湘婧等,2011;Guo et al, 2019),其测量的温度、气压、位势高度一致性较好,风向风速与GPS导航卫星定位测风的结果比较接近(李伟等,2011)。每天分别在08时和20时(北京时,下同)两次提供温度、相对湿度、压力和风速的垂直廓线。本文使用的高垂直分辨率探测数据的时间段为2011年1月1日至2018年12月31日,绝大多数台站都有比较多的观测样本。在本研究中,为了保证足够长的垂直范围,高度范围小于12 km的探空数据将被舍弃。大多数探空观测的最大高度高于25 km,这表明在分析范围内有足够多的观测样本。由于气球的垂直上升速度是变化的,观测的间距是非等距的,为了便于分析研究,本文首先使用三次样条插值把原始数据插值到10 m等距的垂直格点上。
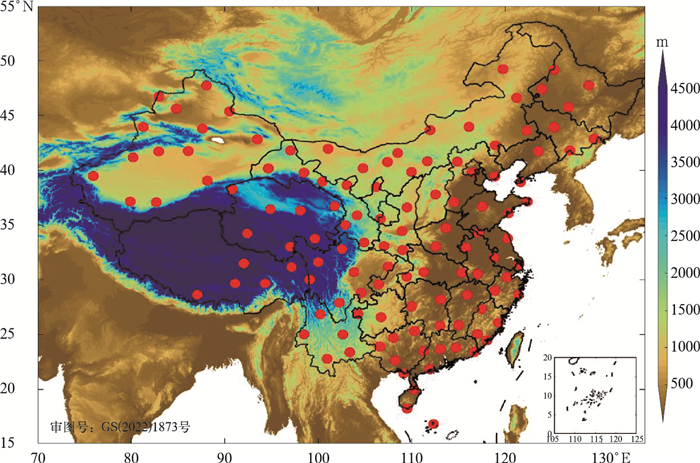
|
图 1 我国120个探空站点的分布 注:红色点为站点,底图为对应的地形高度。 Fig. 1 Distribution of 120 sounding stations (red point) in China |
空气一般有三种状态,干空气、未饱和和饱和状态。由于水汽对未饱和空气的影响比较小,因此只需要考虑干空气和饱和空气两种情况(Wilson et al, 2014)。本文基于Zhang et al(2010)的研究,用探空仪测量的相对湿度(RH)是否满足两个随高度变化的阈值条件RHmax和RHmin(表 1), 从而确定大气是否饱和(即是否存在云)。
|
|
表 1 判别云层存在的相对湿度阈值随高度的变化(Zhang et al, 2010) Table 1 Variation of relative humidity threshold for judging the existence of clouds with height (Zhang et al, 2010) |
判断条件为,如果某一高度范围内的所有层的RH≥RHmin(随高度变化),并且此范围内同时存在某一个高度的RH≥RHmax(随高度变化),则这一高度范围被确定为有云层。
参照Wilson et al(2013)、Luce et al(2014)的研究方法,针对晴空和有云层分别使用以下公式计算位温:
| $ \theta(i)=\theta(i-1)\left[1+N_{\mathrm{d}}^2(i-1) \frac{\Delta z}{g}\right] $ | (1) |
| $ \theta(i)=\theta(i-1)\left[1+N_{\mathrm{m}}^2(i-1) \frac{\Delta z}{g}\right] $ | (2) |
式(1)用于干空气层,式(2)用于有云大气层。式中: g是重力加速度,Δz为高度差,Nd2是干的Brunt-Väisälä频率的平方,可表示为:
| $ N_{\mathrm{d}}^2(i-1)=\frac{g}{\theta(i-1)}\left(\frac{\mathrm{d} \theta}{\mathrm{d} z}\right)_{i-1} $ | (3) |
而Nm2是湿的Brunt-Väisälä频率的平方,可以表示为(Durran and Klemp, 1982):
| $ \begin{gathered} N_{\mathrm{m}}^2(i-1)=\frac{g}{T(i-1)}\left[\left(\frac{\partial T}{\partial z}\right)_{i-1}+{\mathit{\Gamma}}_{\mathrm{m}}(i-1)\right] \times \\ {\left[1+\frac{L_{\mathrm{v}} q_{\mathrm{s}}(i-1)}{R T(i-1)}\right]-\frac{g}{1+q_{\mathrm{w}}(i-1)}\left(\frac{\mathrm{d} q_{\mathrm{w}}}{\mathrm{d} z}\right)_{i-1}} \end{gathered} $ | (4) |
式中: Lv是凝结潜热,总混合比qw=ql+qs,ql是云水/冰混合比,qs是水汽饱和混合比。由于无法得到云水/冰混合比的信息,且其值相对水汽饱和混合比比较小,因此忽略,近似qw=qs。Γm是湿绝热递减率(Durran and Klemp, 1982):
| $ \begin{aligned} & {\mathit{\Gamma}}_{\mathrm{m}}(i-1)=\frac{g}{c_{\mathrm{pd}}}\left[1+q_{\mathrm{w}}(i-1)\right] \times \\ & {\left[1+\frac{c_{\mathrm{pv}} q_{\mathrm{s}}(i-1)+c_{\mathrm{w}} q_1(i-1)}{c_{\mathrm{pd}}}+\right.} \\ & \left.\frac{\gamma L_{\mathrm{v}}^2 q_{\mathrm{s}}(i-1)}{c_{\mathrm{pd}} R T^2(i-1)}\left(1+\frac{q_{\mathrm{s}}(i-1)}{\gamma}\right)\right]^{-1} \end{aligned} $ | (5) |
式中: cpd为干空气的比热容,cw为水/冰的比热容,cpv为水汽的比热容,γ≈0.622,ql项同样被忽略。
由式(1)、式(2)计算得出位温θ后,将其按从小到大的顺序进行重排,得到的重排的位温被称为θ*。如果原θ廓线上位于高度z处的值,在θ*廓线中位于高度zs处,则其Thorpe位移可以定义为:LD(z)=z-zs(即调整之前的高度减调整之后的高度)。如果在任意高度上发生了位移,则意味着相反方向的位移必然发生在其他某个点。因此,当从大气低层向上积分到累积的Thorpe位移满足以下公式时,可确定为湍流层(Wilson et al,2010):
| $ \sum\limits_{i=1}^n L_{\mathrm{D}}(i)=0 $ | (6) |
| $ \sum\limits_{i=1}^k L_{\mathrm{D}}(i)<0 $ | (7) |
式中:k < n(Wilson et al,2010)。利用式(6)和式(7)确定湍流层后,计算每个湍流层中Thorpe位移的均方根即为Thorpe尺度。如Dillon(1982)所述,Thorpe方法的基本假设在于Thorpe尺度(LT)与Ozmidov尺度(LO)成线性比例,表示为:
| $ L_{\mathrm{O}}=c L_{\mathrm{T}} $ | (8) |
式中:c是一个常数,且在以前的研究中已被广泛讨论(Dillon,1982;Sunilkumar et al,2015; Zhang et al,2019)。Ozmidov尺度同时也可以表示为:
| $ L_{\mathrm{O}}=\left(\frac{\varepsilon}{N^3}\right)^{\frac{1}{2}} $ | (9) |
式中: ε表示湍流耗散率,N表示Brunt-Väisälä频率。结合式(8)和式(9),可以得出ε为:
| $ \varepsilon=C_{\mathrm{K}} L_{\mathrm{T}}^2 N^3 $ | (10) |
式中CK=c2,最近的数值试验表明,CK随湍流的时间演变而变化,并随着时间的推移而增加(Fritts et al, 2016)。然而,Sunilkumar et al(2015)的研究又发现CK呈明显的对数正态分布。因此,CK的平均值通常被视为一个接近常数的值,这使得Thorpe分析成为可能,从而从统计角度估计湍流。最近一项基于蒙特卡罗模拟的研究(Zhang et al,2019b)进一步证实了这一点,该研究表明CK保持接近常数,其最佳预测值为0.54,因此接下来的分析中都取CK=0.54。
为了更好地描述垂直分布的特征,将其分成四个高度间隔进行研究:对流层下部(LT)、对流层上部(UT)、平流层下部(LS)和平流层上部(US),它们的范围分别为2~7、7~12、12~20和20~25 km。
1.3 仪器噪音利用探空观测资料估算湍流时,仪器噪声的影响是一个不可忽视的问题。仪器噪声会产生虚假湍流层,很难将其与真实湍流层区分开来(Thorpe,1977;Galbraith and Kelley, 1996;Ferron et al,1998;Gargett and Garner, 2008),然而在很多早期估算大气湍流的研究中,噪声问题都被忽略了。若将虚假湍流层计入真实的湍流层中,会导致对其发生频率的严重高估,从而导致对大气湍流参数和湍流能量的高估。
Wilson et al(2010;2011)提出了一种基于统计识别仪器噪声的方法,即使用趋势噪声比(trend-to-noise ratio, TNR)来评估测量的噪声水平。TNR可分为两类:一类是局部的趋势噪声比(以下称为局部TNR),用于评估各高度处的噪声水平;另一类是用于确定θ总体质量的整体趋势噪声比(以下称为整体TNR)。这里简要介绍去噪声的过程:(1)首先将每一个温度的观测廓线均分成长度为200 m长的区间,由于数据的分辨率为10 m,因此每20个点为一组;(2)再将每一个区间分别进行线性拟合,然后从每一段中剔除线性拟合的结果;(3)计算剔除拟合结果的温度廓线的一阶差分的方差,该值的一半即是观测温度噪声的方差;(4)最后将温度的噪声标准差进行光滑处理。
得到仪器的温度噪声标准偏差σT后,由
| $ \sigma_\theta=\theta \sqrt{\frac{\sigma_{\mathrm{T}}^2}{T}+\frac{2}{7} \frac{\sigma_{\mathrm{P}}^2}{p}} \approx \theta \frac{\sigma_{\mathrm{T}}}{T}=\left(\frac{1000}{p}\right)^{2 / 7} \sigma_{\mathrm{T}} $ | (11) |
式中:θ用重排后的位温,σθ是位温的噪声, p, T分别为原始的气压和温度, 整体TNR计算如下:
| $ \bar{\zeta}=\frac{\theta(n)-\theta(1)}{(n-1) \sigma_\theta} $ | (12) |
式中n是研究范围内所有样本的总数,整体TNR是相对于仪器噪声的湍流信号强度的指标。一般来说,整体TNR越低,说明信号的强度越弱,出现虚假湍流层的概率越高。因此,如果整体TNR太小(在对流层一般小于0.80),则需要进行去噪音处理。最后,在一个湍流层范围内θ*的变化应超过该厚度内同样样本大小的噪声样本范围的99%。可以识别的湍流层厚度的大小与阈值TNR之间的统计相关性如Wilson et al(2010)研究的图 5所示。低于标准的湍流层被标记为假,需要被剔除。关于仪器噪音对湍流耗散率的影响将在2.1节中进行介绍。
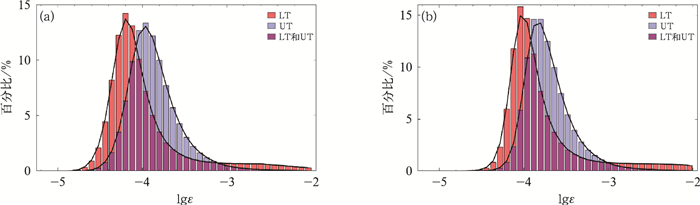
|
图 2 2011—2018年考虑仪器噪音(a)前, (b)后的对流层下层(LT:2~7 km)、对流层上层(UT: 7~12 km)的lgε的百分比分布 注:黑线显示了对数正态分布。 Fig. 2 The lgε percentage distribution of the lower troposphere (LT: 2-7 km) and the upper troposphere (UT: 7-12 km) (a) before and (b) after the instrument noise considered during 2011-2018 |
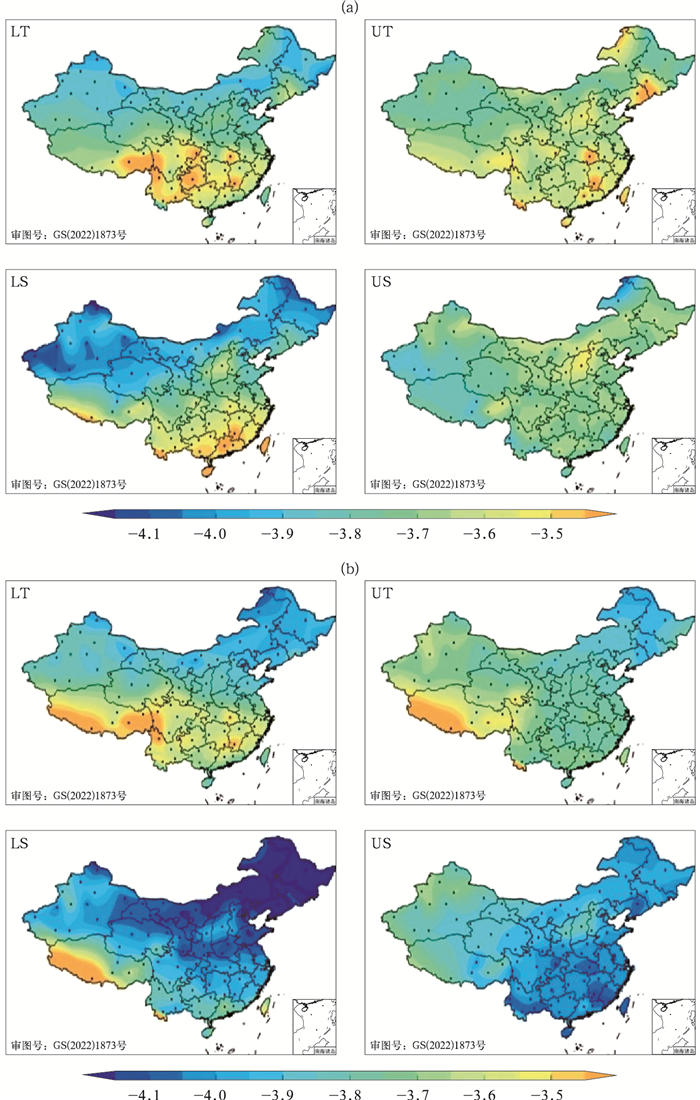
|
图 3 2011—2018年(a)08时,(b)20时4个高度层平均的大气湍流耗散率lgε的水平分布 注:LT、UT、LS、US的垂直范围分别为2~7、7~12、12~20和20~25 km。 Fig. 3 The horizontal distribution of average atmospheric turbulence dissipation rate lgε at four altitudes at (a) 08:00 BT, (b) 20:00 BT from 2011 to 2018 |
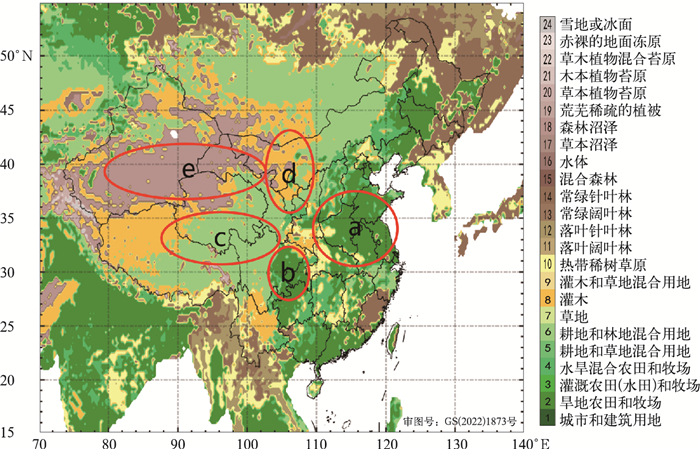
|
图 4 我国24种下垫面类型分布 注:红圈标出研究选择的下垫面区域,a为水田作物下垫面, b为旱地作物下垫面, c为草地下垫面, d为灌木下垫面, e为荒地下垫面。 Fig. 4 Distribution of 24 types of underlying surfaces in China |
|
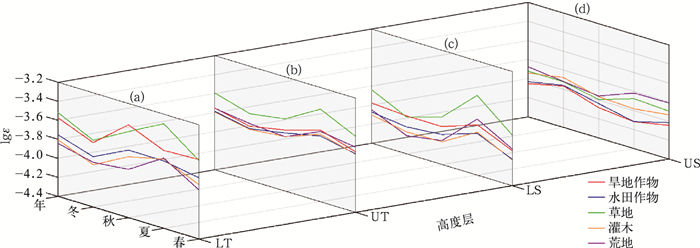
图 5 2011—2018年年平均和季节平均的旱地作物(红色)、水田作物(蓝色)、草地(绿色)、灌木(黄色)和荒地(紫色)在4个高度层平均的lgε分布(a)对流层下层, (b)对流层上层, (c)平流层下层, (d)平流层上层 Fig. 5 The annually averaged and seasonally averaged lgε distributions of dry land crops (red), paddy crops (blue), grassland (green), shrubs (yellow) and wasteland (purple) at four height levels from 2011 to 2018 (a) lower troposhere, (b) upper troposphere, (c) lower stratosphere, (d) upper stratosphere |
由于仪器噪音会使得探测时产生虚假的湍流层,从而使后期计算的湍流耗散率产生偏差。而在使用式(11)和式(12)进行了整体TNR的计算后,发现未考虑仪器噪音时,对流层的整体TNR难以达到规定的0.8(一般为0.7),而平流层则可以达到1以上。因此在本节中,我们将主要分析在对流层中中国的探空仪器噪音对于ε估算的影响。图 2显示了降噪前后的2011—2018年对流层(LT和UT)的湍流动能耗散率ε值的分布情况。需要注意的是,因为值比较小,ε用对数标度表示,其值是根据式(10)计算得出的。
由图 2可知,lgε的范围为-5~-2。从整体分布看,无论是在对流层低层还是上层,ε的分布近似对数正态分布,呈正偏斜。在考虑噪声前,lgε在低层和上层的平均值分别是-3.9444(ε=1.137×104 m2·s-3)和-3.8594(ε=1.382×104 m2·s-3),上层的均值要稍大于低层,这表明上层中的湍流层要强于低层;而在考虑噪声后,lgε在低层和上层的平均值分别变为了-3.7228(ε=1.893×104 m2·s-3)和-3.6991(ε=1.999×104 m2·s-3),这意味着噪音产生了一些小尺度的虚假湍流层,使对流层平均的湍流耗散率偏小,证明了去除噪音的必要性。
2.2 不同下垫面上的湍流动能耗散率水平分布特征图 3显示了2011—2018年08时和20时4个高度层的大气湍流耗散率的水平分布。总体而言,对流层上层的湍流最强,对流层下层与平流层下层次之,平流层上层最弱。值得注意的是,以复杂地形为特征的青藏高原在所有高度层都出现了强的峰值,这和在落基山脉地区湍流比较强的结论是一致的(Ko et al,2019), 这是由于大地形有比较大的粗糙度,对形成湍流的动力作用有较大影响,同时研究表明这个地区的感热通量也比较大,热力作用也对湍流的产生起了很大作用。平流层在这个区域湍流比较强,与青藏高原产生的地形重力波的上传和破碎有关(Liu et al, 2009)。相反,东北地区在各个高度层都表现出低值,在平流层下层尤为显著,说明该地区的湍流较弱,与这个地区温度偏低,大气常处于稳定状态有关。除平流层上层以外,湍流动能耗散率的年平均值呈现“南高北低”的型式,即在中国南方地区的湍流动能耗散率普遍比北方强,这可能是由于对流云经常占主导地位,频繁的对流作用对湍流有促进作用,尤其是在夏季(Li Z Q et al, 2016; Guo et al,2018),同时由于低纬地区下垫面温度比较高,热力作用比较大。此外,也可以发现除了主要的“南高北低”型式,对流层和平流层下层有比较明显的经向差异,尤其是对流层下层,这与低层大气受下垫面的影响比较大,随高度增加下垫面的影响逐渐减少有关。在平流层上层湍流动能耗散率的分布比较均匀,下垫面的影响几乎看不见,青藏高原的高值区也消失了,说明青藏高原对湍流的影响要低于20 km。综合而言,对流层(LT和UT)大气湍流的强度比平流层(LS和US)强得多。湍流动能耗散率水平分布的南高北低,垂直分布在对流层上层最强,大地形(例如落基山脉)上空为高值区的结论,与在美国和挪威使用相同Thorpe分析法基于美国和挪威的高垂直分辨率探空资料的研究结果非常相似(Li Q et al,2016;Ko et al,2019;Zhang et al,2019b)。
结合08时和20时不同高度层平均的水平分布可看出,在青藏高原的东西部各存在两个湍流高值区,这与青藏高原西部和东部的主要下垫面类型不同有关,西部主要是灌木,东部主要是草地。位于青藏高原西部的湍流区在08时较弱,在20时则较强,这表明该地区的湍流有较强的日变化;但是这个区域除了在平流层高层以外,各高度层平均强度垂直变化不大,这可能与灌木的影响高度比较高,以及这个区域日出时间较晚有关。而位于青藏高原东部的湍流区08时和20时变化不明显,日变化较弱,但垂直变化较明显,湍流强度在对流层低层最大,对流层高层和平流层下层逐渐减小,在平流层上层基本消失。这表明随着高度的增加,影响其强度的主导因素逐渐减弱,由此推测该地区产生强湍流的主导因素是下垫面。该湍流区及其附近地区下垫面类型均为草地下垫面,但湍流区范围并未与下垫面范围完全一致,可能是因为该地区位于横断山脉地区,随纬度变化高度落差较大,也造成了湍流的差异。而分布在长江中下游地区和华南地区的站点主要为水田和牧场下垫面类型(以下简称水田作物下垫面),该类型下垫面的作物类型多为水生作物,土地含水量大,且该类型站点数量最多,数据具有更高的可信度,虽然个别站点出现了极值,但整体分布情况较为均衡,较北方地区而言稍大。西南地区东部的主要下垫面类型为旱地农田和牧场(以下简称旱地作物下垫面),由于旱地农田无灌溉设施,主要靠天然降水种植旱生农作物,因此该下垫面类型的含水量与降水密切相关,中国农田变化对气候影响具有冬季弱、夏季强的季节性变化(曹富强等,2015),推测旱地下垫面的湍流强度和频率受季节变化影响较大。在内蒙古西部的下垫面类型为灌木下垫面,该区域在各高度层中湍流强度均较均匀,与下垫面条件比较均匀有一定关系。在新疆地区的下垫面类型为荒芜稀疏的植被下垫面(以下简称荒地下垫面),其湍流强度与灌木下垫面类型的站点数据较为接近。湍流的垂直分布与下垫面的关系将在下面的2.3节中做进一步深入研究。
2.3 不同下垫面上湍流动能耗散率的垂直分布特征为详细分析下垫面对湍流作用的影响,考虑到中国区域主要的下垫面类型,并根据2.2节分析的我国湍流水平分布特点,重点选择了5个不同类型的下垫面区域:旱地作物、水田作物、草地、灌木、荒地(图 4),将其中站点的数据样本进行平均来研究讨论。这些区域的选择既保证了下垫面的代表性,又保证了足够的样本数量,并且5个区域的纬度差异较小,在一定程度上排除了太阳高度角的季节变化对湍流强度的影响。
表 2给出了选取的5种类型下垫面区域的平均海拔、主要植被类型、干湿分区和主要气候类型。可以看出,选择的5种下垫面类型中的草地和荒地由于位于我国西部高原地区,平均海拔较其他类型明显更高。5种下垫面类型在干湿分区上也有较明显的差异,表明其对应的降水量和土壤含水量也有差别;这也导致了不同类型下垫面主要植被类型的差异。例如草原地区的植物大多是适应半干旱气候条件的草本植物;而荒漠的生态条件极为严酷,夏季炎热干燥,土壤贫瘠,因此植被稀疏,植物种类也很贫乏。本文选取的5种下垫面类型对应的气候类型也很多样,几乎涵盖了我国所有的主要气候类型,具有较好的代表性。
|
|
表 2 5种下垫面类型区域的基本特征 Table 2 Basic characteristics of five underlying surface types |
图 5给出在5个选择的不同下垫面区域,4个垂直分层平均的湍流动能耗散率的季节平均和年平均。结合图 5与表 2来看,在几乎全部下垫面的所有垂直分层,湍流均表现出了较强的季节性分布,即夏季最强,春秋季次之,冬季最弱。在下垫面影响最大的对流层(LT和UT),全年平均草地下垫面的湍流最强,水田作物下垫面、灌木下垫面、荒地下垫面的强度较为接近。旱地作物下垫面的湍流在对流层低层和对流层上层的差异很大,其在对流层低层很强,与草地相当接近,而在对流层高层则比较弱,与水田作物下垫面、灌木下垫面和荒地下垫面比较一致。旱地作物下垫面在对流层下层湍流较强的原因,可能是所选择的区域为南方的旱地,虽然其干湿分区上位于湿润地区,但其主要位于一些山地、丘陵地区,这些地区没有水源保证,且多为坡地,下垫面相对比较干燥,感热通量比较大,而土壤热通量在下垫面能量平衡研究中极为重要,是影响其湍流强度的重要因素(岳平等,2012)。草地下垫面的湍流最强,原因除了其主要植被类型为草原,能产生较大粗糙度以外,同时该区域的气候类型为高山高原气候,海拔较高,太阳辐射强、地气温差大,是强大的地面感热输送源,更容易产生湍流。除此之外,强湍流也和这个区域同时存在较为复杂的地形有关。从季节平均来看,荒地下垫面在各个季节均表现为最低,与之相反,草地下垫面在除秋季以外的各个季节均为最高。灌木与荒地下垫面除在对流层下层的秋季表现出一定差异以外,分布情况较为重合,这可能是由于两种下垫面在气候环境与地理位置上较为接近,都为温带大陆性气候,灌木虽然较荒地而言降水量更大,但两者的植被类型都为耐旱的低矮植物,对湍流的影响有限。水田作物下垫面稍强,但随四季的分布曲线最为平稳,季节性变化最弱,可能由于水田类型的下垫面降水量大,导致土壤含水量大,热容量大,因此季节变化比较小。
在平流层下层,从全年平均来看,草地下垫面的湍流依旧最强,旱地作物下垫面次之,水田作物下垫面稍弱于荒地,其下则是灌木。与对流层一样,灌木和荒地下垫面的湍流分布情况较为重合,但在春夏季出现了一定差异。在平流层上层各类型下垫面的差异较小,也就是说下垫面对湍流的影响只能到平流层下层的高度。草地在平流层上层以下各高度最强可能也与这个区域海拔比较高,地形的影响比较大有关。值得注意的是,灌木下垫面的湍流强度相较对流层,降低幅度很大。从季节平均来看,秋冬季各下垫面类型的强弱对比与年均基本一致,而春夏季不同,荒地明显增加,强于除草地之外的下垫面类型。在对流层湍流强度最强的草地下垫面在平流层下层各个季节依然很强,其随季节的变化也更加明显。在平流层上层,由于该层发生的湍流频率和强度都较弱,与下垫面的联系也最弱,因此5种下垫面的曲线相较其他高度层较为重合,且季节变化性也最弱,这也是合理的。
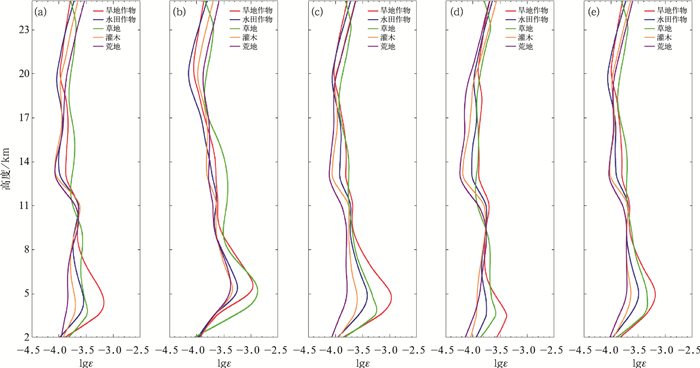
图 6给出了在垂直方向上,在不同下垫面的湍流动能耗散率的季节平均和全年平均的垂直廓线。从图上可以看出,5种下垫面在12 km附近出现了较大程度的重合,该高度正好位于对流层顶附近,这说明下垫面对于湍流的影响主要作用范围在对流层,在其之上的高度,下垫面的影响将会在一定程度上减弱。从季节平均来看,各下垫面类型4个季节均在2~6 km范围内均出现最大值,尤其是旱地作物。除夏季以外,旱地作物的极大值均大于其他下垫面的最大值。因为旱地在四季含水量都比较小,感热通量比较大,且其气候类型为亚热带季风气候,冬季温度相对较高,从而使得其在四季均有湍流高值,而在降水最强的夏季,各下垫面的含水量均会上升,潜热通量变大,湍流加强,因此草地下垫面的湍流在此时强于旱地作物下垫面,夏季还会产生频繁的对流云,而对流云也是湍流的主要来源(Storer et al,2019)。水田作物在各个季节的湍流强度均弱于旱地作物和草地,但是其季节性变化最小,因为水田靠人工灌溉,各个季节土壤含水量变化相对较小。灌木和荒地由于其植被类型和气候类型的相似性,湍流强度在各个季节都较为接近,但年平均灌木稍强,这可能与灌木区域的植被覆盖率更大有关。在12~20 km范围内,由于下垫面随高度增加产生的影响减弱,各下垫面的湍流均变化缓慢,草地下垫面开始明显强于旱地作物下垫面,其他3种下垫面的强度排名则与对流层一致,即水田强于灌木,灌木强于荒地。在20 km以上,各下垫面的湍流强度均有所上升,但分布线更为重合,说明下垫面的作用难以影响至该高度层,这与图 5得出的结论一致。
|
图 6 旱地作物(红色)、水田作物(蓝色)、草地(绿色)、灌木(黄色)和荒地(紫色)平均湍流的lgε分布(a)春季, (b)夏季, (c)秋季, (d)冬季, (e)年平均 Fig. 6 The lgε distributions of average turbulence of dry land crops (red), paddy field crops (blue), grassland (green), shrub (yellow) and wasteland (purple) (a) spring, (b) summer, (c) autumn, (d) winter, (e) annual average |
本文利用Thorpe分析法,基于秒级探空资料,研究了2011—2018年期间中国全天空(包括晴天和有云)条件下湍流耗散率的时空分布与下垫面的关系。同时讨论了中国的探空仪器噪音对用Thorpe分析法分析湍流的影响。得到以下主要结论:
(1) 仪器噪音会使得探测时产生虚假的湍流层,从而使后期计算的湍流耗散率产生偏差。从整体分布看,无论是在对流层低层还是上层,ε的分布近似对数正态分布,呈正偏斜。
在考虑噪声前,上层中的湍流层要强于低层;而在考虑噪声后,lgε在低层和上层的平均值均变大,这意味着噪音产生了一些小尺度的虚假湍流层,使对流层平均的湍流耗散率偏小,证明了去除噪音的必要性。
(2) 在考虑湿饱和效应的情况下,即在全天空条件下,自由大气的湍流耗散率的年平均分布在空间上表现出明显的“南高北低”和“西高东低”的型式。在中国南方地区的湍流动能耗散率普遍比北方强,这是由于对流云经常占主导地位,尤其是在夏季,频繁的对流作用对湍流有促进作用。而青藏高原上的强湍流可能是由于复杂的下垫面和地形的影响。从垂直分布来看,对流层上层的湍流比其他层次要强,和下垫面的动力和热力作用还可以影响到这一层,以及地形产生的重力波的破碎有关系。
(3) 湍流在不同下垫面均表现出明显的季节性,且夏季对流层上层的强度和频率最高。旱地作物特有的耐旱和蓄水性会使得下垫面的含水量在四季保持稳定,从而使得其在四季均有最大值,而在降水最强的夏季,各下垫面的含水量均会上升,潜热通量变大,湍流加强,因此草地下垫面的湍流在此时强于旱地作物下垫面。夏季还会产生频繁的对流云,而对流云也是湍流的主要来源。由于中国地处东亚季风区,对流具有明显的季节循环,和季风盛行和西太平洋副热带高压的季节性活动有密切关系。对流对湍流的影响还需要更深入的研究。
(4) 通过选定5个类型的下垫面具体分析表明,湍流的强度与对应下垫面类型有很大的联系,在受下垫面影响最大的对流层(LT和UT),全年平均分布上草地与旱地作物下垫面的湍流都较强,然后依次是水田作物下垫面、灌木下垫面、荒地下垫面。而在平流层下层(LS),旱地下垫面的湍流强度相较对流层,降低幅度很大,因此其强度开始明显弱于草地下垫面,而其他下垫面的变化与对流层相差不大。在平流层上层(US),下垫面难以影响,因此曲线较为重合,季节变化性也最弱。推测湍流的产生这一现象的原因还与下垫面对应的植被覆盖率、降水量、土壤水分含量都有关系,具体原因需要进一步的研究。
致谢:感谢郭建平老师提供的程序方法建议。
曹富强, 丹利, 马柱国, 2015. 中国农田下垫面变化对气候影响的模拟研究[J]. 气象学报, 73(1): 128-141. Cao F Q, Dan L, Ma Z G, 2015. Simulative study of the impact of the cropland change on the regional climate over China[J]. Acta Meteor Sin, 73(1): 128-141 (in Chinese).
|
陈德辉, 秦成, Bougeault P, 1996. 一个改进的湍流垂直扩散过程参数化方案[J]. 气象学报, 54(3): 333-347. Chen D H, Qin C, Bougeault P, 1996. A improved parameterization scheme of vertical turbulent diffusion[J]. Acta Meteor Sin, 54(3): 333-347 (in Chinese). DOI:10.3321/j.issn:0577-6619.1996.03.009
|
龚玺, 朱蓉, 李泽椿, 2018. 我国不同下垫面的近地层风切变指数研究[J]. 气象, 44(9): 1160-1168. Gong X, Zhu R, Li Z C, 2018. Study of near-surface wind shear exponents of different regions in China[J]. Meteor Mon, 44(9): 1160-1168 (in Chinese).
|
郝民, 田伟红, 龚建东, 2014. L波段秒级探空资料在GRAPES同化系统中的应用研究[J]. 气象, 40(2): 158-165. Hao M, Tian W H, Gong J D, 2014. Study of L-band second-level radiosonde data applied in GRAPES assimilation system[J]. Meteor Mon, 40(2): 158-165 (in Chinese). DOI:10.3969/j.issn.1001-7313.2014.02.005
|
洪雯, 王毅勇, 2010. 非均匀下垫面大气边界层研究进展[J]. 南京信息工程大学学报(自然科学版), 2(2): 155-161. Hong W, Wang Y Y, 2010. Review of researches on atmospheric boundary layer over heterogeneous underlying surface[J]. J Nanjing Univ Inform Sci Technol (Nat Sci Ed), 2(2): 155-161 (in Chinese).
|
李伟, 赵培涛, 郭启云, 等, 2011. 中国GTS1-2型电子探空仪阳江国际比对结果分析[J]. 气象, 37(11): 1466-1472. Li W, Zhao P T, Guo Q Y, et al, 2011. The analysis of Yangjiang international radiosonde intercomparison results for Chinese GTS1-2 electronic radiosonde[J]. Meteor Mon, 37(11): 1466-1472 (in Chinese). DOI:10.7519/j.issn.1000-0526.2011.11.020
|
刘辉志, 王雷, 杜群, 2018. 大气边界层物理研究进展(2012—2017年)[J]. 大气科学, 42(4): 823-832. Liu H Z, Wang L, Du Q, 2018. An overview of recent studies on atmospheric boundary layer physics (2012-2017)[J]. Chin J Atmos Sci, 42(4): 823-832 (in Chinese).
|
刘明星, 张宏升, 宋星灼, 等, 2008. 不同下垫面温度和湿度湍流谱特征研究[J]. 北京大学学报(自然科学版), 44(3): 391-398. Liu M X, Zhang H S, Song X Z, et al, 2008. Spectral characteristics of atmospheric turbulence over various surface conditions[J]. Acta Sci Nat Univ Pekinensis, 44(3): 391-398 (in Chinese). DOI:10.3321/j.issn:0479-8023.2008.03.011
|
潘乃先, 陈家宜, 栾胜基, 1993. 不同下垫面表面层的湍流度统计特征[J]. 北京大学学报(自然科学版), 29(5): 622-628. Pan N X, Chen J Y, Luan S J, 1993. The statistical characteristics of turbulent intensities in surface layer at different underlying Earth's surfaces[J]. Acta Sci Nat Univ Pekinensis, 29(5): 622-628 (in Chinese). DOI:10.13209/j.0479-8023.1993.080
|
涂钢, 刘辉志, 董文杰, 2009. 半干旱区不同下垫面近地层湍流通量特征分析[J]. 大气科学, 33(4): 719-725. Tu G, Liu H Z, Dong W J, 2009. Characteristics of the surface turbulent fluxes over degraded grassland and cropland in the semi-arid area[J]. Chin J Atmos Sci, 33(4): 719-725 (in Chinese). DOI:10.3878/j.issn.1006-9895.2009.04.06
|
王少影, 张宇, 吕世华, 等, 2010. 应用通量方差法估算戈壁绿洲下垫面湍流通量的研究[J]. 大气科学, 34(6): 1214-1222. Wang S Y, Zhang Y, Lü S H, et al, 2010. Estimation of turbulence fluxes using the flux-variance method over the Gobi and Oasis surfaces[J]. Chin J Atmos Sci, 34(6): 1214-1222 (in Chinese). DOI:10.3878/j.issn.1006-9895.2010.06.14
|
杨湘婧, 徐祥德, 陈宏尧, 等, 2011. L波段探空高分辨率廓线中近地层信息分析及相关模型[J]. 气象, 37(12): 1504-1510. Yang X J, Xu X D, Chen H Y, et al, 2011. The analysis and correlation model of the surface layer information in L-band radiosonde high resolution profile[J]. Meteor Mon, 37(12): 1504-1510 (in Chinese). DOI:10.7519/j.issn.1000-0526.2011.12.005
|
岳平, 张强, 牛生杰, 等, 2012. 半干旱草原下垫面能量平衡特征及土壤热通量对能量闭合率的影响[J]. 气象学报, 70(1): 136-143. Yue P, Zhang Q, Niu S J, et al, 2012. Characters of surface energy balance over a semi-arid grassland and effects of soil heat flux on energy balance closure[J]. Acta Meteor Sin, 70(1): 136-143 (in Chinese).
|
张璐, 黄倩, 张宏昇, 等, 2021. 干湿地表的湍流特征及其对深对流影响的大涡模拟[J]. 气象学报, 79(4): 659-673. Zhang L, Huang Q, Zhang H S, et al, 2021. Large eddy simulation of turbulence effects on deep-convection triggering over dry and wet surfaces[J]. Acta Meteor Sin, 79(4): 659-673 (in Chinese).
|
张蕴帅, 黄倩, 马耀明, 等, 2021. 黄河源区鄂陵湖湖面和湖边草地对流边界层湍流结构特征的大涡模拟研究[J]. 大气科学, 45(2): 435-455. Zhang Y S, Huang Q, Ma Y M, et al, 2021. Large eddy simulation study of the turbulent structure characteristics of the convective boundary layer over Ngoring Lake and surrounding grassland in the source region of the Yellow River[J]. Chin J Atmos Sci, 45(2): 435-455 (in Chinese).
|
Clayson C A, Kantha L, 2008. On turbulence and mixing in the free atmosphere inferred from high-resolution soundings[J]. J Atmos Oceanic Technol, 25(6): 833-852. DOI:10.1175/2007JTECHA992.1
|
Dillon T M, 1982. Vertical overturns: a comparison of Thorpe and Ozmidov length scales[J]. J Geophys Res: Oceans, 87(C12): 9601-9613. DOI:10.1029/JC087iC12p09601
|
Durran D R, Klemp J B, 1982. On the effects of moisture on the Brunt-Väisälä frequency[J]. J Atmos Sci, 39(10): 2152-2158. DOI:10.1175/1520-0469(1982)039<2152:OTEOMO>2.0.CO;2
|
Dutta G, Ajay Kumar M C, Vinay Kumar P, et al, 2009. High resolution observations of turbulence in the troposphere and lower stratosphere over Gadanki[J]. Ann Geophys, 27(6): 2407-2415. DOI:10.5194/angeo-27-2407-2009
|
Ferron B, Mercier H, Speer K, et al, 1998. Mixing in the Romanche Fracture Zone[J]. J Phys Oceanogr, 28(10): 1929-1945. DOI:10.1175/1520-0485(1998)028<1929:MITRFZ>2.0.CO;2
|
Fritts D C, Garten J F, Andreassen ø, 1996. Wave breaking and transition to turbulence in stratified shear flows[J]. J Atmos Sci, 53(8): 1057-1085. DOI:10.1175/1520-0469(1996)053<1057:WBATTT>2.0.CO;2
|
Fritts D C, Wan K M, Franke P M, et al, 2012. Computation of clear-air radar backscatter from numerical simulations of turbulence: 3.Off-zenith measurements and biases throughout the lifecycle of a Kelvin-Helmholtz instability[J]. J Geophys Res: Atmos, 117(D17): D17101.
|
Fritts D C, Wang L, Geller M A, et al, 2016. Numerical modeling of multiscale dynamics at a high Reynolds number: instabilities, turbulence, and an assessment of Ozmidov and Thorpe scales[J]. J Atmos Sci, 73(2): 555-578. DOI:10.1175/JAS-D-14-0343.1
|
Galbraith P S, Kelley D E, 1996. Identifying overturns in CTD profiles[J]. J Atmos Oceanic Technol, 13(3): 688-702. DOI:10.1175/1520-0426(1996)013<0688:IOICP>2.0.CO;2
|
Gargett A, Garner T, 2008. Determining thorpe scales from ship-lowered CTD density profiles[J]. J Atmos Oceanic Technol, 25(9): 1657-1670. DOI:10.1175/2008JTECHO541.1
|
Gerz T, Holzäpfel F, Bryant W, et al, 2005. Research towards a wake-vortex advisory system for optimal aircraft spacing[J]. C R Phys, 6(4-5): 501-523. DOI:10.1016/j.crhy.2005.06.002
|
Guo J P, Li Y, Cohen J B, et al, 2019. Shift in the temporal trend of boundary layer height in China using long-term (1979-2016) radiosonde data[J]. Geophys Res Lett, 46(11): 6080-6089. DOI:10.1029/2019GL082666
|
Guo J P, Liu H, Li Z Q, et al, 2018. Aerosol-induced changes in the vertical structure of precipitation: a perspective of TRMM precipitation radar[J]. Atmos Chem Phys, 18(18): 13329-13343. DOI:10.5194/acp-18-13329-2018
|
Guo J P, Miao Y C, Zhang Y, et al, 2016. The climatology of planetary boundary layer height in China derived from radiosonde and reanalysis data[J]. Atmos Chem Phys, 16(20): 13309-13319. DOI:10.5194/acp-16-13309-2016
|
Guo J P, Zhai P M, Wu L, et al, 2014. Diurnal variation and the influential factors of precipitation from surface and satellite measurements in Tibet[J]. Int J Climatol, 34(9): 2940-2956. DOI:10.1002/joc.3886
|
Jaeger E B, Sprenger M, 2007. A Northern Hemispheric climatology of indices for clear air turbulence in the tropopause region derived from ERA40 reanalysis data[J]. J Geophys Res: Atmos, 112(D20): D20106. DOI:10.1029/2006JD008189
|
Ko H C, Chun H Y, Wilson R, et al, 2019. Characteristics of atmospheric turbulence retrieved from high vertical-resolution radiosonde data in the United States[J]. J Geophys Res: Atmos, 124(14): 7553-7579. DOI:10.1029/2019JD030287
|
Li Q, Rapp M, Schrön A, et al, 2016. Derivation of turbulent energy dissipation rate with the Middle Atmosphere Alomar Radar System (MAARSY) and radiosondes at Andøya, Norway[J]. Ann Geophys, 34(12): 1209-1229. DOI:10.5194/angeo-34-1209-2016
|
Li Z Q, Lau W K M, Ramanathan V, et al, 2016. Aerosol and monsoon climate interactions over Asia[J]. Rev Geophys, 54(4): 866-929.
|
Liu X, Xu J Y, Yuan W, 2014. Diurnal variations of turbulence parameters over the tropical oceanic upper troposphere during SCSMEX[J]. Sci China Technol Sci, 57(2): 351-359. DOI:10.1007/s11431-013-5445-5
|
Liu X D, Bai A J, Liu C H, 2009. Diurnal variations of summertime precipitation over the Tibetan Plateau in relation to orographically-induced regional circulations[J]. Environ Res Lett, 4(4): 045203.
|
Luce H, Wilson R, Dalaudier F, et al, 2014. Simultaneous observations of tropospheric turbulence from radiosondes using Thorpe analysis and the VHF MU radar[J]. Radio Sci, 49(11): 1106-1123.
|
Lv Y M, Guo J P, Li J, et al, 2021. Spatiotemporal characteristics of atmospheric turbulence over China estimated using operational high-resolution soundings[J]. Environ Res Lett, 16(5): 054050.
|
Storer L N, Williams P D, Gill P G, 2019. Aviation turbulence: dynamics, forecasting, and response to climate change[J]. Pure Appl Geophys, 176(5): 2081-2095.
|
Sunilkumar S V, Muhsin M, Parameswaran K, et al, 2015. Characteristics of turbulence in the troposphere and lower stratosphere over the Indian Peninsula[J]. J Atmos Sol-Terr Phys, 133: 36-53.
|
Thorpe S A, 1977. Turbulence and mixing in a Scottish Loch[J]. Phil Trans Roy Soc Lond A, 286(1334): 125-181.
|
Wilson R, Dalaudier F, Luce H, 2011. Can one detect small-scale turbulence from standard meteorological radiosondes?[J]. Atmos Meas Tech, 4(5): 795-804.
|
Wilson R, Luce H, Dalaudier F, et al, 2010. Turbulence patch identification in potential density or temperature profiles[J]. J Atmos Oceanic Technol, 27(6): 977-993.
|
Wilson R, Luce H, Hashiguchi H, et al, 2013. On the effect of moisture on the detection of tropospheric turbulence from in situ measurements[J]. Atmos Meas Tech, 6(3): 697-702.
|
Wilson R, Luce H, Hashiguchi H, et al, 2014. Energetics of persistent turbulent layers underneath mid-level clouds estimated from concurrent radar and radiosonde data[J]. J Atmos Sol-Terr Phys, 118: 78-89.
|
Zhang J, Zhang S D, Huang C M, et al, 2019a. Latitudinal and topographical variabilities of free atmospheric turbulence from high-resolution radiosonde data sets[J]. J Geophys Res: Atmos, 124(8): 4283-4298.
|
Zhang J, Zhang S D, Huang C M, et al, 2019b. Statistical study of atmospheric turbulence by Thorpe analysis[J]. J Geophys Res: Atmos, 124(6): 2897-2908.
|
Zhang J Q, Chen H B, Li Z Q, et al, 2010. Analysis of cloud layer structure in Shouxian, China using RS92 radiosonde aided by 95 GHz cloud radar[J]. J Geophys Res: Atmos, 115(D7): D00K30.
|
 2023, Vol. 49
2023, Vol. 49 
