中国位于东亚季风区域,受气候特征、地形环境等因素影响,气象灾害频发。大风灾害作为中国的主要灾害性天气之一,每年都会造成重大经济损失,同时给人民出行安全和社会活动带来严重影响,因此加强大风灾害的预报预警服务对保障人民生命财产安全至关重要(张庆云等,2008)。
目前近地面风速的预报方法主要以统计预报和数值天气预报为主。统计预报方法是根据历史观测数据,通过分析总结数据序列之间的规律或构建统计模型对未来风速进行预报;数值天气预报方法主要基于大气运动方程,构建物理模型来进行预报(杨程等,2019)。统计预报方法主要包括时间序列法(Bossanyi,1985)、持续法(Alexiadis et al,1998)和空间相关法(Barbounis et al,2006)等,但是统计预报方法过度依赖历史观测数据且预报时效性较短,数值预报方法考虑了较多的物理和动力过程,其预报时效较长,可以更好地满足精细化预报服务需求(孙川永等,2009)。伴随数值天气预报模式的不断发展与成熟,MM5(Mesoscale Model 5)和WRF(Weather Research and Forecasting Model)等中尺度数值模式开始广泛应用于风速预报中(李晓莉等,2005),除此之外,美国的eWind(Petersen,1999)和德国的Previento(Yu et al,2006)等数值模式也相继被开发并重点应用于风预报研究领域。
然而数值模式存在物理参数化方案不完善、地形不够精确等问题,导致其预报结果的准确性随时效的增加而降低,可以通过订正方法来提高模式预报精度。常用的风速订正方法有高斯统计预报方法(Monahan,2013)、回归订正方法(Rozas-Larraondo et al,2014;申华羽等,2020)、MOS预报法(荣艳敏等,2015)、集合订正方法(胡海川等,2017)和人工智能订正方法(张颖超等,2016;孙全德等,2019;王在文等,2019)。对于给定分辨率的区域数值模式而言,模式地形和实际地形不匹配是导致地面风速预报值与观测值存在较大误差的重要因子(贺皓,1995),模式地形经过平滑处理后与真实地形存在差异,而模式的风速预报是位于模式地形高度上的预报诊断量,不准确的模式地形会严重影响地面风速的预报效果。基于此,需要对数值模式的地面风速预报结果进行偏差订正,以确保预报值与观测值更加接近,例如基于模式预报的风速及实况观测的阵风风速历史资料建立联合概率密度分布函数,通过概率密度匹配法对WRF模式的极大风速进行订正(钱磊等,2019)。上述风速订正方法依赖于长期连续稳定的数值预报和观测数据历史样本,在实际应用中受到较大限制。而莫宁和奥布霍夫提出的莫宁-奥布霍夫(Monin-Obukhov)相似理论为近地层的大气特征分析研究奠定基础,莫宁-奥布霍夫相似理论表明近地面层可被当作为常通量层,在此基础上可以描述出近地面层的大气湍流特征(苗曼倩等,1987),即表明地面以上某一高度的风速和地形高度、地面粗糙度以及地表风速通量相关。相似理论被认为是成熟的理论方法(苗曼倩等,1997;Barthelmie,2001),但目前该理论还未应用于地面风速的偏差订正。由上述可知,模式地形和实际地形不匹配是导致地面风速预报与观测存在差异的重要因素,因此本文基于相似理论构建风速预报偏差订正方案,主要解决地形高度差导致的预报偏差问题,该订正方案不需要历史样本且计算快捷。
1 数据和方法地面风速预报是在考虑模式最低层高度和模式地形高度的基础上利用模式最低层风速预报值计算的诊断量,而模式与实际地形差异会导致地面风速诊断预报的结果与风速观测值产生偏差。实况地面风速是地面之上10 m高度的风速观测值,而基于相似理论的偏差订正方案主要降低地形差异对风速预报的影响,因此:当观测站点高度和模式地形高度差值小于10 m时,则认为地形差对风速预报偏差影响较小,不对该站点风速预报进行订正;而当两者的地形高度差超过10 m阈值时, 利用上述方案对地面风速预报进行订正。
1.1 偏差订正方案基于相似理论可推知地面以上高度h1处的风速U1(Barthelmie,2001):
| $ U_1=\frac{U^*}{k} \ln \left(\frac{h_1}{z_0}\right) $ | (1) |
式中:k为常数,z0为地面粗糙度,U*为地面摩擦速度。此外大气层结状态同样会对风速的垂直变化产生影响,大气层结包括稳定、中性和不稳定状态,而式(1)只满足中性大气层结状态下的风速垂直变化情况(Stull,1988),大气处于稳定或不稳定状态时,式(1)对于风速的垂直变化特征描述不准确。因此在式(1)中加入大气稳定度的判定项Ψ(τ)(苗曼倩等,1987),将式(1)变换为式(2):
| $ U_1=\frac{U^*}{k}\left[\ln \left(\frac{h_1}{z_0}\right)-\varPsi(\tau)\right] $ | (2) |
式中:Ψ(τ)是τ的函数关系式。
| $ \tau=\frac{h}{L} $ | (3) |
式中:h为高度,L为莫宁-奥布霍夫长度, 可直接从数值模式中获取,根据式(3)可以得出不同高度h1和h2上的风速U1与U2有以下关系:
| $ \frac{U_2}{U_1}=\frac{\ln \left(h_2 / z_0\right)-\varPsi(\tau)}{\ln \left(h_1 / z_0\right)-\varPsi(\tau)} $ | (4) |
当大气处于不稳定(τ < 0)状态下时(Paulson,1970):
| $ \left\{\begin{array}{l} \varPsi(\tau)=2 \ln \left(\frac{1+x}{2}\right)+\ln \left(\frac{1+x^2}{2}\right)- \\ \quad\quad\quad\quad\quad 2 \arctan (x)+\frac{\pi}{2} \\ x=(1-15 \tau)^{1 / 4} \end{array}\right. $ | (5) |
而大气处于稳定(τ≥0)状态下:
| $ \varPsi(\tau)=-4.7 \tau $ | (6) |
数值模式中地面风速是位于模式地形高度的预报值,而模式地形与实际地形高度通常不一致,因此需要将风速预报由数值模式的地形高度订正到实际地形高度。根据式(4)可得出:
| $ \left\{\begin{array}{l} U_{\mathrm{o}}=U_{\mathrm{m}} \varepsilon \\ \varepsilon=\frac{\ln \left(h_{\mathrm{o}} / z_{\mathrm{m}}\right)-\varPsi(\tau)}{\ln \left(h_{\mathrm{m}} / z_{\mathrm{m}}\right)-\varPsi(\tau)} \end{array}\right. $ | (7) |
式中:Uo为订正后的10 m风速值,Um为数值模式的10 m风速预报值,zm为数值模式中地面粗糙度。ho和hm为实际地形高度和对应点的模式地形高度,ε为偏差订正系数。基于式(7)构建的订正方案适用于拥有高度观测值的站点的风速预报偏差订正, 需要指出的是偏差订正方案中采用的大气稳定度项Ψ(τ)由数值模式背景场所决定。
成熟的相似理论研究指出风速垂直变化特征在近地面符合对数率变化(Stull,1988;贺千山和毛节泰, 2005),当数值模式地形和实际地形差值(ho和hm差)较大时,需对偏差订正系数ε进行适当调整:
| $ \varepsilon= \begin{cases}\frac{\ln \left(h_{\mathrm{o}} / z_{\mathrm{m}}\right)-\varPsi(\tau)}{\ln \left[\left(h_{\mathrm{o}}+h_{\mathrm{sfc}}\right) / z_{\mathrm{m}}\right]-\varPsi(\tau)} & h_{\mathrm{m}}>h_{\mathrm{o}} \\ \frac{\ln \left[\left(h_{\mathrm{m}}+h_{\mathrm{sfc}}\right) / z_{\mathrm{m}}\right]-\varPsi(\tau)}{\ln \left(h_{\mathrm{m}} / z_{\mathrm{m}}\right)-\varPsi(\tau)} & h_{\mathrm{m}}<h_{\mathrm{o}}\end{cases} $ | (8) |
式中:hsfc为近地层高度。近地层高度受下垫面和大气层结状态影响而不同,一般情况下可选取为边界层高度的十分之一(Stull,1988),而边界层高度可由数值模式的背景场通过理查森数Ri计算得到,公式如下(张碧辉等,2012):
| $ R i=\frac{g\left(\Delta z \Delta \theta_{\mathrm{o}}\right)}{\Delta U \Delta \theta_{\mathrm{vo}}} $ | (9) |
式中:g是重力加速度,Δz是模式K层与模式最低层之间的垂直距离,Δθo、ΔU和Δθvo分别是位温、平均速度和虚位温在垂直方向上的差值。Ri>0时的Δz即为模式边界层高度。
1.2 模式设置本文选取的数值天气预报模式为北京城市气象研究院研发的快速更新多尺度分析及预报-短期预报系统(Rapid-Refresh Multi-Scale Analysis and Prediction System-Short Term,RMAPS-ST)。该数值模式采用两重嵌套设计,如图 1a所示,外区(D01)分辨率为9 km,覆盖全国范围,内区(D02, 图 1c所示)分辨率为3 km,覆盖华北地区,垂直层数均为59层,模式层顶高为10 hPa(张鑫宇等,2021)。采用0.25°的ECMWF细网格资料作为模式的驱动场,模式选取YSU边界层方案和Thompson微物理方案,长波和短波辐射方案都选RRTMG方案,外区积云选取新的Tiedtke方案,内区不开启积云方案。
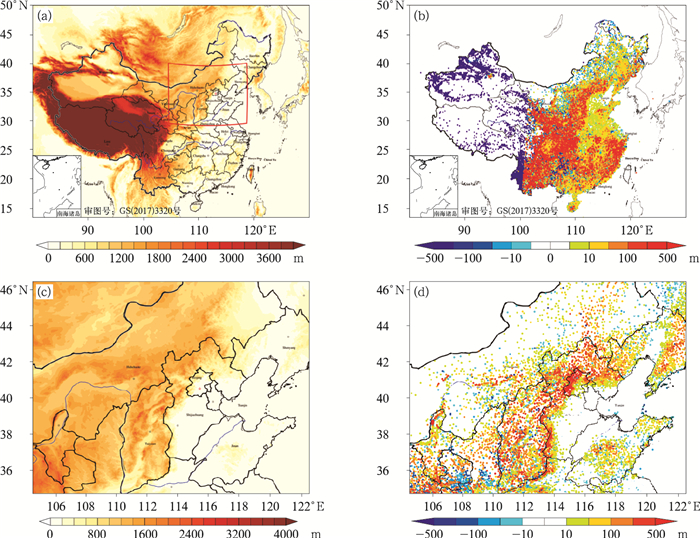
|
图 1 模式(a, b)外区,(c, d)内区(a,c)不同区域地形高度及(b,d)模式地形减去实际地形的高度差值 Fig. 1 (a, c) Terrain height in (a, b) D01, (c, d) D02 of the model and (b, d) terrain height difference between the model and the observation |
模式外区采用分辨率为2′的地形数据,内区采用30″的地形数据,然后通过模式的预处理模块将地形数据插值到模式设定的网格区域。数值模式无法有效地对次网格地形进行解析, 因此模式地形与实际地形存在偏差。我国地形呈现西高东低的分布特征(图 1a),由西向东模式的地形呈阶梯式下降,同时根据获取的全国2400多个自动气象站的高度信息得出各站点模式地形和实际地形的高度差(图 1b),全国大多数区域内的模式地形均要高于实际地形,73.4%的站点所在位置的模式地形更高,我国西部和北部地区的模式地形明显偏低,而河北地区及浙江等地的地形高度差较小,对于华北区域(模式内区) 760多个站点而言, 51.8%的观测站点所对应的模式地形偏高。模式外区中82%的站点所在位置的模式地形与实际地形高度差在100 m范围内,而由于模式内区分辨率提高,因此插值到站点后的模式地形与实际地形更加接近,内区地形高度差在100 m范围内的站点占比为96%,模式地形最大偏高约240 m,最大偏低约390 m。
2 偏差订正方案效果评估RMAPS-ST主要支撑华北地区的短期精细化天气预报和气象服务,因此重点分析模式内区的风速预报及其偏差订正效果。设计两组试验,控制试验(CTRL)的风速预报值为模式直接预报结果,敏感性试验(BASE)的风速预报值是基于偏差订正方案改进后的结果。00时(世界时,下同)起始预报的数值模式采用热启动方式运行,即00时采用区域模式前一天18时起始预报的6 h预报结果作为同化所需的背景场,同化多源资料后进行积分预报。
2.1 风速预报偏差的空间分布为避免个例分析的偶然性,验证订正方案的普适性,并考虑冬、夏不同季节风速预报的差异,基于表1的试验设计选取2021年7月1—15日以及12月1—15日各15 d的批量试验结果进行分析。图 2是7月(图 2a,2b)和12月(图 2c,2d)各15 d的平均结果,对华北区域而言,6 h预报以正偏差为主,一般情况下风速随高度上升而增大(申华羽等,2009),由于华北区域模式地形高于观测地形,因此模式在进行10 m风诊断预报时偏高。7月和12月的6 h预报平均偏差分别为0.87 m·s-1和0.69 m·s-1,使用订正方案后偏差可分别降低为0.60 m·s-1和0.38 m·s-1,降幅分别为20.7%和36.7%。华北区域内订正后风速有明显变化(差值≥0.1 m·s-1)的站点数有320个以上,其中70%的站点订正效果变优,且订正幅度较大,30%站点效果变差。
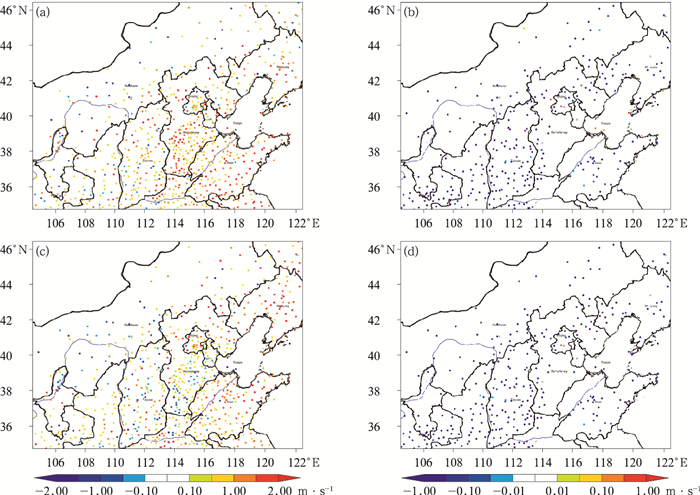
|
图 2 2021年(a, b)7月1—15日,(c, d)12月1—15日模式6 h风速预报和实况(OBS)偏差的空间分布 (a,c)CTRL-OBS,(b,d)BASE-CTRL Fig. 2 Spatial distribution of deviation between 6 h wind speed forecast and observation (OBS) in (a, b) 1-15 July and (c, d) 1-15 December 2021 (a, c) CTRL-OBS, (b, d) BASE-CTRL |
对上述两个时段内的24 h预报进行分析,图 3是全区所有站点的平均值,明显看出无论夏季还是冬季风速预报值均有所高估,使用订正方案后24 h内的风速预报与观测更加接近,尤其是前12 h的订正效果明显,7月前12 h的风速观测(OBS)平均值为2.57 m·s-1,订正后风速预报值由3.55 m·s-1下降为3.29 m·s-1,而12月对应的风速观测值、预报值和预报订正值则分别为2.53、3.43和3.19 m·s-1,使用订正方案后预报准确率明显提升。
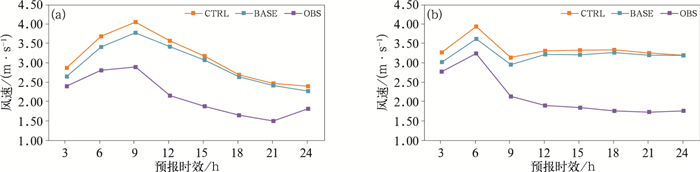
|
图 3 2021年(a)7月1—15日,(b)12月1—15日订正前、后风速预报和观测的平均值 Fig. 3 Average values of wind speed forecast and observation in (a) 1-15 July and (b) 1-15 December 2021 |
夏季24 h内风速预报偏差呈现单峰变化,而冬季风速预报的平均偏差变化在12 h后基本维持稳定(图 4)。夏季24 h内风速的平均偏差(Bias)和均方根误差(RMSE)分别为0.97 m·s-1和1.33 m·s-1,订正后Bias和RMSE分别下降15.5%和4.5%,前12 h预报的订正效果更明显,Bias降幅为23.5%,RMSE降幅为6.8%。对应的冬季24 h Bias和RMSE分别为1.20 m·s-1和1.51 m·s-1,订正后两项指标分别降低10.8%和5.3%,同样前12 h订正幅度更大,Bias和RMSE分别降低23.3%和7.9%。无论冬季还是夏季订正方案可以有效降低风速预报偏差。
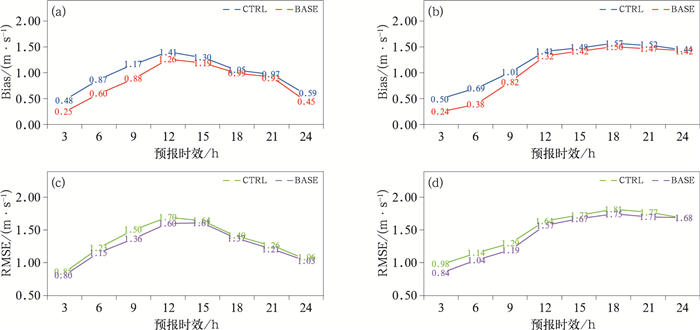
|
图 4 2021年(a, c)7月1—15日,(b, d)12月1—15日订正前、后风速预报的(a, b)偏差(Bias)及(c, d)均方根误差(RMSE) Fig. 4 (a, b) Bias and (c, d) RMSE of wind speed forecast and observation in (a, c) 1-15 July and (b, d) 1-15 December 2021 |
上文将偏差订正方案耦合到模式中运行,因此统计结果包括内区所有站点,而内区参与评估的760多个站点中有58.5%的站点所在位置的地形高度差异小于10 m阈值,并没有对其预报结果进行订正,因此基于全区所有站点的统计结果更多是说明订正方案对于数值模式的整体贡献。图 5给出偏差订正方案产生实际效果的320多个站点预报的统计,该结果直接表明方案本身的实际应用效果。由图 5a可知12 h内平均风速预报Bias可以降低50%以上,24 h内Bias降幅可达27%以上,夏季风速预报的订正效果相对更优。同样,图 5b可见,12 h和24 h的风速预报RMSE分别降低17%和11%以上,说明偏差订正方案对于地面站点风速预报起到非常显著的正面效果。
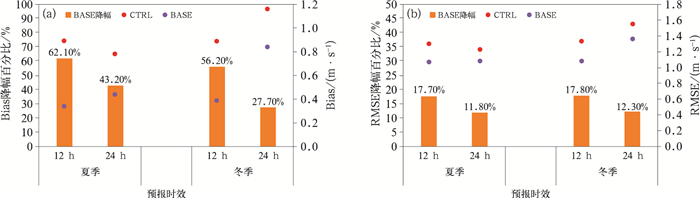
|
图 5 冬季(2021年12月1—15日)和夏季(7月1—15日)订正方案的实际效果 (a)偏差及其降幅,(b)均方根误差及其降幅 Fig. 5 Actual effect of correction scheme in winter (1-15 December) and summer (1-15 July) of 2021 (a) Bias and Bias reduction of BASE test, (b) RMSE and its reduction of BASE test |
根据相似理论,在不考虑Ψ(τ)的情况下,近地面风速随高度增高而变大,因此(在相似理论适用范围内)理论上模式地形高于实际地形时,风速预报值偏高,反之亦然。但是图 6a为夏季CTRL试验00时起始预报,06时和18时的风速预报偏差随地形高度差的变化。无论模式地形比观测地形偏高还是偏低,大部分站点的风速预报均偏高,说明模式的地面风速预报偏差不仅仅是地形高度差所造成的。由图 6b和6c可以看出,预报偏差为正的站点预报效果改善明显,除少数站点外,大部分预报偏差为负的站点预报并没有进一步加剧,说明偏差订正方案依据理论可以很好地对图 6a中第二和第四象限中的站点预报进行订正,同时在订正方案中引入稳定度相关性Ψ(τ)和hsfc,可以改善图 6a第三象限中大多数站点的预报,并且有效降低图 6a第一象限中站点预报偏差订正的负效果。对于多数站点而言,应用订正方案会降低站点的风速预报偏差。
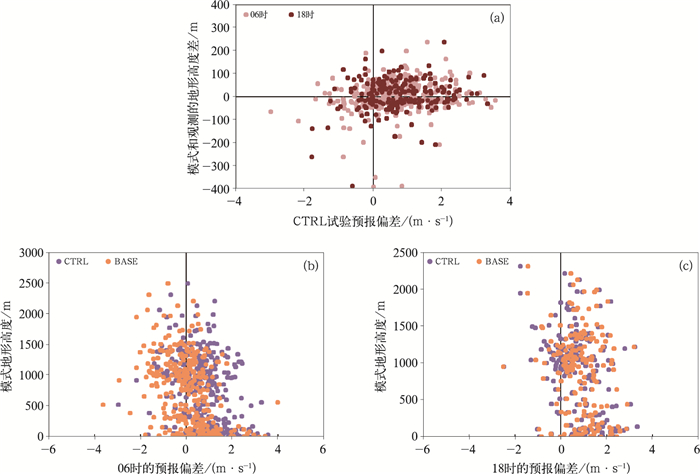
|
图 6 2021年7月1—15日模式高度差对订正方案的影响 (a)预报偏差随地形高度差的变化,(b,c)不同试验的预报值随模式地形高度的变化 Fig. 6 Impact of model height difference on correction scheme (a) variation of prediction deviation with terrain height difference, (b, c) variation of prediction values of different tests with model terrain height in 1-15 July 2021 |
而对比图 6b和6c可以看出,方案应用在06时的订正力度更大,说明订正系数不是固定不变的。对于同一个站点而言,地形高度差是一定的,但不同预报时效的订正系数随Ψ(τ)的变化而改变,当大气层结处于不稳定状态时,利用式(5)得出Ψ(τ)为正,反之大气处于稳定状态时Ψ(τ)为负,因此结合式(7)可以看出处于不稳定状态下的站点预报订正系数比其处于稳定状态时偏小。
3 结论与讨论基于莫宁-奥布霍夫相似理论建立地面10 m风速预报偏差订正方案,旨在降低模式和实际地形差异对风速预报偏差的影响,同时在订正方案中引入大气稳定度影响因子,考虑大气层结状态对于预报偏差的影响。该订正方案不需要大量历史观测样本且计算快捷,通过2021年夏季和冬季各15 d的模式预报结果的对比分析,可得出以下结论:
(1) 将订正方案嵌套到RMAPS-ST模式中,统计内区所有站点的预报结果发现,12 h内风速预报的平均偏差和均方根误差分别可以降低20%和8%左右,24 h内可分别降低10%和5%左右。
(2) 订正方案对地形差小于10 m阈值的站点预报不进行任何处理,因此针对内区320多个地形高度差大于10 m的观测站点进行分析,应用订正方案后12 h和24 h的平均风速预报偏差可分别降低50%和27%以上,均方根误差可分别降低17%和11%以上。
(3) 订正方案对24 h预报的地面风速预报均有正贡献,且前12 h预报的订正效果明显更优。订正方案中考虑大气稳定度后,订正系数会随着大气稳定度条件而变化,因此同一站点不同时刻的预报偏差订正幅度是不同的。
上述地面风速偏差订正方案依赖于实际地形高度,地面观测站具有实际高度观测值,因此该方案适用于订正插值到观测站点位置的风速预报,而由于数值模式没有对应的实际地形高度网格数据,因此该订正方案暂时还不能对数值模式的格点预报进行偏差订正。此外,订正方案中使用的地面粗糙度数值是根据模式的下垫面类型对照查表得出,而复杂的下垫面对模式地面风速预报同样有较大影响(薛文博等,2020),因此对于某些观测站点而言,对应模式点的下垫面类型与实际下垫面类型相差较大时,可能会影响偏差订正方案的效果。但整体而言应用订正方案后,地面风速预报准确性有明显提升。
贺皓, 1995. 数值预报产品系统性误差的客观订正[J]. 高原气象, 14(2): 198-206. He H, 1995. Objective correction of systematical error of numerical forecast products[J]. Plateau Meteor, 14(2): 198-206 (in Chinese).
|
贺千山, 毛节泰, 2005. 北京城市大气混合层与气溶胶垂直分布观测研究[J]. 气象学报, 63(3): 374-384. He Q S, Mao J T, 2005. Observation of urban mixed layer at Beijing using a micro pulse lidar[J]. Acta Meteor Sin, 63(3): 374-384 (in Chinese).
|
胡海川, 黄彬, 魏晓琳, 2017. 我国近海洋面10 m风速集合预报客观订正方法[J]. 气象, 43(7): 856-862. Hu H C, Huang B, Wei X L, 2017. Objective correction method of ensemble forecast of 10 m winds on Chinese offshore[J]. Meteor Mon, 43(7): 856-862 (in Chinese).
|
李晓莉, 毕宝贵, 李泽椿, 2005. 北京冬季城市边界层结构形成机制的初步数值研究[J]. 气象学报, 63(6): 889-902. Li X L, Bi B G, Li Z C, 2005. Simulation study of formation mechanism of winter urban boundary layer structure over Beijing Area[J]. Acta Meteor Sin, 63(6): 889-902 (in Chinese). DOI:10.3321/j.issn:0577-6619.2005.06.006
|
苗曼倩, 赵鸣, 王彦昌, 等, 1987. 近地层湍流通量计算及几种塔层风廓线模式的研究[J]. 大气科学, 11(4): 420-429. Miao M Q, Zhao M, Wang Y C, et al, 1987. The calculation of the turbulent fluxes in surface boundary layer and the study of several models of wind profiles in the tower layer[J]. Sci Atmos Sin, 11(4): 420-429 (in Chinese). DOI:10.3878/j.issn.1006-9895.1987.04.11
|
苗曼倩, 朱超群, 季劲钧, 1997. 近地层相似理论适用的分析研究[J]. 气象学报, 55(2): 210-218. Miao M Q, Zhu C Q, Ji J J, 1997. Study on the applicability of the surface layer similarity theory[J]. Acta Meteor Sin, 55(2): 210-218 (in Chinese).
|
钱磊, 邱学兴, 郑淋淋, 2019. 基于概率密度匹配方法的WRF模式阵风风速误差订正[J]. 气象科技, 47(6): 916-926. Qian L, Qiu X X, Zheng L L, 2019. Error correction of WRF model gust speed based on probability density function matching method[J]. Meteor Sci Technol, 47(6): 916-926 (in Chinese).
|
荣艳敏, 阎丽凤, 盛春岩, 等, 2015. 山东精细化海区风的MOS预报方法研究[J]. 海洋预报, 32(3): 59-67. Rong Y M, Yan L F, Sheng C Y, et al, 2015. A study on MOS forecasting method of gale wind in Shandong Coast[J]. Mar For, 32(3): 59-67 (in Chinese).
|
申华羽, 方艳莹, 涂小萍, 等, 2020. ECMWF细网格10m风预报在浙江沿海的评估与订正[J]. 气象, 46(11): 1485-1494. Shen H Y, Fang Y Y, Tu X P, et al, 2020. Verification of ECMWF 10 m wind forecast for coastal Zhejiang Province[J]. Meteor Mon, 46(11): 1485-1494 (in Chinese).
|
申华羽, 吴息, 谢今范, 等, 2009. 近地层风能参数随高度分布的推算方法研究[J]. 气象, 35(7): 54-60. Shen H Y, Wu X, Xie J F, et al, 2009. Research on algorithm of wind energy parameters in surface layer with height[J]. Meteor Mon, 35(7): 54-60 (in Chinese).
|
孙川永, 陶树旺, 罗勇, 等, 2009. 高分辨率中尺度数值模式在风电场风速预报中的应用[J]. 太阳能学报, 30(8): 1097-1099. Sun C Y, Tao S W, Luo Y, et al, 2009. The application of high resolution mesoscale model in wind speed forecasting in wind farm[J]. Acta Energ Solar Sin, 30(8): 1097-1099 (in Chinese).
|
孙全德, 焦瑞莉, 夏江江, 等, 2019. 基于机器学习的数值天气预报风速订正研究[J]. 气象, 45(3): 426-436. Sun Q D, Jiao R L, Xia J J, et al, 2019. Adjusting wind speed prediction of numerical weather forecast model based on machine learning methods[J]. Meteor Mon, 45(3): 426-436 (in Chinese).
|
王在文, 陈敏, Monache L D, 等, 2019. 相似集合预报方法在北京区域地面气温和风速预报中的应用[J]. 气象学报, 77(5): 869-884. Wang Z W, Chen M, Monache L D, et al, 2019. Application of analog ensemble method to surface temperature and wind speed prediction in Beijing Area[J]. Acta Meteor Sin, 77(5): 869-884 (in Chinese).
|
薛文博, 余晖, 汤胜茗, 等, 2020. 上海快速更新同化数值预报系统(SMS-WARR)的近地面风速预报检验评估[J]. 气象, 46(12): 1529-1542. Xue W B, Yu H, Tang S M, et al, 2020. Verification on surface wind speed forecast of Shanghai Meteorological Service-WRF ADAS rapid refresh system (SMS-WARR)[J]. Meteor Mon, 46(12): 1529-1542 (in Chinese).
|
杨程, 姜瑜君, 余贞寿, 等, 2019. 基于偏最小二乘回归的区域换式风速预报订正技术研究[J]. 气象, 45(5): 676-684. Yang C, Jiang Y J, Yu Z S, et al, 2019. Correction technology of regional wind speed forecasting based on partial least square regression[J]. Meteor Mon, 45(5): 676-684 (in Chinese).
|
张碧辉, 刘树华, Liu H P, 等, 2012. MYJ和YSU方案对WRF边界层气象要素模拟的影响[J]. 地球物理学报, 55(7): 2239-2248. Zhang B H, Liu S H, Liu H P, et al, 2012. The effect of MYJ and YSU schemes on the simulation of boundary layer meteorological factors of WRF[J]. Chin J Geophys, 55(7): 2239-2248 (in Chinese).
|
张庆云, 陶诗言, 彭京备, 2008. 我国灾害性天气气候事件成因机理的研究进展[J]. 大气科学, 32(4): 815-825. Zhang Q Y, Tao S Y, Peng J B, 2008. The studies of meteorological disasters over China[J]. Chin J Atmos Sci, 32(4): 815-825 (in Chinese).
|
张鑫宇, 陈敏, 孙娟珍, 等, 2021. WRF-DA中地面观测资料同化方案的改进与应用[J]. 气象学报, 79(1): 104-118. Zhang X Y, Chen M, Sun J Z, et al, 2021. Improvement and application of the ground observation data assimilation scheme in WRF-DA[J]. Acta Meteor Sin, 79(1): 104-118 (in Chinese).
|
张颖超, 肖寅, 邓华, 2016. 基于ELM的风电场短期风速订正技术研究[J]. 气象, 42(4): 466-471. Zhang Y C, Xiao Y, Deng H, 2016. Modification technology research of short-term wind speed in wind farm based on ELM method[J]. Meteor Mon, 42(4): 466-471 (in Chinese).
|
Alexiadis M C, Dokopoulos P S, Sahsamanoglou H S, et al, 1998. Short-term forecasting of wind speed and related electrical power[J]. Solar Energy, 63(1): 61-68.
|
Barbounis T G, Theocharis J B, Alexiadis M C, et al, 2006. Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE Trans Energy Convers, 21(1): 273-284.
|
Barthelmie R J, 2001. Evaluating the impact of wind induced roughness change and tidal range on extrapolation of offshore vertical wind speed profiles[J]. Wind Energ, 4(3): 99-105.
|
Bossanyi E A, 1985. Short-term wind prediction using Kalman filters[J]. Wind Energ, 9(1): 1-8.
|
Monahan A H, 2013. The Gaussian statistical predictability of wind speeds[J]. J Climate, 26(15): 5563-5577.
|
Paulson C A, 1970. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer[J]. J Appl Meteor, 9(6): 857-861.
|
Petersen E L, 1999. 1999 European Wind Energy Conference: Wind Energy for the Next Millennium[M].
London: Routledge Publishers: 1244.
|
Rozas-Larraondo P, Inza I, Lozano J A, 2014. A method for wind speed forecasting in airports based on nonparametric regression[J]. Wea Forecasting, 29(6): 1332-1342.
|
Stull R B, 1988. An Introduction to Boundary Layer Meteorology[M].
London: Kluwer Academic Publishers: 688.
|
Yu W, Benoit R, Girard C, et al, 2006. Wind Energy Simulation Toolkit (WEST): a wind mapping system for use by the wind-energy industry[J]. Wind Energ, 30(1): 15-33.
|
 2023, Vol. 49
2023, Vol. 49 