雾-霾天气一直是人们关注的焦点、研究的热点和政府治理大气污染的重点。雾-霾天气形成的条件主要有两个:一是人类活动向大气中排放的污染物,为霾的形成提供物质条件;二是静稳的气象条件。在污染源基本稳定的前提下,空气质量的优劣主要由气象条件决定。
Ding and Liu(2014)、江琪等(2017)、蔡子颖等(2017)、尚可等(2016)、于文金等(2016)、梅梅等(2019)等对气象条件与空气污染关系的研究表明:空气污染浓度与边界层内多个气象要素显著相关,70%的引起空气污染浓度日均值波动的因素是气象条件的变化。在环境气象服务中需要建立综合表达空气污染气象条件的量化指标,用于预测和评估污染气象条件的长、中、短期变化。国外,Wang and Angell(1999)通过对日平均海平面气压、地转风速、500 hPa日平均水平风速、850 hPa及以下逆温情况等设定判别条件定义了静稳天气指数;Tai et al(2010)基于上文静稳天气的定义,统计分析了美国在大气静稳日和非静稳日PM2.5浓度的差别。该静稳天气指数给出的是大气静稳的定性判断依据,无法满足我国环境气象业务对定量描述大气静稳程度的需求。国内学者在对雾-霾天气气象条件的定量描述上开展了许多指数的研发工作,朱蓉等(2001)基于箱模式理论建立了空气污染潜势指数,并开发了城市大气污染数值预报系统(CAPPS);杨元琴等(2009)选取敏感气象要素:气温、气压、风、相对湿度、稳定度,并引入凝结函数开发了空气质量气象参数(PLAM)指数;廖碧婷等(2012)利用K指数、沙氏指数和L指数构建了垂直交换系数,对空气污染物的垂直输送能力进行了评估,并尝试对灰霾天气和无视程障碍天气进行预报;徐大海等(2016)提出了用A值法确定大气环境容量的方法;张恒德等(2017)根据预报经验和历史气象要素统计,挑选与大气污染有关的气象要素及其阈值,通过权重求和初步构建了静稳天气综合指数(SWI);朱蓉等(2018)根据大气自身所具有的通风稀释和湿清除能力,定义大气自净能力指数,给出基于常规气象观测的计算方法。上述指数从不同角度体现了气象条件对空气污染的作用,但在环境气象业务应用中体现气象条件对大气污染的综合影响还有一定难度。本文结合气象业务部门现有数据环境,以大气污染物质量守恒方程为理论基础,构建物理意义明确的气象因子,并选取与大气污染密切相关的气象要素,基于数据挖掘技术建立大气污染潜势分级预测模型,实现大气污染潜势的客观化、定量化、精细化预报。
1 资料与方法选用2015—2021年秋、冬季(10月1日至翌年3月31日)邢台地面、高空气象资料和空气质量指数资料。地面气象资料包括逐日4个标准时次的资料(气温、气压、风速)及日资料(平均气温、平均气压、相对湿度、平均风速和降水量);高空气象资料为逐日4个标准时次的1 000、925、850、700、600和500 hPa的气温、位势高度、风速。其中地面气象资料及08时、20时(北京时,下同)的高空气象资料由河北省气象信息中心提供;02时的高空资料由前一日20时和当日08时的相应资料计算平均获得,14时的高空资料由当日08时和20时的相应资料计算平均获得。地面及1 000、925和850 hPa的日平均垂直速度,为距离邢台站最近格点(37.5°N、115.0°E) 再分析资料(源自NCEP/NCAR,https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html)。逐日的空气质量指数(AQI)资料来源于河北省生态环境监测中心空气质量实时发布平台。
本研究主要应用统计分析方法中的聚类分析(施能,2009)和Bayes判别分析(Friedman et al,1997)方法。
2 大气背景场的分类杨旭等(2017)对京津冀地区冬半年空气污染天气进行了分型研究,表明不同天气类型下影响污染物扩散、输送、生成和转化的气象条件有所差异。周须文等(2020)对京津冀地区冬半年雾-霾消散大气进行了分类,表明在不同类型大气下,对雾-霾消散的影响因子及其贡献也不相同。因此有必要先对大气背景场进行分类研究。
2.1 大气背景场的聚类分析对流层是大气圈最靠近地面的一层,受太阳辐射与大气环流的影响,对流层中下层的气流运动对天气现象的发生及大气污染物的扩散、输送和转化影响最大。对流层大气的气流运动状态可由各气压层气团热力性质变化来表征,因此选取对流层中下层标准气压层(500、600、700、850、925、1 000 hPa)08时的24 h变温和代表整个气柱冷暖气团变化的地面24 h变压作为研究大气背景场因子。
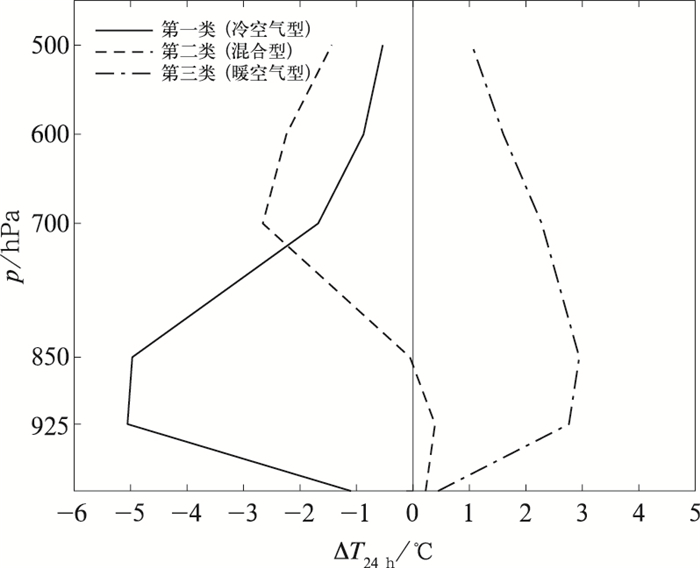
对邢台2017—2019年秋、冬季逐日大气362个个例进行Q型聚类,分析自动生成的不同数量的分类个例特征,认为把大气背景场分三类的个例特征具有明确的天气学意义。图 1是大气分三类中个例24 h变温因子(ΔT24 h)合成,可以清楚看出三类大气特征具有明显差异:第一类对流层中下层(500 hPa以下)均是明显的负变温;第三类均是正变温;第二类在边界层内(850 hPa以下)为正变温,边界层以上(850~500 hPa)为负变温。表明第一类大气对流层中下层冷气团移入为主,称为冷空气型;第二类大气在边界层内以正变温为主,边界层以上以负变温为主,对流层中下层呈上冷下暖的分布特征,称为混合型;第三类大气对流层中下层均为正变温,说明多为暖气团移入,称为暖空气型。这三类清楚地表明了边界层上部自由大气的运动状态。
|
图 1 2017—2019年秋、冬季邢台个例合成的三种大气环流类型的气压-变温图 Fig. 1 Vertical distributions of temperature change and pressure for three atmospheric types in Xingtai during autumn and winter from 2017 to 2019 |
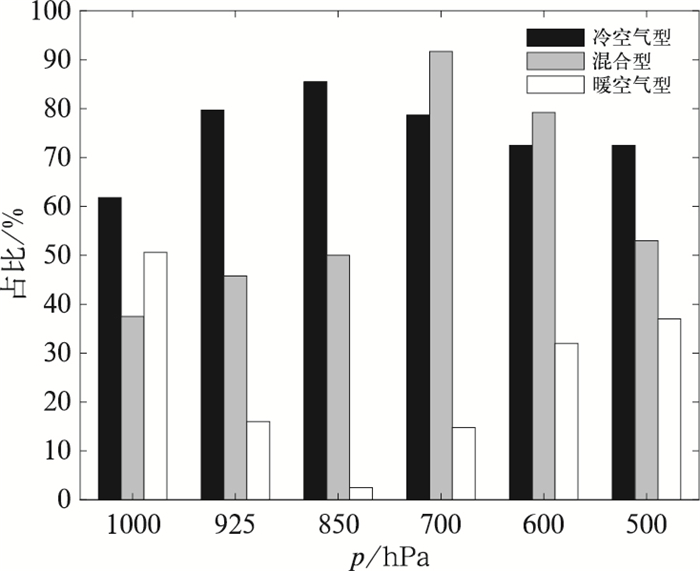
为了比较各气压层24 h变温因子在三类大气中的分布差异,对三类大气中24 h变温≤0的个例数占该类总个例数的百分比进行统计。根据三类大气型的天气学意义,冷空气型大气中,24 h变温≤0的个例数占比越大越好;暖空气型大气中,24 h变温≤0的个例数占比越小越好。由图 2可见,冷空气型大气中850 hPa的24 h变温≤0的个例数占比最大,为81.6%;暖空气型大气中850 hPa的24 h变温≤0的个例数占比最少,只有2.5%;表明850 hPa的24 h变温因子在冷空气型和暖空气型大气中重叠个例最少。混合型大气中850 hPa的24 h变温≤0的个例数占比为50%,说明该因子中位数为0,其值大多在0附近。从各类型大气因子平均值(图 1)看到:在850 hPa层上,混合型大气因子平均值接近0,而冷空气型和暖空气型因子平均值与混合型大气因子平均值相差都较大,显然850 hPa的24 h变温因子较其他气压层的因子对三类大气更具代表性。因此采用850 hPa的24 h变温因子作为大气背景分类的指标气象因子。
|
图 2 2017—2019年秋、冬季邢台三种大气环流类型24 h变温≤0的个例占比 Fig. 2 The case proportions of ΔT24 h≤0 for three atmospheric types in Xingtai during autumn and winter from 2017 to 2019 |
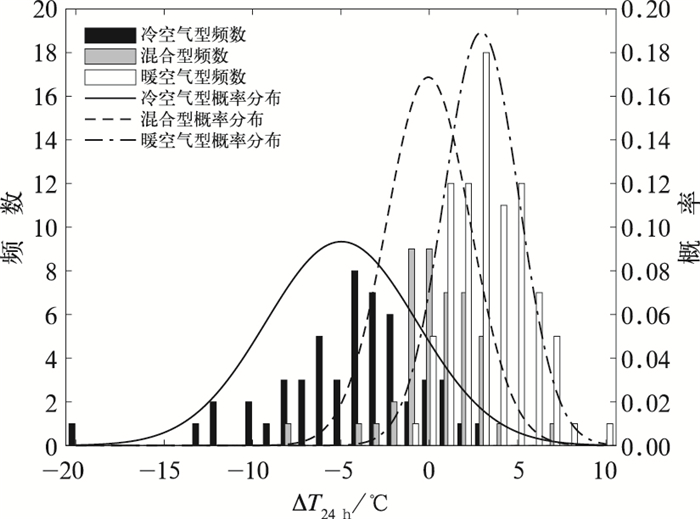
统计850 hPa的24 h变温因子在各类大气中的频数及概率分布(图 3),三类大气环流背景下的24 h变温因子发生频次均呈现单峰形态,并且冷空气型、混合型和暖空气型因子自左至右呈错峰分布,峰值位置具有明显的差异。它们的概率分布都具有正态分布特征,相邻两类之间呈双峰结构,采用双峰法选择阈值,即双峰之间的最低谷处就是两类分割的阈值,根据这一原理可以计算相近两类大气的分割阈值。计算结果显示,冷空气型与混合型大气分割阈值为-2.84℃,混合型与暖空气型大气分割阈值为1.36℃。根据上述阈值对邢台2017—2019年秋、冬季逐日大气进行区分,区分三类大气环流类型的正确百分率分别为:69%(冷空气型)、61%(混合型)、78%(暖空气型)。表明选取的指标因子及其阈值对大气背景具有较好的分类效果。
|
图 3 2017—2019年秋、冬季邢台24 h变温因子在三种大气环流类型中的频数和概率分布 Fig. 3 Frequency and probability distribution of ΔT24 h factor for three atmospheric types in Xingtai during autumn and winter from 2017 to 2019 |
根据大气污染物质量守恒方程(龚强等,1999):
| $ \frac{\partial C}{\partial t}=-v \cdot \nabla_2 C-\omega \frac{\partial C}{\partial p}+\nabla_3\left(K \nabla_3 C\right)+Q+H $ | (1) |
式中: C为大气中的污染物浓度, v为水平风速, ω为垂直速度, p为气压, K为湍流扩散系数, Q为污染物的排放量, H为湿沉降量, ∇2代表水平二维向量算子,∇3代表空间三维向量算子。
从式(1)可见,某地污染浓度变化取决于平流扩散、对流扩散、湍流扩散、污染物排放和湿沉降五大项。假设污染物排放量没有变化,污染浓度变化主要由其余四项决定。大气低层污染物的扩散和清除主要发生在混合层内, 那么大气对污染物的平流扩散能力可用混合层的大气通风量表示:
| $ V_{\mathrm{E}}=\int_0^h u(z) \mathrm{d} z $ | (2) |
式中:VE为大气通风量,u(z)为混合层内z高度的风速,h为混合层高度。
对流扩散是大气垂直运动的结果,因此对流扩散能力由大气边界层内的垂直速度ω来表示。
湍流扩散是大气中不规则、无组织的时空尺度跨度很大的气团运动,分为机械湍流和热力湍流。机械湍流激发的扩散能力可用风速的垂直切变率来表示:
| $ V_{\mathrm{R}}=\frac{u_2-u_1}{z_2-z_1} $ | (3) |
式中:VR表示风速的垂直切变率,z2、z1表示两个气压层的高度,u2、u1表示两个气压层的风速。
热力湍流主要是在垂直方向产生温度梯度而造成的。国际原子能机构在1980年推出了温度梯度法,即用两层大气间铅直方向的温度梯度来表示垂直方向上的湍流状态,判据可表示为:
| $ T_{\mathrm{R}}=\frac{\Delta T}{\Delta z} $ | (4) |
式中:TR表示铅直方向温度梯度,ΔT表示两个气压层的温度差,Δz表示两个气压层的厚度。
湿沉降是指降水对大气中污染物冲刷使得大气中污染物浓度降低。湿沉降能力(Vw)可表示为:
| $ V_{\mathrm{w}}=W_{\mathrm{r}} r $ | (5) |
式中:Wr表示雨洗常数,取6×105; r为降水率。
3.2 气象因子的计算方法(1) 混合层高度
大气边界层的上限高度即为混合层高度,因天气条件而异,白天与夜晚不同,城乡也有明显差别。在中纬度城市,通常晴天的白天混合层高度可达到1000~1500 m(850 hPa),夜晚只有200 m左右。由于受观测资料所限,把850 hPa以下的大气认为是大气边界层,由于大气边界层内不同高度的气象因子对污染物迁移扩散作用不同,根据气象部门现有的气象资料,把混合层高度按标准气压层(850 hPa、925 hPa)分为两段(地面至925 hPa、925~850 hPa)分别进行计算。
根据天气学原理, 两等压面之间的厚度计算公式为:
| $ h=R T_{\mathrm{m}} \ln \left(\frac{p_1}{p_0}\right) / 9.8 $ | (6) |
式中:比气体常数R=2.87,Tm=0.5(T1+T0)(等压面p1和p0的气温平均值); 地面至925 hPa的厚度记为h1,925~850 hPa的厚度记为h2; 混合层高度:h=h1+h2。
(2) 平流扩散因子——大气通风量
地面至925 hPa的通风量:VE1=0.5(u地面+u925)h1
925~850 hPa的通风量:VE2=0.5(u925+u850)× h2
(3) 对流扩散因子——垂直速度
选取了地面(ω地)和边界层内标准气压层的垂直速度(ω1000, ω925, ω850)。
(4) 机械湍流因子——风速垂直切变
地面至925 hPa的风切变:VR1=(u925-u地面)/h1
925~850 hPa的风切变:VR2=(u850-u925)/h2
(5) 热力湍流因子——垂直温度梯度
地面至925 hPa的温度梯度:TR1=(T925-T地面)/h1
925~850 hPa的温度梯度:TR2=(T850-T925)/h2
(6) 湿沉降因子
湿沉降因子代表的是降水对大气中污染物的冲刷能力,因此选取24 h降水量作为湿沉降因子。
3.3 大气污染潜势气象因子的选取根据实际气象资料情况,选取地面和边界层内标准气压层的日平均垂直速度作为对流扩散因子;选取24 h降水量作为湿沉降因子,因子对应符号见表 1。平流扩散因子选取大气边界层内2个高度层4个时次的大气通风量,共8个因子;湍流扩散因子选取大气边界层内2个高度层4个时次的风速垂直切变、垂直温度梯度,共16个因子。因子对应符号见表 2。另外,根据杨元琴等(2009)、张恒德等(2017)的研究成果,选取了地面敏感气象要素:日平均气温、日平均气压、日平均相对湿度、日平均风速、24 h变压、24 h变温,因子对应符号见表 3。
|
|
表 1 对流扩散因子、湿沉降因子的名称、符号对照 Table 1 Reference table of atmospheric factor symbols for convection diffusion and wet depositions |
|
|
表 2 平流扩散因子、湍流扩散因子的名称、符号对照 Table 2 Reference table of atmospheric factor symbols for advection and turbulent diffusion |
|
|
表 3 地面气象因子的名称、符号对照 Table 3 Reference table of atmospheric factor symbols for factor symbols in surface |
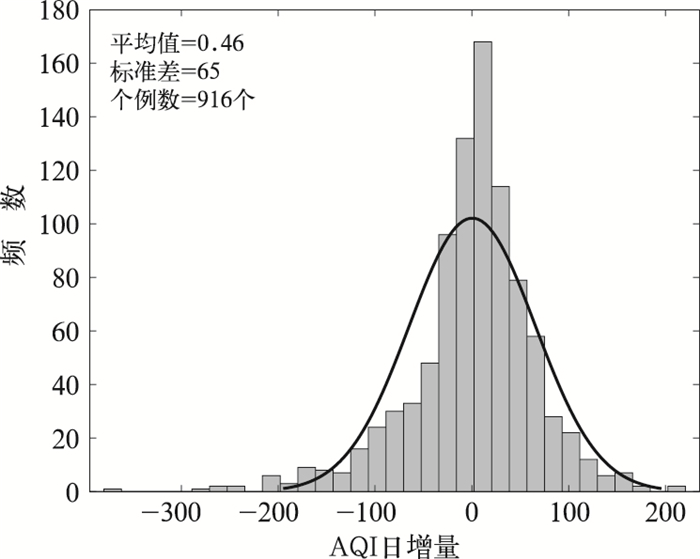
大气污染潜势直接影响空气质量的变化,因此大气污染潜势的分级可依据AQI日增量来划分。对2015—2019年秋、冬季邢台AQI日增量统计分析(图 4):AQI日增量出现频率呈正态分布,AQI日增量平均值为0.46,标准差为65,表明大气污染潜势五级划分比较合理;参考全国气象防灾减灾标准化技术委员会(2018),把AQI日增量-80、-30、30、80作为分界值(表 4)。划分的AQI日增量五分级与AQI日增量的相关性为0.95,说明AQI日增量五分级能较好代表AQI日变化状况。
|
图 4 2015—2019年秋、冬季邢台AQI日增量分布 Fig. 4 Frequency distribution of AQI daily increment in Xingtai during autumn and winter from 2015 to 2019 |
|
|
表 4 污染潜势五级等级标准和描述 Table 4 Five grades of air pollution potential |
创建预测模型采用的是2017—2019年秋、冬季邢台的资料。首先对建模资料进行处理:(1)根据大气背景分类指标因子及其阈值对研究的个例进行识别分类,建立冷空气型、混合型和暖空气型三类大气影响因子数据库。(2)对各类型大气个例的AQI日增量按表 4的污染潜势五分级标准进行划分,构建带有标号的模型创建训练数据集。
由于选取的变量因子较多,在应用Bayes判别方法建立判别函数过程中,通过逐步选择法对自变量因子进行筛选,剔出了最低容差水平在0.001以下的变量,最后保留了对模型判别贡献较大的变量因子。通过对数据集训练确定了五分级判别函数的变量因子系数(表 5~表 7)。对比表 5~表 7发现,不同大气背景的五分级判别函数,参与的变量因子及其权重都有所不同,说明大气中污染物的聚集和消散是复杂多变的,不同大气背景下其变化机制存在较大差异,分类建立预测模型是必要的。
|
|
表 5 冷空气型大气污染潜势五分级判别函数系数 Table 5 Five grades discriminant function of pollution potential for cold air type |
把大气污染潜势1~5级判别函数的预测概率依次记为:P1、P2、P3、P4、P5,以冷空气型为例,给出了大气污染潜势五分级预测模型:
P1=-64.292+1.57X1-0.611X2+0.547X3+5.886X4+0.064X5+0.027X6-0.085X7-0.055X9-0.031X10+0.09X11+11.545X12+24.352X13-48.602X14-9.236X15-11.778X16-18.647X17+113.96X18+74.001X19-211.39X20+ 169.279X22+47.454X23-184.127X24-64.508X25+292.146X26-276.66X27+79.364X28
P2=-59.405+1.44X1-0.75X2+0.56X3+6.435X4+0.057X5+0.019X6-0.076X7-0.05X9-0.02X10+0.08X11+11.322X12+26.816X13-50.867X14-10.223X15-8.168X16-20.104X17+102.322X18+57.35X19-190.612X20+154.69X22+32.032X23-163.631X24-52.518X25+260.469X26-231.071X27+58.711X28
P3=-51.758+1.232X1-0.475X2+0.533X3+5.618X4+0.045X5+0.02X6-0.064X7-0.039X9-0.023X10+0.068X11+4.901X12+29.293X13-44.598X14-12.488X15-5.91X16-15.585X17+80.267X18+53.149X19-157.361X20+125.881X22+33.865X23-137.354X24-57.87X25+230.189X26-164.605X27+27.415X28
P4=-64.256+1.587X1-0.225X2+0.58X3+5.475X4+0.064X5+0.03X6-0.09X7-0.055X9-0.03X10+0.095X11+8.999X12+31.485X13-51.804X14-10.711X15-4.901X16-18.594X17+106.541X18+76.41X19-224.287X20+176.865X22+40.092X23-195.532X24-72.354X25+249.041X26-170.643X27+36.046X28
P5=-65.768+2.219X1+1.136X2+0.391X3+3.353X4+0.078X5-0.099X7-0.067X9-0.007X10+0.101X11+39.136X12+10.229X13-63.095X14-19.838X15-24.892X16+3.473X17+122.395X18+28.08X19-239.453X20+ 188.553X22-10.007X23-210.011X24+7.676X25+246.443X26-277.51X27+85.526X28
上述判别函数通过自身验证得到的大气污染潜势五级判别正确率为75.2%,其中冷空气型预测模型判别正确率为80.0%,混合型为71.0%,暖空气型为74.7%。
5 大气污染潜势五分级预测模型检验 5.1 模型独立检验模型独立检验法是对判别分析得到的判别函数效果评判最客观有效的方法。把2015—2016年秋、冬季邢台逐日气象资料代入预测模型中,比较各级判别函数值(P1, P2, P3, P4, P5)的大小,根据Bayes判别准则,函数值最大代表所对应级别出现概率最大,即是预测级别。把污染潜势预测级别与实际AQI日增量级别进行对比,预测级别与AQI日增量级别相一致的记为正确,预测正确日数占实际出现日数的百分比即为预测正确率。表 8为2015—2016年秋、冬季邢台污染潜势五分级预测正确率,看到三类大气的预测模型虽然对各等级的污染潜势预测正确率存在差别,但对各等级正确率的分布形态基本一致。都对大气处于正常状态的三级预测最好,正确率在80%以上;其次是非常利于大气污染物扩散的一级和非常不利于扩散的五级,它们的各级正确率分别为64.8%和59.1%。该预测模型对2015—2016年秋、冬季邢台污染潜势五分级预测综合正确率为63.6%,能较好预测大气对污染物的聚集、扩散能力。
|
|
表 8 2015—2016年秋、冬季邢台污染潜势五分级预测正确率(单位:%) Table 8 Five grades prediction accuracy of air pollution potential during autumn and winter from 2015 to 2016 (unit: %) |
大气自净能力指数(ASI)是对雾-霾天气气象条件定量描述指数,它反映的是大气运动对污染物的通风稀释作用和降水对污染物的湿清除作用。根据朱蓉等(2018)提出的ASI计算方法,计算邢台2019—2021年秋、冬季的ASI。
为了便于与预测模型判别结果对比,同样将ASI划分为五级进行评价。ASI五级划分依据具体为:(1)ASI按2.5 t·d-1·km-2和4.1 t·d-1·km-2两个限值,分为优、良和一般三个评价等级(全国气候与气候变化标准化技术委员会, 2020)。(2)根据朱蓉等(2018)对ASI的研究,当ASI低于1.4 t·d-1·km-2时,京津冀地区容易出现AQI达到200的空气质量重污染等级;(3)结合ASI与AQI日增量的统计分析,当ASI低于0.4 t·d-1·km-2时,AQI日增量在80以上,ASI的分级阈值和等级描述见表 9。ASI划分的五分级与ASI的相关系数为-0.915(表 10),通过了α=0.01显著性水平检验,表明该五分级能较好地代表大气的自净能力指数。
|
|
表 9 ASI评价等级 Table 9 Evaluation grads of ASI |
对2019—2021年秋、冬季邢台逐日AQI日增量、ASI和污染潜势五分级等预测进行了双变量相关分析(表 10),可以看到:AQI日增量五分级与AQI日增量相关系数为0.947,表明AQI日增量五分级能较好地代表大气对物的稀释扩散能力。ASI五分级与AQI日增量、AQI日增量五分级的相关性均高于ASI,说明ASI五分级在对大气扩散能力的描述上优于ASI;污染潜势五分级预测与AQI日增量、AQI日增量五分级的相关性分别为0.676和0.679,明显高于ASI和ASI五分级。显然污染潜势五分级模型预测结果优于ASI。
|
|
表 10 2019—2021年秋、冬季邢台不同预测结果的相关性分析 Table 10 The correlation coefficients in different forecasts in Xingtai during autumn and winter from 2019 to 2021 |
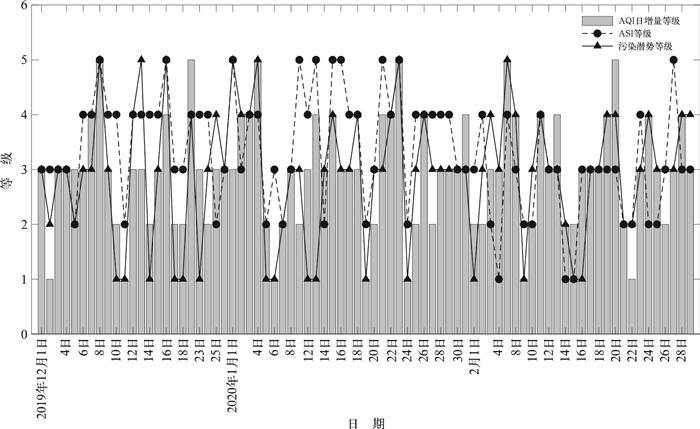
图 5为2019年12月1日至2020年2月29日邢台逐日AQI日增量等级实况和ASI等级、污染潜势等级预测结果,无论是正常生产时段还是疫情封闭时段(2020年1月24日至2月29日),AQI日增量等级变化没有明显差异,说明AQI日增量主要受大气条件的影响,污染物排放量对其影响不大;模型判别的污染潜势等级与AQI日增量等级的变化趋势具有较高的一致性,明显好于ASI等级;模型对极利于扩散的一级和极不利于扩散的五级判别正确次数明显高于ASI;模型判别的污染潜势等级与AQI日增量等级实况基本上是相同或相差一级,而ASI等级与AQI日增量等级相差两级以上的较多。显然,模型对大气污染潜势的五级判别能力好于ASI。
|
图 5 2019年12月1日至2020年2月29日邢台AQI日增量、ASI、污染潜势预测的等级时间序列 Fig. 5 Time series of AQI daily increment, ASI and model prediction grads in Xingtai from 1 December 2019 to 29 February 2020 |
介绍了应用数据挖掘技术研究大气污染潜势分级预报方法,对邢台建立的大气污染潜势五分级预测模型进行了检验分析,得到结论如下:
(1) 通过对大气环流背景的分类研究,发现大气背景场可分为具有明确物理意义的三种大气环流类型(冷空气型、混合型、暖空气型),850 hPa的24 h变温是区分三类大气环流的最佳指标因子;采用双峰法选择的指标因子阈值能较好地区分三类大气环流,对冷空气型、混合型、暖空气型大气区分正确率分别为69%、61%和78%。
(2) 应用数据挖掘技术客观选取变量因子及其权重,结果表明:大气中污染物的聚集和消散都是复杂的过程,有众多因子参与,不同大气背景各因子的贡献有较大差异。
(3) 建立的大气污染潜势五分级预测模型能较好地对AQI日增量进行五级判别,综合判别正确率为63.6%,其中冷空气型预测模型综合判别正确率最高,为70.6%。
(4) 大气污染潜势五分级预测模型的判别结果与实际大气AQI日增量等级的变化趋势具有较高的一致性,相关系数在0.67以上;明显好于ASI对污染潜势五分级的预测结果。
数据挖掘大多数是大而全、多而精,数据越多模型越可能精确,变量越多,数据之间的关系越明确。由于受到现有气象资料的限制,对气象因子的选用和计算都较粗,随着观测技术的进步,还需要在选取因子及其计算方面不断改进,使建立的预测模型准确率不断提高。
蔡子颖, 姚青, 韩素芹, 等, 2017. 21世纪以来天津细颗粒物气象扩散能力趋势分析[J]. 中国环境科学, 37(6): 2040-2046. Cai Z Y, Yao Q, Han S Q, et al, 2017. The trends of fine particulate meteorological diffusivity in Tianjin form 21th[J]. China Environ Sci, 37(6): 2040-2046 (in Chinese). DOI:10.3969/j.issn.1000-6923.2017.06.006
|
龚强, 白乐生, 杨宏斌, 1999. 空气污染潜势指数预报方法[J]. 气象与环境学报, 15(3): 46-47. Gong Q, Bai L S, Yang H B, 1999. Prediction method of air pollution potential index[J]. J Meteor Environ, 15(3): 46-47 (in Chinese).
|
江琪, 王飞, 张恒德, 等, 2017. 北京市PM2.5和反应性气体浓度的变化特征及其与气象条件的关系[J]. 中国环境科学, 37(3): 829-837. Jiang Q, Wang F, Zhang H D, et al, 2017. Analysis of temporal variation characteristics and meteorological conditions of reactive gas and PM2.5 in Beijing[J]. China Environ Sci, 37(3): 829-837 (in Chinese).
|
廖碧婷, 吴兑, 陈静, 等, 2012. 灰霾天气变化特征及垂直交换系数的预报应用[J]. 热带气象学报, 28(3): 417-424. Liao B T, Wu D, Chen J, et al, 2012. A study of the variation trends of haze and application of the vertical exchange coefficient[J]. J Trop Meteor, 28(3): 417-424 (in Chinese). DOI:10.3969/j.issn.1004-4965.2012.03.014
|
梅梅, 朱蓉, 孙朝阳, 2019. 京津冀及周边"2+26"城市秋冬季大气重污染气象条件及其气候特征研究[J]. 气候变化研究进展, 15(3): 270-281. Mei M, Zhu R, Sun C Y, 2019. Study on meteorological conditions for heavy air pollution and its climatic characteristics in "2+26" cities around Beijing-Tianjin-Hebei Region in autumn and winter[J]. Climate Change Res, 15(3): 270-281 (in Chinese).
|
全国气候与气候变化标准化技术委员会, 2020. 气候资源评价气候宜居城镇: QX/T 570-2020[S]. 北京: 气象出版社. Committee 540 on Climate and Climate Change of Standardization Administration of China, 2020. Climate resource assessment-Climate livable cities: QX/T 570-2020[S]. Beijing: China Meteorological Press(in Chinese).
|
全国气象防灾减灾标准化技术委员会, 2018. 空气污染扩散气象条件等级: QX/T 413-2018[S]. 北京: 气象出版社. Committee 345 on meteorological disaster prevention and mitigation of Standardization Administration of China, 2018. Grades of air pollution diffusion meteorological conditions: QX/T 413-2018[S]. Beijing: China Meteorological Press(in Chinese).
|
尚可, 杨晓亮, 张叶, 等, 2016. 河北省边界层气象要素与PM2.5关系的统计特征[J]. 环境科学研究, 29(3): 323-333. Shang K, Yang X L, Zhang Y, et al, 2016. Statistical analysis of the relationship between meteorological factors and PM2.5 in the boundary layer over Hebei Province[J]. Res Environ Sci, 29(3): 323-333 (in Chinese).
|
施能, 2009. 气象统计预报[M]. 北京: 气象出版社: 206-219. Shi N, 2009. Meteorological Statistical Forecast[M].
Beijing: China Meteorological Press: 206-219 (in Chinese).
|
徐大海, 王郁, 朱蓉, 2016. 大气环境容量系数A值频率曲线拟合及其应用[J]. 中国环境科学, 36(10): 2913-2922. Xu D H, Wang Y, Zhu R, 2016. The atmospheric environmental capacity coefficient cumulative frequency curve fitting and its application[J]. China Environ Sci, 36(10): 2913-2922 (in Chinese). DOI:10.3969/j.issn.1000-6923.2016.10.006
|
杨旭, 张小玲, 康延臻, 等, 2017. 京津冀地区冬半年空气污染天气分型研究[J]. 中国环境科学, 37(9): 3201-3209. Yang X, Zhang X L, Kang Y Z, et al, 2017. Circulation weather type classification for air pollution over the Beijing-Tianjin-Hebei Region during winter[J]. China Environ Sci, 37(9): 3201-3209 (in Chinese). DOI:10.3969/j.issn.1000-6923.2017.09.001
|
杨元琴, 王继志, 侯青, 等, 2009. 北京夏季空气质量的气象指数预报[J]. 应用气象学报, 20(6): 649-655. Yang Y Q, Wang J Z, Hou Q, et al, 2009. A PLAM index forecast method for air quality of Beijing in summer[J]. J Appl Meteor Sci, 20(6): 649-655 (in Chinese). DOI:10.3969/j.issn.1001-7313.2009.06.001
|
于文金, 吴雁, 黄亦露, 等, 2016. 河北省雾霾波动变化特征及成因研究[J]. 大气科学学报, 39(4): 554-561. Yu W J, Wu Y, Huang Y L, et al, 2016. The variation and genesis of haze in Hebei Province[J]. Trans Atmos Sci, 39(4): 554-561 (in Chinese).
|
张恒德, 张碧辉, 吕梦瑶, 等, 2017. 北京地区静稳天气综合指数的初步构建及其在环境气象中的应用[J]. 气象, 43(8): 998-1004. Zhang H D, Zhang B H, Lyu M Y, et al, 2017. Development and application of stable weather index of Beijing in environmental meteorology[J]. Meteor Mon, 43(8): 998-1004 (in Chinese).
|
周须文, 韩世茹, 井元元, 等, 2020. 京津冀雾霾消散因子及其阈值研究[J]. 气象学报, 78(1): 154-162. Zhou X W, Han S R, Jing Y Y, et al, 2020. A study on haze dissipation factors and their thresholds over Beijing-Tianjin-Hebei Area[J]. Acta Meteor Sin, 78(1): 154-162 (in Chinese).
|
朱蓉, 徐大海, 孟燕君, 等, 2001. 城市空气污染数值预报系统CAPPS及其应用[J]. 应用气象学报, 12(3): 267-278. Zhu R, Xu D H, Meng Y J, et al, 2001. City air pollution numerical prediction system and its application[J]. Quart J Appl Meteor, 12(3): 267-278 (in Chinese). DOI:10.3969/j.issn.1001-7313.2001.03.002
|
朱蓉, 张存杰, 梅梅, 2018. 大气自净能力指数的气候特征与应用研究[J]. 中国环境科学, 38(10): 3601-3610. Zhu R, Zhang C J, Mei M, 2018. The climate characteristics of atmospheric self-cleaning ability index and its application in China[J]. China Environ Sci, 38(10): 3601-3610 (in Chinese). DOI:10.3969/j.issn.1000-6923.2018.10.001
|
Ding Y H, Liu Y J, 2014. Analysis of long-term variations of fog and haze in China in recent 50 years and their relations with atmospheric humidity[J]. Sci China Earth Sci, 57(1): 36-46. DOI:10.1007/s11430-013-4792-1
|
Friedman N, Geiger D, Goldszmidt M, 1997. Bayesian network classifier[J]. Mach Learn, 29(1): 131-163.
|
Tai A P K, Mickley L J, Jacob D J, 2010. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: implications for the sensitivity of PM2.5 to climate change[J]. Atmos Environ, 44(32): 3976-3984. DOI:10.1016/j.atmosenv.2010.06.060
|
Wang J X L, Angell J K, 1999. Air stagnation climatology for the United States (1948-1998)[R]. Silver Spring, MD: National Oceanic and Atmospheric Administration.
|
 2022, Vol. 48
2022, Vol. 48 