2. 中国民用航空中南地区空中交通管理局气象中心,广州 510405
2. Meteorological Center of Central South Air Traffic Management Bureau of CAAC, Guangzhou 510405
基于雷达回波进行外推预报是对流临近预报的最基础方法,特别是预报时效在0~2 h的临近预报,雷达回波外推方法依然在目前业务系统中占据主导地位。关于雷暴的临近预报,Wilson et al(1998)做了非常详细的综述,郑永光等(2010)、俞小鼎和郑永光(2020)对于强对流的临近预报技术也做了比较完整的介绍。
基于雷达回波外推基本可以分为两大类方法:一是雷暴单体质心的识别与跟踪技术,主要基于2D或者3D反射率资料来识别、跟踪、预报雷暴的质心位置,进行对流系统的外推预报。典型方法包括WSR-88D风暴序列算法(Fulton et al, 1998)、SCIT(the storm cell identification and tracking; Johnson et al, 1998)、TITAN(the thunderstorm identification, tracking, analysis and nowcasting;Dixon and Wiener, 1993;Han et al,2009)。二是追踪雷达回波图像的运动,例如光流法和TREC方法(tracking radar echoes by correlation)。光流法(Horn and Schunck, 1981;Lucas and Kanade, 1981;Bowler et al,2004;曹春燕等,2015)通过计算雷达回波的光流场得到回波的运动矢量场,从而基于光流运动矢量场对雷暴回波进行外推临近预报。TREC方法(Rinehart and Garvey, 1978;曾小团等,2010)假定空间散射粒子完全由风力驱动,通过对两个连续时次体扫描的雷达回波进行相关分析,估计出运动矢量场。TREC方法不依赖对流系统质心的识别,在许多对流临近预报系统中得到了广泛应用,并且得到了极大发展。
TREC改进方法主要包括:COTREC(the continuity of TREC)和基于交叉相关的多尺度雷达回波跟踪方法(the multi-scale tracking radar echoes by correlation, MTREC)。考虑到地形遮挡、回波变化快等原因,TREC分析的速度经常存在不连续,Li et al(1995)提出了COTREC,以二维连续性方程作为强约束条件,利用观测距离和计算位移构造价值函数,通过变分技术平滑速度场,既改进了与地形相关的降水的临近预报效果,也一定程度上改进了强风暴的外推预报效果。COTREC方法的基本原理是对传统交叉相关法(TREC)反演的风场进行水平无辐散处理,得到COTREC风场,用新的风场外推得出的回波能够保持平滑连续的形状。但是这种方法也存在缺陷,由于采用水平无辐散限制,使得外推反演得到的风场在不同程度上受到削弱,从而导致外推的回波略慢于实况观测的回波(陈雷等,2009)。Wang et al(2013)基于MTREC方法,分析不同尺度的回波移动矢量场,将大尺度的系统性移动矢量场和小尺度的内部移动矢量场进行合成,综合得到外推运动场。虽然MTREC方法提出了将雷达回波外推运动场由大尺度的系统性运动和小尺度的内部移动进行合成,具有理论上合理性,但是其大尺度和小尺度的划分依然是根据经验决定的,无法根据实际天气系统的尺度来进行选取“跟踪区域”的大小。
目前所有的TREC类跟踪方法通常都是将整体的回波划分为固定大小的跟踪区域,通过在相邻时次回波图中搜索相关系数最大的区域来确定回波的移动。实际上,王改利和刘黎平(2007)指出TREC类方法将整幅雷达图像分成若干个固定矩形网格,本身对云团的划分物理意义就不够明确。在实际应用当中,TREC类方法采用的分析跟踪区域大小都是根据平均统计或者人为经验来划分的,但是通常不同尺度的回波移动方向总是不一致(Houze et al, 1993)。当TREC类方法将雷达回波场划分的跟踪区域太小时,部分系统性的移动信息会被忽略,而当TREC类方法跟踪区域取得太大时,反演的运动场又过于平直,且往往造成小尺度的雷暴系统会由于跟踪单元内样本数量不够而被忽略(Tuttle and Foote, 1990)。所以本文提出了一种自适应尺度的雷达回波交叉相关跟踪方法(the adaptive-scale tracking radar echoes by correlation,ATREC),其可根据实际雷达回波的大小,确定跟踪区域的特征尺度,再通过自我分裂在特征区域内部划分为更小的次级尺度进行多尺度跟踪,最后得到多尺度合成的运动场作为雷达回波外推运动场,进行临近外推预报。本文通过不同尺度和不同类型的实际个例,对比MTREC方法或TREC方法,验证ATREC方法的可行性,并评估预报效果。通过2016年4月总共128个例,进行综合统计检验评估,论证ATREC方法在实际业务中可行性和有效性。
1 数据和质量控制本文所使用的雷达资料来自广州市气象局的S波段雷达,采样扫描频率为6 min,体扫模式为VCP21,包含9个仰角(仰角由低到高, 即为0.5°,1.5°,2.4°,3.4°,4.3°,6.0°,9.9°,14.6°,19.5°)。个例分析采用的降水过程来自2013年4月30日的飑线个例,2016年5月20日的大范围混合降水过程,2016年5月9日的多单体雷暴个例和2016年6月26日的对流单体雷暴个例。综合统计分析采用2016年4月总共30天的个例资料。
雷达反射率资料预处理和质量控制主要有:(1)去除地物回波,(2)中值滤波,(3)去除距离折叠,(4)线性插值将雷达坐标系数据插值到直角坐标系。雷达回波矢量追踪中, 需要选取特定高度上回波作为最具代表性的一层雷达回波场,本文采用3 km高度的反射率作为对流系统的表征,考虑仰角的影响,通常3 km数据在230 km半径范围内有效,所以本文分析的天气个例发生在雷达中心230 km以内。
2 方法和方案设计 2.1 TREC方法TREC方法的基本原理是将反射率图像划分为一系列固定大小的矩阵,通过计算连续时次雷达回波在不同区域的空间相关,搜索与目标区域具有最优相关系数的区域,从而得到回波的运动矢量场。主要步骤如下:
(1) 将雷达回波反射率资料进行插值网格化后,选取对流系统最具有代表性的某一层回波,将该层二维反射率场划分为若干大小相等的区域,通常采用正方形,每个区域具有相同的资料格点数。
(2) 将t0时刻每个区域作为目标区域,分别与下一个时次t1时刻搜索半径内的所有区域做空间交叉相关计算。其相关系数可以表示为:
| $ R(m, n)=\frac{\sum\limits_{i} \sum\limits_{j}[Z(i+n, j+m, t+\Delta t)-\bar{Z}(t+\Delta t)][Z(i, j, t)-\bar{Z}(t)]}{\sqrt{\sum\limits_{i} \sum\limits_{j}[Z(i+n, j+m, t+\Delta t)-\bar{Z}(t+\Delta t)]^{2} \sum\limits_{i} \sum\limits_{j}[Z(i, j, t)-\bar{Z}(t)]^{2}}} $ | (1) |
式中:Z(i,j,t)表示t0时刻,横坐标为i,纵坐标为j的反射率值;m表示从t0到t1间隔x轴方向移动的格点数,n表示从t0到t1间隔y轴方向移动的格点数。通过在搜索半径内改变m, n的值,求得最大相关系数Rmax对应的位置,作为目标回波在t0到t1间隔内所移动的位置,从而得到移动矢量。
TREC方法将反射率图像划分为一系列固定大小的矩阵,矩阵内的回波采用一致的运动矢量。采用固定大小的追踪单元,对应的相关计算方法比较简单,也便于外推计算,但是存在如何选取追踪单元大小的问题。跟踪单元不能取得太大,这样得到运动信息过于平均,也不能取得太小,这样易于被小尺度的信息干扰,且得到外推矢量场不够平滑。所以通常TREC方法的效果与跟踪单元的大小密切相关。本文将主要参考陈明轩等(2007)对于TREC方法参数的分析和统计,并结合当地经验,将TREC方法参数设置如下:跟踪区域大小取25 km×25 km,跟踪区域间隔取10 km,此外,为有效降低噪声等低阈值回波对TREC算法的影响,通常需要设定最低阈值,本文最低阈值采用15 dBz,同时,每个跟踪“区域”中有效的数据格点数占跟踪“区域”内总格点数的百分率低于一定阈值时,则该“区域”将不进行TREC方法计算,本文将有效数据格点占百分率的阈值设置为60%。
2.2 MTREC方法MTREC方法是在TREC方法的基础上,先采用跟踪区域相对较大的TREC方法来获得大尺度的移动信息,作为雷暴系统性移动的表征,然后再采用区域相对较小的TREC方法来估计小尺度的雷暴内部的运动信息。
主要步骤分为四步:(1)采用跟踪区域较大的TREC方法得到t0时刻到t1时刻的空间分辨率较低的系统性运动矢量场;(2)通过已知的系统性运动矢量场,将t0时刻的雷达回波外推到t1时刻,得到t1时刻预报场;(3)通过对比t1时刻的预报场和观测场,采用跟踪区域尺度较小的TREC方法再次进行交叉相关计算,得到高分辨率的雷暴内部移动信息; (4)将第一步得到系统性运动矢量场和第三步得到雷暴内部运动矢量场进行合成,从而得到用于外推预报的运动矢量场。
MTREC方法将回波运动分为大尺度和小尺度两种不同尺度的移动信息,对应取不同大小的跟踪区域。例如Wang et al(2013)选取的台风和飑线个例,大尺度的跟踪区域取150 km×150 km,小尺度的跟踪区域取20 km×20 km,这样尺度对于台风或者飑线是合适的,但是对于本身只有十几千米,甚至几千米的对流系统,显然是难以得到对应大尺度的系统性移动信息和小尺度的雷暴内部移动信息的。此外,当雷达回波尺度比较小,跟踪区域内的有效数据格点数百分比低于预设阈值时,将不进行TREC方法跟踪计算,会导致小尺度的对流系统被忽略,从而丢失对应移动信息。所以,预设固定大小的跟踪单元会存在一定的弊端。本文使用的数据是基于单多普勒雷达探测,3 km反射率有效探测距离约为230 km,所以本文采用MTREC的大尺度跟踪区域的大小为50 km×50 km,跟踪区域间隔为25 km,小尺度的跟踪区域取25 km×25 km,跟踪区域间隔为10 km。
2.3 ATREC方法ATREC方法通过回波边界识别,得到与对流回波范围相对应的特征尺度区域,然后通过TREC方法得到整块回波的运动速度作为特征尺度运动速度。在特征尺度区域的基础上,将原有的跟踪区域不断划分为次一级的跟踪区域,再通过多尺度TREC方法得到不同尺度的移动矢量场,次级尺度的运动场在上一级尺度的运动场基础上不断迭代细化,最后得到多尺度合成的临近外推运动矢量场。
本研究采用摩尔邻域跟踪算法(Gonzalez et al,2004)来确定回波的区域,其基本原理是:将反射率场转化为像素网格场,低于反射率最低阈值的格点视为白色像素,高于反射率最低阈值的像素视为黑色像素;从网格的左下角开始,从左向右,自下而上扫描每一列像素,直到遇到第一个黑色像素,将其作为起始像素点;之后每次遇到黑色像素,将其设置为当前边界像素点;然后原路返回到先前到达的白色像素,以顺时针方向搜索的摩尔邻域内的每一个像素,直到遇到下一个黑色像素;重复这个过程,当起始像素点被第二次访问时算法终止,在整个运行过程走过的黑色像素就是目标的边界。
引入摩尔邻域跟踪算法实现回波区域的自动识别后,将识别的回波区域作为特征尺度区域,在特征尺度区域的基础上将原有回波区域划分尺度较小的次一级跟踪区域。本文采用等比例自我分裂方式对特征尺度区域进行划分,即根据实际需求,将原特征尺度区域依次划分为2×2, 3×3, 4×4个,以此类推,直至N×N个次级尺度的小区域,从而建立ATREC方法,具体主要步骤分为四步:
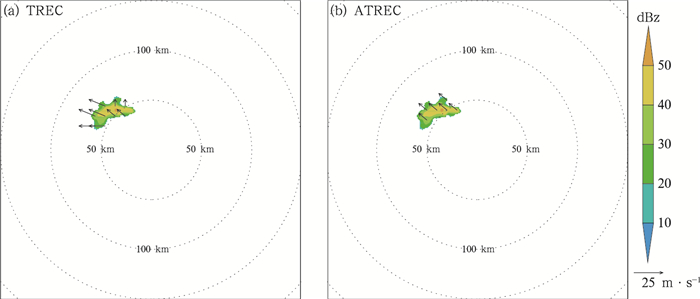
(1) 采用摩尔边界法来获得每一块回波的边界,确定对应特征跟踪单元的大小。按照TREC算法在下一时次回波中搜索对应最相似的区域,得到整块区域回波的运动速度场u0,v0和对应的相关系数R。本文以2013年4月30日的飑线过程为例,边界阈值取15 dBz时,得到边界识别初步的结果如图 1a,其中蓝色框区域为包含目标回波的特征尺度区域。采用特征尺度区域作为跟踪单元,通过TREC算法,在下一时次雷达回波图 1b中求与特征尺度区域同样大小且相关系数最大的区域,得到对应的移动矢量作为特征移动矢量,并作为特征尺度区域内回波的整体移动矢量场,如图 1c。
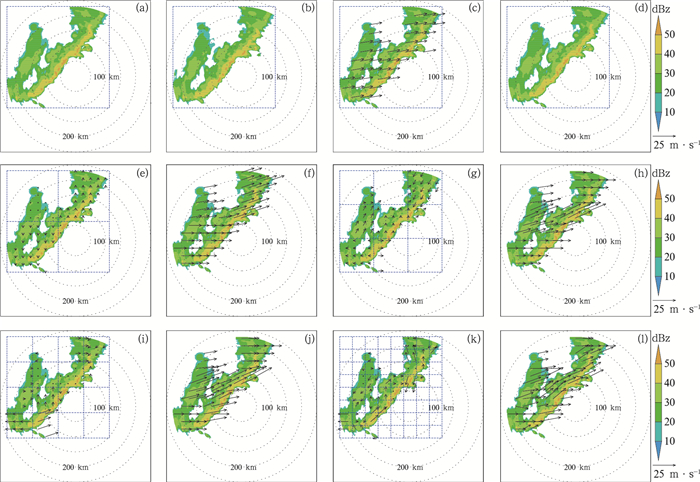
|
图 1 2013年4月30日(a)03:54 UTC雷达回波初始场,(b)04:00 UTC雷达回波实况场,(c)由初始场通过特征尺度运动场或者合成运动场外推预报6 min的雷达回波预报场叠加特征尺度运动场(矢量),(d)特征尺度预报场(阴影),(e)特征尺度预报场(阴影)叠加2×2个单元,3×3个单元次级运动场(矢量),(g)2×2个单元预报场(阴影)叠加3×3个单元次级运动场(矢量),(i)3×3个单元预报场(阴影)叠加4×4个单元次级运动场(矢量),(k)4×4个单元预报场(阴影)叠加8×8个单元次级运动场(矢量);(f, h, j, l)初始场(阴影)分别叠加(f)2×2,(h)3×3,(j)4×4和(l)8×8单元合成运动场(矢量) Fig. 1 (a) Initial field of radar reflectivity at 03:54 UTC; (b) observed field of radar reflectivity at 04:00 UTC 30 April 2013; (c) forecasting field with radar reflectivity based on the 6 min extrapolation by characteristic scale motion vectors or the subscale motion vectors from initial field, overlaid the characteristic scale motion vectors (vector); (d) forecasting field (shaded) with characteristic scale; (e) forecasting field (shaded) with characteristic scale overlaid the subscale motion vectors (vector) with 2×2 self-split unit; (g) forecasting field (shaded) with 2×2 self-split unit overlaid the subscale motion vectors (vector) with 3×3 self-split unit; (i) forecasting field (shaded) with 3×3 self-split unit overlaid the subscale motion vectors (vector) with 4×4 self-split unit; (k) forecasting field (shaded) with 4×4 self-split unit overlaid the subscale motion vectors (vector) with 8×8 self-split unit; (f, h, j, l) initial field (shaded) overlaid the synthetic motion vectors (vector, m·s-1) with (f) 2×2, (h) 3×3, (j) 4×4, (l) 8×8 self-split unit, respectively, on 30 April 2013 |
(2) 将第一步特征尺度区域内的雷达回波整体从t0时刻外推到t1时刻,得到t1时刻预报场回波,其中蓝色框区域为包含目标回波的特征尺度区域,如图 1d。
(3) 将特征尺度区域划分等大小的子区域,在每个子区域内利用t1时刻预报场和t1时刻观测场再次进行交叉相关计算,得到原始的特征尺度区域内部每块子区域的内部移动信息,得到次级尺度的运动场du,dv。图 1e、1g、1i、1k给出了将特征尺度区域自我分裂为2×2,3×3,4×4,8×8个单元区域时对应的次级尺度运动速度场,随着次级尺度的不断降低,回波内部的移动信息不断被细化出来。
(4) 将第一步得到特征尺度的运动矢量场u0,v0和第三步得到的内部子区域的内部运动矢量场du,dv进行合成,从而得到更新的运动矢量场u,v。图 1f、1h、1j、1l给出对应自我分裂为2×2,3×3,4×4,8×8个单元区域的次级尺度运动场在上一级尺度合成运动场的基础上得到的合成运动场,随着内部尺度不断细化,合成运动场在特征速度的基础上不断调整,体现在雷暴内部在不同区域逐渐地具有不同的速度。
(5) 循环迭代第二步骤至第四步骤,通过不断内部分裂,在大尺度的运动矢量场的基础上,不断优化得到次尺度的运动矢量场,直到得到最后外推运动矢量场。
若雷达回波前后的形状和强度不变,理论上ATREC方法通过不断迭代,可以使得t1时刻预报场和t1时刻观测场完全重合,最后将得到完美的合成运动场,以用于外推临近预报。但是由于雷达回波前后总是存在一定的变化,所以ATREC方法通常只能使得前后时次的回波无限接近,其相关系数会达到某一特定的极值,而迭代中的次级尺度运动场du, dv也将逐渐趋于0。
由于不同尺度的雷达回波运动特征是各不相同的:特征尺度的运动场起整体主导作用,但是运动场比较单一;次级尺度的运动场能够刻画回波内部的运动信息,有利于优化运动场细节和提高精度,但是有时候也存在内部的次级尺度运动场与整体的特征尺度运动场存在较大的偏差,特别是当雷达回波的结构纹理比较均匀时,可能导致小尺度的运动矢量“错乱”或者“失真”,所以在优化雷暴内部运动场细节以提高精度的同时,要优先保证外推运动矢量场的连续性,否则容易导致外推回波的形状随着预报时长增加而发生显著形变。由于ATREC方法主要采用逐级迭代的方式来逐渐细化外推运动场,所以在每次迭代进行矢量合成时,可以很方便地对合成运动场进行质量控制,具体措施包括:(1)当次级尺度的矢量方向与上一级的合成矢量方向相差超过20°时,次级尺度的运动矢量场将被忽略,该区域依然采用上一级的合成矢量;(2)采用Cressman权重插值对运动矢量场进行连续性平滑。
为了便于实际应用,减少计算量,本文采用一定判断条件来迭代中止,主要包括采用三个方面:(1)当自我分裂的子区域小于10 km×10 km时,因为太小的小尺度运动信息有可能干扰雷暴回波的主体移动;(2)当次级尺度的平均相关系数与上一级尺度的平均相关系数的差值趋于接近0时;(3)当迭代得到次级尺度的运动场du,dv的平均值趋于0时。
ATREC方法的主要特点是:(1)不采用固定的跟踪单元大小,而是依赖具体回波的大小来划分跟踪单元大小,故而不用像传统的TREC类方法那样需要根据当地回波平均尺度或者人为经验来划分跟踪单元的大小,具有很强的客观分析能力;(2)雷暴内部的移动信息通过跟踪区域不断自我分裂来获得,次级尺度的运动场信息在上一级尺度的运动场基础上优化改进,由大尺度运动场逐渐细化出小尺度运动场,所以在融合雷暴特征尺度的系统性运动和雷暴内部的次级尺度运动时,能够在保证运动矢量场平滑同时尽可能兼顾雷暴内部的移动信息。
3 不同类型个例检验评估本节通过不同尺度、不同类型的经典天气个例来分析ATREC方法的特性和实际预报能力。针对具体的个例,引入MTREC方法或TREC方法进行对比试验,并通过预报评分给出ATREC方法的效果评估。
3.1 检验评估方法为了定量评估ATREC方法外推的预报效果,引入Dixon and Wiener (1993)所使用列联表法,得到命中率(POD)、虚假警报率(FAR)和临界成功指数(CSI)来对ATREC方法效果进行检验评估。将预报数据和雷达实况数据逐个格点对比:设定检验评分的阈值为30 dBz,如果实况格点数据和预报格点数据都大于该阈值,则判定该格点预报成功(n成功);若实况格点数据大于阈值而预报格点数据小于阈值,则判定该格点空报失败(n失败);若实况格点数据小于阈值而预报格点数据大于阈值,则该格点是虚假警报(n虚警)。计算公式如下:
| $ P O D=\frac{n_{\text {成功 }}}{n_{\text {成功 }}+n_{\text {失败 }}} $ | (2) |
| $ F A R=\frac{n_{\text {失败 }}}{n_{\text {成功 }}+n_{\text {失败 }}} $ | (3) |
| $ C S I=\frac{n_{\text {成功 }}}{n_{\text {成功 }}+n_{\text {失败 }}+n_{\text {虚警 }}} $ | (4) |
预报每隔6 min进行一次输出,根据实况和预报进行比对得到检验评分。
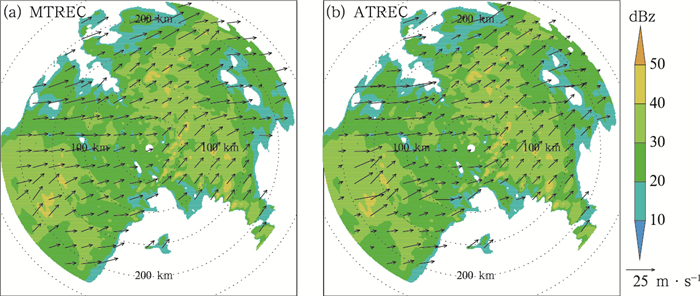
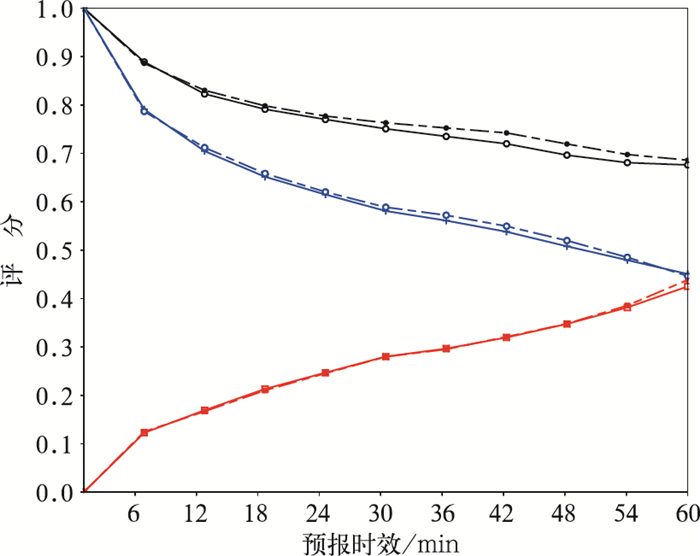
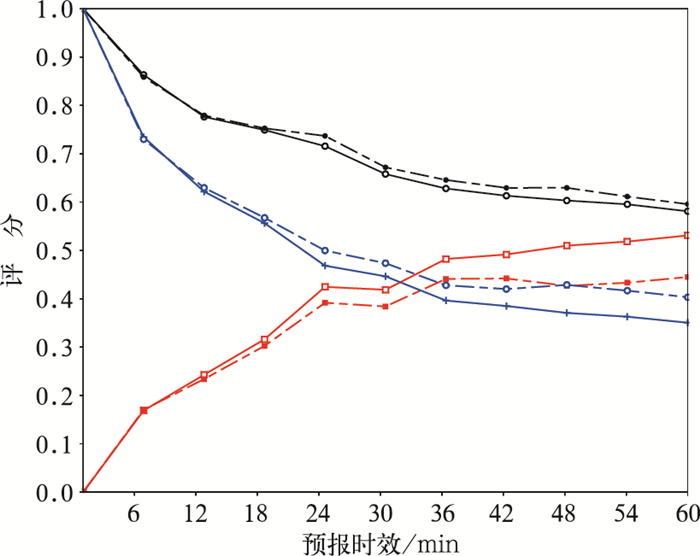
3.2 飑线个例首先以第二部分的飑线个例为例,通过摩尔邻域法识别出飑线的边界后进行ATREC算法计算,由于飑线的整体运动比较一致,所以ATREC算法通过自我分裂为2×2的单元时,就达到迭代中止条件,得到ATREC方法运动场如图 2b。作为对比试验,MTREC方法大尺度的跟踪区域取50 km×50 km,区域间隔取25 km,小尺度的跟踪区域取25 km×25 km,区域间隔取10 km,MTREC方法得到对应运动场如图 2a。对比两种方法得到的运动场,ATREC方法运动场整体偏东移动,而MTREC方法运动场整体向东北偏东方向移动,具有一定偏北的分量。MTREC方法本质上就是进行两次不同尺度的TREC算法计算再做合成,其效果跟TREC方法一样受到跟踪区域大小的影响。当跟踪区域的尺度小于对流尺度时,总会一定程度上平滑掉部分系统性的移动。所以ATREC方法具有优越的灵活性,其跟踪区域的大小首先采用与对流尺度相匹配的特征尺度区域,在系统性移动的基础上,再细化出对流系统内部不同区域的移动矢量场,同时可以通过设置质量控制,在迭代过程中过滤掉与回波整体运动不协调的次级尺度信息。从60 min的预报结果来看,图 3中MTREC方法和ATREC方法都能保持飑线的整体形状和强度,但是从40 dBz以上的区域分布来看,两者预报位置存在一定偏差,MTREC方法相对实况偏慢,ATREC方法则与实况更为接近。如图 4所示,从预报评分来看:两者的预报效果都是随着预报时间延长而递减,ATREC方法的POD和CSI随预报时效降低,FAR随着预报时效升高,但是ATREC方法的检验评分整体都明显优于MTREC方法。
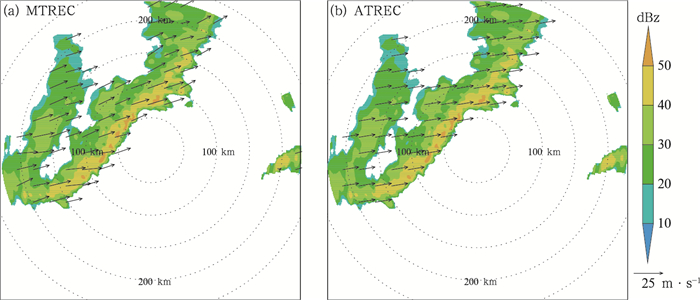
|
图 2 2013年4月30日04:00 UTC,3 km高度回波(阴影)叠加(a)MTREC方法,(b)ATREC方法反演得到运动场(矢量) Fig. 2 Retrieved motion vectors (vector) of (a) MTREC, (b) ATREC overlaid radar reflectivity (shaded) at 3 km height at 04:00 UTC 30 April 2013 |
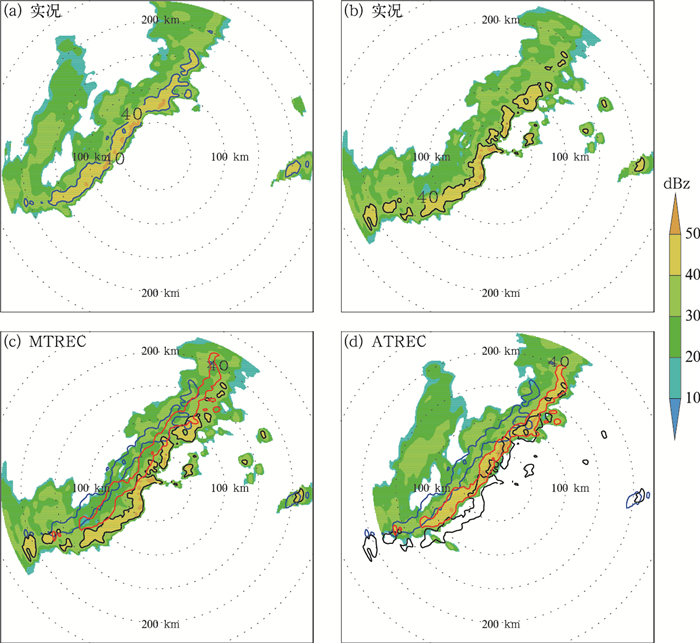
|
图 3 2013年4月30日(a)04:00 UTC,(b)05:00 UTC雷达回波(阴影),(c)MTREC,(d)ATREC外推60 min预报 (反射率40 dBz以上回波落区,蓝线为初始场,黑线为实况场,红线为预报场) Fig. 3 The case on 30 April 2013: observed reflectivities (shaded) at (a) 04:00 UTC and (b) 05:00 UTC (shaded), 60 min nowcasts of (c) MTREC (shaded) and (d) ATREC (shaded) (contours enveloped the area with reflectivity over 40 dBz, blue contour: initial field, black contour: observed field, red contour: forecasting field) |
|
图 4 2013年4月30日个例,外推预报60 min评分 (黑线为POD,红线为FAR,蓝线为CSI,实线为MTREC方法,虚线为ATREC方法) Fig. 4 Evaluation scores based on the case on 30 April 2013: POD (black line), FAR (red line) and CSI (blue line) within 60 min forecasts for MTREC (solid line) and ATREC (dashed line) |
2016年5月20日个例是一次大范围的混合降水过程,大片弱回波中隐嵌着各种不同尺度对流单体,如图 5所示,雷达区域内的东北象限和西南象限存在两片相对较强的回波。从MTREC方法反演的结果(图 5a)可以看出,两片较强回波的移动速度相对较大,方向也略有差异,两片回波之间存在明显的速度场过渡带。而从图 5b来看,ATREC方法反演出来的运动场也基本反映出两片强回波区域的速度特征以及两片强回波之间速度过渡带。由于回波范围比较大,存在大量弱回波的混合降水,边界模糊复杂,故而对于这样的降水类型,像质心法这一类的形状识别的方法会受到严重限制。同样,对于需要用边界识别来确定特征尺度区域的ATREC方法,也具有一定挑战性,但是由于ATREC方法并不像质心法类算法那样需要明确对流系统的边界来确定质心,ATREC方法对于确定边界的要求比较宽松,只要覆盖目标回波的大致区域即可,甚至可以在原有边界基础上,适当扩大一些,所有具有较强的适应性。
从预报60 min的结果来看:虽然实况回波范围比较大,但是总体强度偏弱,40 dBz以上的区域的高反射率区域分布比较零星,且生消比较快,其中东南象限的回波有所发展,东北象限的回波有所减弱,基于外推理论的MTREC方法和ATREC方法都无法解决好回波生消的问题,但是两种方法都预报出了回波的整体移动趋势(图 6)。从预报评分来看,MTREC方法和ATREC方法的效果比较接近,FAR基本保持一致,而ATREC的POD和CSI要略优于MTREC方法(图 7)。
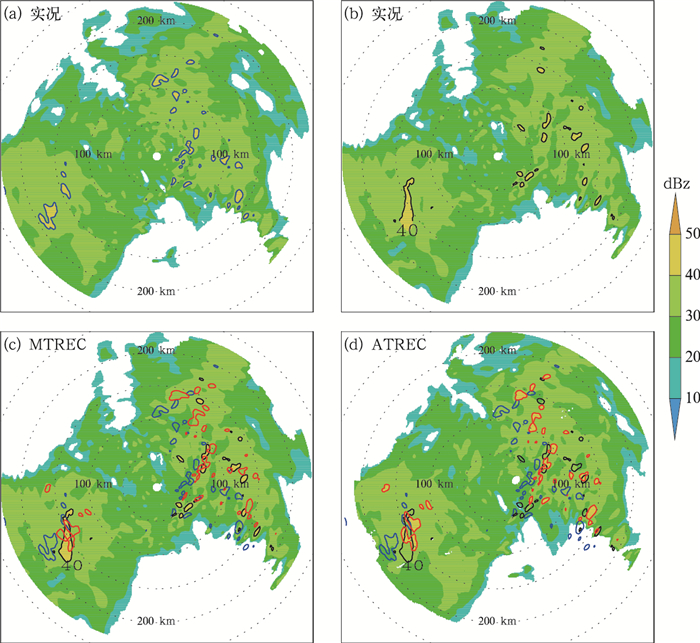
|
图 6 2016年5月20日(a)05:48 UTC,(b)06:48 UTC雷达回波(阴影),(c,d)同图 3c,3d Fig. 6 The case on 20 May 2016: Observed reflectivities (shaded) at (a) 05:48 UTC and (b) 06:48 UTC, (c, d) same as Figs. 3c, 3d |
3.4 多单体个例
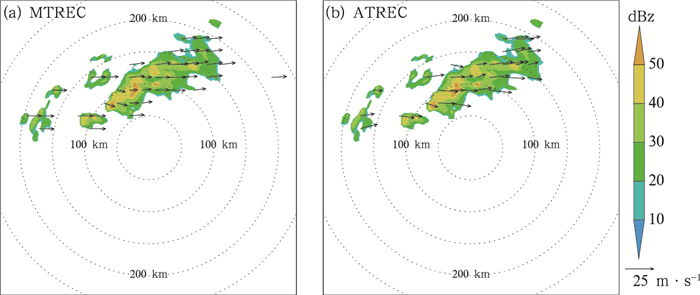
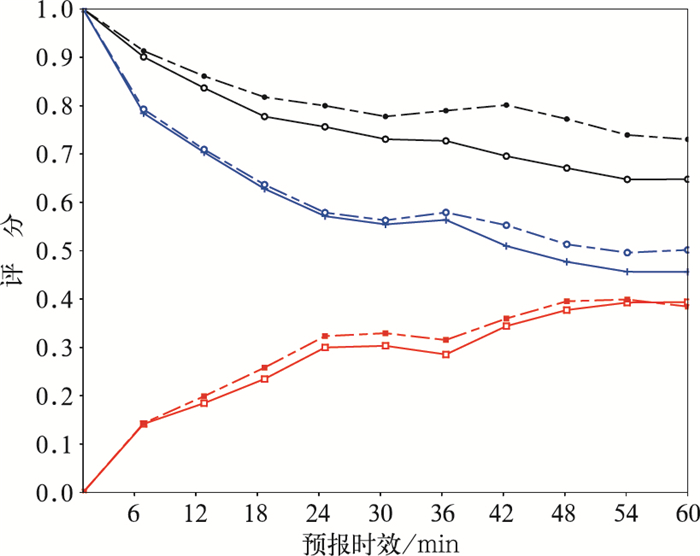
2016年5月9日的多单体个例由若干孤立或者连续的对流单体组成,整体偏东移动。如图 8所示,MTREC方法得到运动场整体比较平直,而ATREC方法得到运动场在多单体雷暴内不同的回波区域上的速度略有不同,特别是多单体周边若干孤立的对流单体,也具有一定的速度差异,这是因为MTREC是根据固定的区域来计算跟踪速度场,而ATREC方法是跟踪单一整块的回波。从实况图 9a和9b来年,在预报时段1小时内,该多单体雷暴虽然形状和强度有所改变,但是还能维持回波总体上的连续性。从预报结果来看,两种方法基本能保持回波的整体形状和强度,MTREC方法1小时后的预报场相对比实况场整体偏慢,而ATREC方法的结果跟实况匹配更好,特别是ATREC方法得到的预报场与实况场在40 dBz以上的区域重合面积更大(图 9c、9d)。从预报评分的结果来(图 10),ATREC方法的效果也要明显优于MTREC方法。
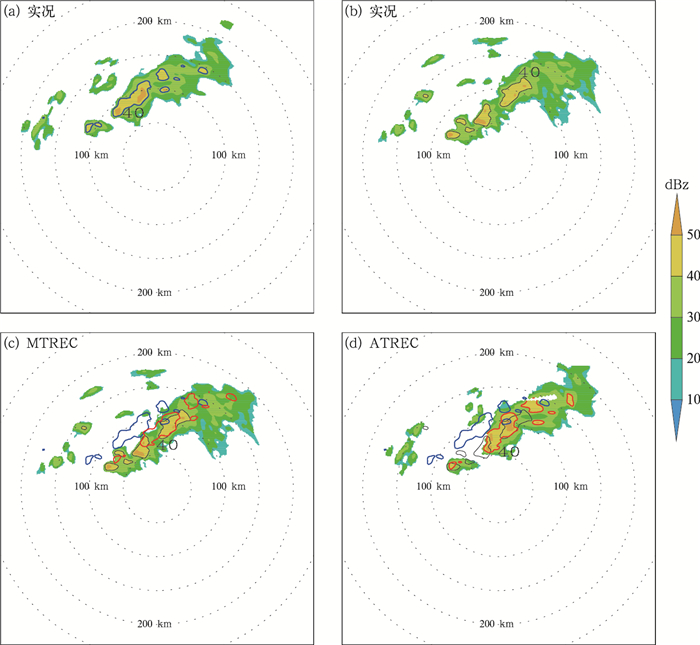
|
图 9 2016年5月9日(a)08:30 UTC,(b)09:30 UTC雷达回波(阴影),(c,d)同图 3c,3d Fig. 9 The case on 9 May 2016: observed reflectivities (shaded) at (a) 08:30 UTC and (b) 09:30 UTC, (c, d) same as Figs. 3c, 3d |
3.5 对流单体个例
在实际应用当中,TREC类方法并不太适合对流单体。因为通常TREC类方法的跟踪区域不能取得太小,当跟踪区域取成固定时,小尺度的对流单体由于在跟踪区域内有效的观测样本数量比较少,往往难以达到TREC算法预设的样本阈值,从而被忽略。特别是MTREC方法需要将大尺度的跟踪区域取得比较大,甚至MTREC方法使用的小尺度的跟踪区域都比对流单体本身的尺度都要大,根本无法先反演系统性运动,再反演对流单体的内部运动。所以本文在对流单体个例分析中,采用TREC方法作为对比试验,跟踪区域的大小与MTREC方法所使用的小尺度跟踪区域保持一致,即跟踪区域大小为25 km×25 km,区域间隔为10 km,且为适应对流单体较小,将TREC算法对于跟踪区域内样本数量的阈值降低到10%。由于ATREC方法不需要预设跟踪区域的大小,所以ATREC方法可以不考虑对流尺度的因素而直接进行计算, 进而得到(图 11)试验结果。
由图 11可以看出ATREC方法得到运动基本保持整体一致的速度,这是因为对流单体尺度本身就比较小,且其移动比较一致,所以ATREC方法达到迭代中止条件,没有进一步自我分裂,反演更次级尺度的运动信息。而TREC方法运动场在对流单体内不同的区域依然在方向和速度上略有差异,这里主要因为是TREC方法采用固定网格区域对流单体进行划分后再进行跟踪算法求运动速度,所以包含对流单体不同部分的区域将具有不同的速度。由于对流单体生命周期比较短,如图 12所示仅仅半个小时,目标对流单体左侧就开始消散,形状和强度都有一定变化,所以这里对于对流单体的个例分析,预报时间取为30 min。从预报结果来,两者预报的回波与实况都比较接近,只是形状略有差异,而从预报评分来,如图 13所示ATREC方法在30 min预报的检验评分总体还是略优于TREC方法。
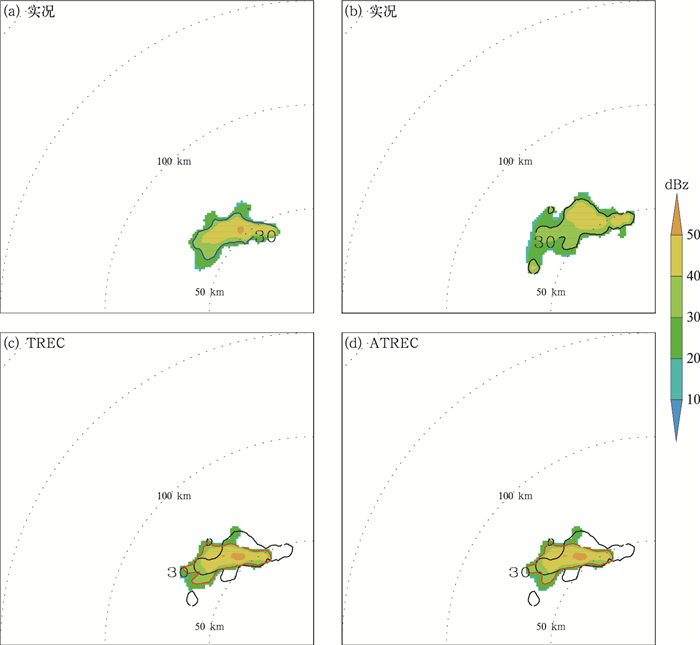
|
图 12 2016年6月26日(a)06:18 UTC,(b)07:18 UTC雷达回波(阴影),(c,d)同图 3c,3d,但为外推30 min Fig. 12 The case on 26 June 2016: observed reflectivities (shaded) at (a) 06:18 UTC, and (b) 07:18 UTC, (c, d) same as Figs. 3c, 3d, but for 30 min nowcasts |
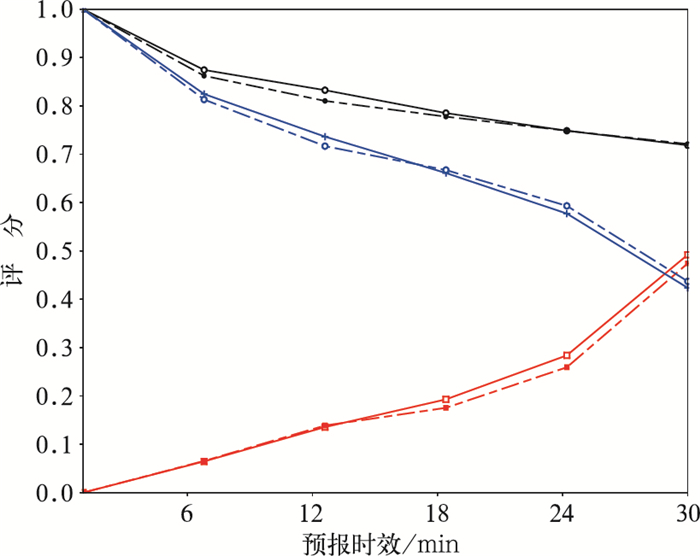
|
图 13 同图 4,但为2016年6月26日个例,外推预报30 min评分 Fig. 13 Same as Fig. 4, but for the case on 26 June 2016 within 30 min forecasts |
为了进一步证明ATREC方法在实际业务中可行性和有效性,本节选取2016年4月1—30日总共128个个例进行统计检验评估。为了保证客观性,从4月1日00 UTC开始,每隔3 h使用ATREC方法和MTREC方法进行一次外推对比试验,预报时效为60 min。虽然ATREC方法不受雷达回波的具体大小的影响,但是由于MTREC采用固定大小跟踪单元,当雷达回波面积太小,跟踪单元中有效的数据格点数占跟踪单元内总格点数的百分率低于60%阈值时,MTREC方法算法会受到一定程度影响。所以为了确保MTREC方法与ATREC方法具有可对比性,当雷达回波面积小于50 km×50 km ×60%时,该次个例将被忽略,不进行统计分析。此外,在预报时效60 min内,雷达回波完全消散的个例也将被忽略统计。
最后得到有效个例总共128个,按照第3节的方法,将阈值设为30 dBz并计算检验评分,通过统计,得到各自检验评分的平均值(图 14)。图 14表明:ATREC方法的平均检验评分明显优于MTREC方法,ATREC方法可以有效地应用于实际业务当中,且具有较高预报精度。
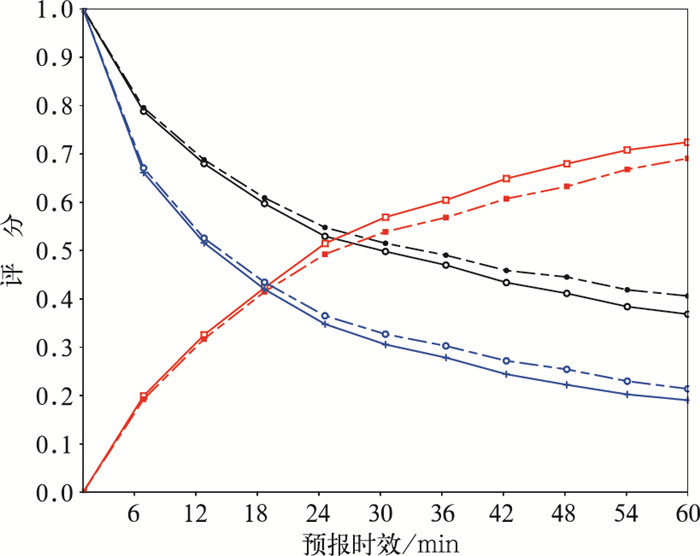
|
图 14 同图 4,但为基于2016年4月总共128个个例进行外推预报60 min的检验评分平均值 Fig. 14 Same as Fig. 4, but for mean evaluation scores based on 128 cases in April 2016 |
ATREC方法与MTREC方法等其他交叉相关跟踪类算法在基础原理上是一致的,其预报效果都具有一定的上限。但是从理论上,ATREC方法的预报精度涵盖MTREC方法这类使用固定大小追踪单元跟踪外推算法的预报精度上限。因为传统的MTREC方法或TREC方法其实可以看做ATREC方法的特例,传统的TREC方法相当于把整个回波场作为特征区域,再采用固定大小的单元进行了一次分裂,而MTREC方法相当于进行大尺度和小尺度两次分裂和一次迭代合成,所以ATREC方法在理论上对这类采用固定大小的TREC类方法具有一定的兼容性。
同时需要指出,虽然ATREC方法理论上可以通过无限迭代、细化运动场,达到最理想的外推矢量场,但是在实际应用中我们需要设置一定的迭代中止条件来方便应用。ATREC方法的自我分裂次数,最小的分裂尺度和相关系数阈值的设定,在一定程度上会限制了ATREC方法达到理论上的精度上限。MTREC方法或者TREC方法采用固定大小的跟踪单元,虽然其大小是基于统计或人为经验设定的,但是如果其跟踪单元的尺度恰好与对流系统的回波尺度本身是比较协调一致的,其外推预报也可以达到比较好的效果,甚至个别的个例比本文中目前使用特定迭代中止条件的ATREC方法评分可能还要高一点,但是这是因为ATREC方法在实际应用中受到迭代中止条件的限制,不能无限分裂细化,其理论精度受到一定的限制导致的。所以ATREC方法在理论上具有非常高的预报精度上限,也具有较强的灵活性,在实际的临近预报应用当中,可以通过设置一定的迭代中止条件来兼顾临近预报的计算快速性和预报准确性。
5 结论与讨论本文在交叉相关算法和摩尔邻域跟踪算法的基础上,提出了ATREC方法,并且通过不同类型、不同尺度的个例分析、对比试验和基于统计实验的综合检验评估,验证了ATREC方法的可行性和有效性,结论和讨论如下:
(1) ATREC方法能够根据对流回波的边界识别,自动选取对应大小尺度的跟踪区域,能够有效解决目前TREC类方法预设固定大小的跟踪区域所带来的问题,例如对系统性运动的削弱、小尺度系统的不适用性等。ATREC方法在雷达回波总体运动场基础上,逐级衍化出不同次级尺度的移动信息,最后将特征尺度的特征运动场和各层次级尺度的内部运动场进行合成,所以得到的外推运动场比较平滑且能兼顾不同尺度的移动信息。
(2) 通过对比传统采用固定单元大小的TREC类方法,包括MTREC方法和TREC方法,个例分析表明:针对不同尺度、不同类型的对流天气系统,ATREC方法具有较强的客观分析能力,能够自动反演出各种尺度的对流系统移动信息,既包括整体的系统性的移动信息,也包括各种次级尺度的雷暴内部移动信息。预报评分显示,相对传统的MTREC方法或者TREC方法,ATREC方法在不同尺度、不同类型的对流系统的临近预报中都具有较好的预报能力,且有较强的灵活性、适应性和准确性。通过2016年4月总共128个个例的统计检验评分结果表明:ATREC方法的预报评分整体优于MTREC方法。
(3) 目前ATREC方法在划分次级区域时,还是采用了比较简单的等大小自我分裂的方式,实际上不少对流回波本身形状各异,且内部不同次级尺度的运动场具有不同的运动特性,所以ATREC方法在如何划分次级尺度方面还有改进潜力。另外目前试验只是用到相邻时次的雷达资料做ATREC方法跟踪,若采用多时次的资料进行自适应尺度跟踪,能够得到更多对流系统的移动演化信息(符式红等,2012)。故而ATREC还有进一步升级改进的空间。
曹春燕, 陈元昭, 刘东华, 等, 2015. 光流法及其在临近预报中的应用[J]. 气象学报, 73(3): 471-480. Cao C Y, Chen Y Z, Liu D H, et al, 2015. The optical flow method and its application to nowcasting[J]. Acta Meteor Sin, 73(3): 471-480 (in Chinese).
|
陈雷, 戴建华, 陶岚, 2009. 一种改进后的交叉相关法(COTREC)在降水临近预报中的应用[J]. 热带气象学报, 25(1): 117-122. Chen L, Dai J H, Tao L, 2009. Application of an improved TREC algorithm (COTREC) for precipitation nowcast[J]. J Trop Meteor, 25(1): 117-122 (in Chinese). DOI:10.3969/j.issn.1004-4965.2009.01.015
|
陈明轩, 王迎春, 俞小鼎, 2007. 交叉相关外推算法的改进及其在对流临近预报中的应用[J]. 应用气象学报, 18(5): 690-701. Chen M X, Wang Y C, Yu X D, 2007. Improvement and application test of TREC algorithm for convective storm nowcast[J]. J Appl Meteor Sci, 18(5): 690-701 (in Chinese). DOI:10.3969/j.issn.1001-7313.2007.05.014
|
符式红, 钟青, 寿绍文, 2012. 对多普勒雷达集合交叉相关外推技术的构造与实例检验[J]. 气象, 38(1): 47-55. Fu S H, Zhong Q, Shou S W, 2012. Construction and case verification on Doppler radar ensemble extrapolation of cross-correlation[J]. Meteor Mon, 38(1): 47-55 (in Chinese).
|
王改利, 刘黎平, 2007. 暴雨云团的多尺度识别方法及其在临近预报中的应用[J]. 大气科学, 31(3): 400-409. Wang G L, Liu L P, 2007. A multiscale identifying algorithm for heavy rainfall and application in nowcasting[J]. Chin J Atmos Sci, 31(3): 400-409 (in Chinese).
|
俞小鼎, 郑永光, 2020. 中国当代强对流天气研究与业务进展[J]. 气象学报, 78(3): 391-418. Yu X D, Zheng Y G, 2020. Advances in severe convective weather research and operational service in China[J]. Acta Meteor Sin, 78(3): 391-418 (in Chinese).
|
曾小团, 梁巧倩, 农孟松, 等, 2010. 交叉相关算法在强对流天气临近预报中的应用[J]. 气象, 36(1): 31-40. Zeng X T, Liang Q Q, Nong M S, et al, 2010. Application test of TREC algorithm to severe convective storm nowcasting[J]. Meteor Mon, 36(1): 31-40 (in Chinese).
|
郑永光, 张小玲, 周庆亮, 等, 2010. 强对流天气短时临近预报业务技术进展与挑战[J]. 气象, 36(7): 33-42. Zheng Y G, Zhang X L, Zhou Q L, et al, 2010. Review on severe convective weather short-term forecasting and nowcasting[J]. Meteor Mon, 36(7): 33-42 (in Chinese).
|
Bowler N E H, Pierce C E, Seed A, 2004. Development of a precipitation nowcasting algorithm based upon optical flow techniques[J]. J Hydrol, 288(1/2): 74-91.
|
Dixon M, Wiener G, 1993. TITAN: thunderstorm identification, tracking, analysis, and nowcasting-a radar-based methodology[J]. J Atmos Ocean Technol, 10(6): 785-797. DOI:10.1175/1520-0426(1993)010<0785:TTITAA>2.0.CO;2
|
Fulton R A, Breidenbach J P, Seo D J, et al, 1998. The WSR-88D rainfall algorithm[J]. Wea Forecasting, 13(2): 377-395. DOI:10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2
|
Gonzalez R C, Woods R E, Eddins S L, 2004. Digital Image Processing Using MATLAB[M]. Pearson Prentice Hall.
|
Han L, Fu S X, Zhao L F, et al, 2009. 3D convective storm identification, tracking, and forecasting-an enhanced TITAN algorithm[J]. J Atmos Ocean Technol, 26(4): 719-732. DOI:10.1175/2008JTECHA1084.1
|
Horn B K P, Schunck B G, 1981. Determining optical flow[J]. Artif Intell, 17(1/2/3): 185-203.
|
Houze R A Jr, Schmid W, Fovell R G, et al, 1993. Hailstorms in Switzerland: left movers, right movers, and false hooks[J]. Mon Wea Rev, 121(12): 3345-3370. DOI:10.1175/1520-0493(1993)121<3345:HISLMR>2.0.CO;2
|
Johnson J T, Mackeen P L, Witt A, et al, 1998. The storm cell identification and tracking algorithm: an enhanced WSR-88D algorithm[J]. Wea Forecasting, 13(2): 263-276. DOI:10.1175/1520-0434(1998)013<0263:TSCIAT>2.0.CO;2
|
Li L, Schmid W, Joss J, 1995. Nowcasting of motion and growth of precipitation with radar over a complex orography[J]. J Appl Meteor Climatol, 34(6): 1286-1300. DOI:10.1175/1520-0450(1995)034<1286:NOMAGO>2.0.CO;2
|
Lucas B D, Kanade T, 1981. An iterative image registration technique with an application to stereo vision[C]//Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI). San Francisco: Morgan Kaufmann Publishers Inc: 674-679.
|
Rinehart R, Garvey E, 1978. Three-dimensional storm motion detection by conventional weather radar[J]. Nature, 273(5660): 287-289. DOI:10.1038/273287a0
|
Tuttle J D, Foote G B, 1990. Determination of the boundary layer airflow from a single Doppler radar[J]. J Atmos Ocean Technol, 7(2): 218-232. DOI:10.1175/1520-0426(1990)007<0218:DOTBLA>2.0.CO;2
|
Wang G L, Wong W K, Liu L P, et al, 2013. Application of multi-scale tracking radar echoes scheme in quantitative precipitation nowcasting[J]. Adv Atmos Sci, 30(2): 448-460. DOI:10.1007/s00376-012-2026-7
|
Wilson J W, Crook N A, Mueller C K, et al, 1998. Nowcasting thunderstorms: a status report[J]. Bull Amer Meteor Soc, 79(10): 2079-2100. DOI:10.1175/1520-0477(1998)079<2079:NTASR>2.0.CO;2
|
 2022, Vol. 48
2022, Vol. 48