引言

现代天气预报在数值预报模型的支持下，正在快速发展，但由于资料同化方法、地理分辨率的限制，数值模式的应用仍有较大的提升空间。早期国际上常用模式输出统计(MOS)等技术，使用数值预报与观测数据，通过线性回归方法推导预报方程，评估表明，MOS方法在最高气温等要素预报中能显著减小数值预报的误差，是有效的客观预报技术(Glahn and Lowry, 1972)，美国国家气象局将其进行了业务化(Klein and Glahn, 1974)。大气本身是非线性的动力系统，其对初始条件非常敏感，增加初始条件的扰动，生成多成员的集合预报方法，也能有效的优化单模型的预报结果(Leutbecher and Palmer, 2008)。根据我国气象部门智能网格预报发展要求，现已在全国范围推行逐3 h精细化网格预报业务。针对数值预报的气温订正，已有较多试验性的研究：智协飞等(2009)分别利用固定训练期超级集合和滑动训练期超级集合方法对北半球中纬度地面气温进行预报试验，发现均有效降低了预报误差，滑动训练期效果更优；李佰平和智协飞(2012)分别利用一元线性回归、多元线性回归、单时效消除偏差和多时效消除偏差平均等订正方法，对ECMWF-IFS的2 m气温预报结果进行订正，能有效地减小地面气温多个时效预报的误差；王敏等(2012)采用非齐次高斯回归技术对国家气象中心区域集合预报系统的2 m温度预报结果进行校准，预报可靠性和预报技巧均显著提高；王婧等(2015)采用平均法、双权重平均法、滑动平均法和滑动双权重平均法对GRAPES_RAFS系统2 m温度预报产品进行偏差订正，结果表明大部分地区的平均误差、均方根误差都有显著降低；冯慧敏等(2016)利用多模式集合平均、消除偏差集合平均、加权消除偏差集合及多模式超级集合方法，对地面逐3 h气温进行多模式集成预报试验，结果表明集成方案对预报效果有不同程度的改善。近几年，基于模式输出统计方法(吴启树等，2016)、滑动双权重平均订正法和空间误差逐步订正法综合订正技术(薛谌彬等，2019)对ECMWF-IFS逐日最高/最低气温进行订正，较好地改善了站点温度的预报质量并应用于业务系统中；曾晓青等(2019)使用温度格点多源融合产品和ECMWF-IFS的2 m温度预报场，采用简单误差订正、误差回归订正等8种方案，进行订正预报试验，对格点、站点的检验结果表明，多种方案都对3~24 h(预报时间间隔3 h)预报有明显的订正作用；王丹等(2019)使用递减平均法和一元线性回归法对ECMWF-IFS的定时最高(低)气温预报误差进行订正，订正后的预报质量有提升，但在较长预报时效不太理想，部分地区订正技巧为负；郝翠等(2019)采用最优集合预报方法对北京市各站1~7 d的日最高气温和日最低气温进行订正，结果表明滑动训练期、优化变量权重两种方案能改善模式固有偏差，其结果优于或与预报员主观预报相当，但在某些局地天气影响下不如主观预报；王在文等(2019)使用相似集合方法对北京快速更新循环数值预报系统的地面要素开展订正试验，并将其与支持向量机的订正效果进行了对比，在有效减小气温预报误差的同时，其计算资源要求更低；盛春岩等(2020)使用气温偏差订正和准对称混合滑动训练期MOS方法集成订正ECMWF-IFS的气温预报，取得较好的效果，但也发现从第3天开始客观方法高温准确率有明显下降趋势；尹珊等(2020)应用滑动平均误差订正方法和历史偏差订正方法，对ECMWF-IFS延伸期2 m温度预报进行误差订正，两种方法在全年各月都有正订正技巧，其中1—3月效果最明显，但无法订正模式对变温时间的预报误差；任萍等(2020)分别基于机器学习方法XGBoost、等权重平均方法、线性回归方法且考虑地形因子影响，构建出多种模型，对北京地区快速循环同化数值预报系统输出的结果进行订正，在包括气温在内的多要素上XGBoost表现最优。

深度学习(deep learning，DL)方法是处理气象大数据的前沿技术。虽然受到一些客观因素的制约，现阶段DL技术无法完全学习到大气运动的物理规律，但累积的数值模式历史预报数据，可处理成为一项有效的数据集输入到DL模型中。当前，从注重数理原理解释到注重动力热力方程求解与人工智能方法相结合，已经取得了重大进展(许小峰，2018)。图像处理单元(GPU)计算技术对比传统中央处理单元(CPU)具有更高效率，给更大规模、更深层次的数据挖掘提供了可能，因此，基于深度学习方法的气温订正技术相比传统MOS方法，能从数值预报中挖掘出更多时间、空间相关信息。

目前，有学者使用DL方法对数值预报结果进行改进。在气温预报的应用上，Li et al(2019)基于模式输出机器学习(MOML)方案，将已有的机器学习回归算法应用到处理后的训练集、测试集中，结果比ECMWF-IFS模式结果和MOS方法更好，尤其是冬季更明显。陈昱文等(2020)基于TIGGE的ECMWF-IFS资料，建立深度学习模型，并对部分站点进行气温误差订正，结果表明机器学习在数值模式预报结果订正中具有较大的应用潜力。门晓磊等(2019)使用基于岭回归、随机森林和深度学习的3种后处理模型，应用多模式预报结果进行逐日气温预报，对比了多种模型的订正效果，发现DL方法在空间分布上效果最好。Han et al(2021)基于U-Net(为生物医学图像分割而开发的卷积神经网络)提出深度学习模型CU-Net，对ECMWF-IFS的2 m温度、2 m相对湿度、10 m风的24~240 h预报进行格点订正，在多个检验指标上都取得了更优的结果，并指出深度学习方法具有从NWP海量数据中直接进行学习从而构建NWP偏差特征的能力。在第二届AI Challenger全球挑战赛中，使用基于时间序列分析、梯度提升树、深度概率预测等AI模型构建的多组集合预报方法，相比之前的相似集合预报方法，显著提高了2 m气温的预报水平(嵇磊等，2019)。

由于对数据获取、模型运行的稳定性要求高等原因，大多数深度学习预报方法仅停留在试验阶段(大多数预报为逐日最高/最低气温预报)，有的标签、验证数据使用了一日2次的模式分析场(或者再分析场)而并非实际观测数据，或者使用较为稀疏的气象站，代表性不足，真正建立预报模型并应用到智能网格预报业务且取得较好效果的先例较少。从2016—2018年国家级网格指导预报、省市级订正反馈网格预报的气温要素检验来看，国家级网格统计预报模型建立后，预报误差呈现出数值模式、国家级、省市订正逐级减小的趋势，体现出智能预报的巨大优势(韦青等，2020)。湖南省位于江南地区西部，地形上东、南、西三面环山，北部海拔稍低，东北部洞庭湖地区为其最主要的南下冷空气输入路径。目前针对湖南地区的气温预报，较少进行系统的评估，更无有效的客观订正方法，从日常预报业务检验看，ECMWF-IFS等数值预报对湖南的气温预报结果存在明显的误差。例如，在湖南西部的雪峰山、西北部的武陵山及南部的南岭部分地区，数值预报平均偏差3℃以上，部分海拔超过800 m的站点平均偏差4℃以上，东部部分低海拔地区也出现了3℃以上的偏差。误差并非简单随海拔变化而线性增长，它受到下垫面、坡向，以及各个层次温度平流等多个气象要素的共同影响，无法使用简单的消除偏差方法去除。本文以改善湖南全省逐3 h气温预报为目标，建立了精细化气温预报流程，并使用气象站观测资料进行结果验证与评估。

1 资料

本研究使用湖南省气象信息中心通过CMACast接收保存的北半球区域ECMWF-IFS高分辨率数值预报模式产品进行训练，模式地面层分辨率为0.125°×0.125°，气压层分辨率为0.25°×0.25°，选取了地面层所有预报要素，以及19个气压层的气温、高度、湿度、风场等要素；训练期为2017年1月1日至2019年12月31日，将2020年1月1日至12月31日的数据作为测试集进行预报评估分析，模式每日00时和12时(世界时，下同)起报。基于逐3 h精细化气象要素预报工作的需要，本文选择了0~84 h，一共27个预报时效的要素预报数据。使用湖南省全境421个气象站(包含国家站和骨干站)逐3 h(分别为00、03、06、09、12、15、18、21时)气温观测数据，数据来源为湖南省气象信息中心CIMISS系统，数据总长度为2017年1月1日至2020年12月31日，其中将2020年的数据作为测试集进行评估与对比分析。

2 模型与方法 2.1 深度学习模型

本文设计了一种适用于气象要素预测订正的深度学习模型，模型使用了多层全连接神经网络模型对数值预报气温订正函数进行拟合。

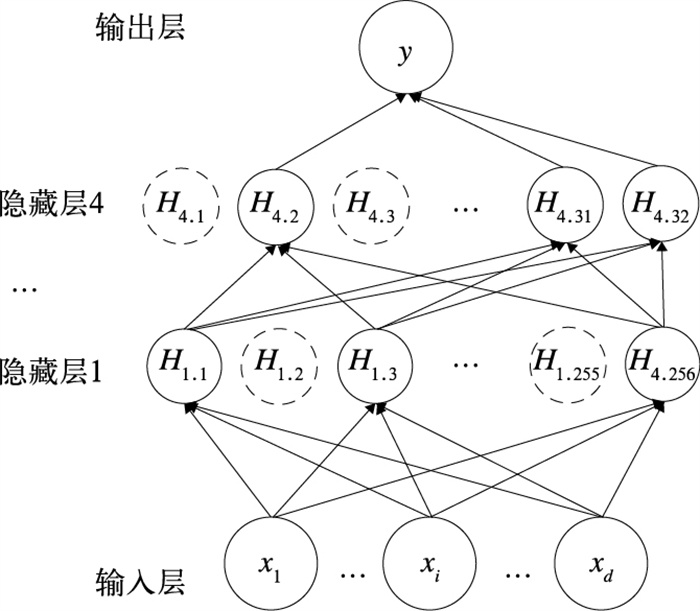
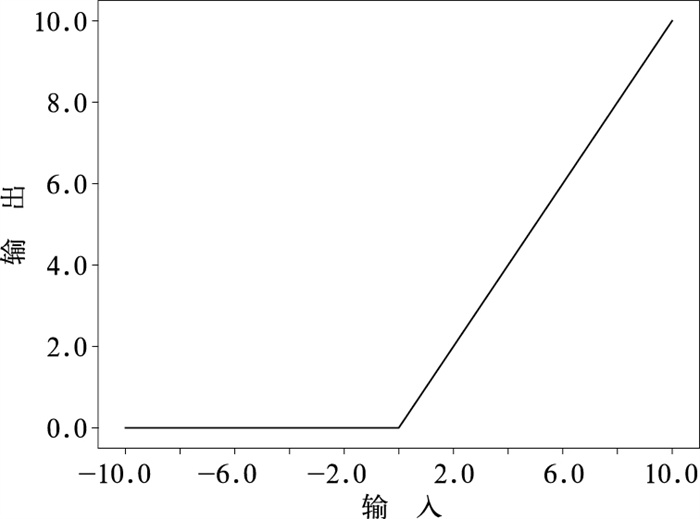
多层全连接网络模型是一种经典的神经网络模型，具有输入层、隐藏层和输出层三种结构。其中输入层和输出层有且只有一层神经元结构，隐藏层可以根据计算量的接受程度设计为多层神经元结构。相邻层之间的神经元全部相互连接，并在每个连接上赋予一个计算权重。每层神经元(除输入层)的输入均为上一层神经元的输入，每个神经元的输出均为上层各神经元的值与相应连接权重的相乘后再相加，并经过激活函数计算之后形成的值。经过前期试验，考虑到计算强度和过拟合问题，最终全连接结构使用了4个隐藏层，分别设置了256、128、64和32个神经元, 全连接网络结构示意图(图 1)中，H_ij为第i个隐藏层的第j个神经元；输入数据为某时刻经过筛选的各个气象要素的值x_i，输出为各个气象要素的综合提取特征y。为避免神经元死亡的问题，本文在初始试验阶段控制、调整了学习率。模型中使用了Dropout技术，在神经网络中丢弃部分隐藏神经元(图 1中表现为虚线圆)，能够避免在训练数据上产生复杂的相互适应。为了模拟天气运动的复杂多样，激活函数一般采用非线性函数，本文使用的是线性整流函数(ReLU)，ReLU具有收敛速度快、效率高、能克服梯度消失等优点。在激活函数ReLU示意图(图 2)中，x轴为上一层神经网络的输入量，进行变换后，y轴为输出的下一层神经元或者神经网络最终结果。

由于天气的演变过程复杂多变，所以模型的选择应该重点考虑提取各个气象要素的时序特征。同时天气预报具有时效性，影响天气变化的气象要素多种多样，所以模型也要考虑输入数据集的大小以及网络训练的时间成本问题。常见的模式后处理方法在对站点要素进行订正预报时，采用单点、多层、多种气象要素因子进行建模。基于这个思路，本文使用全连接神经网络建立了站点的气温预报模型(下文简称为DL模型)，从而减少网络训练时间，以达到快速高效的预报订正效果。在建立模型时，分别按单站、区域建立了多类预报模型，以测试集的订正效果自动优选误差低的模型，尽量避免站点因为样本量过少而出现过拟合。

2.2 数据预处理

本文从数值模式训练集中提取了高空多层的位势高度、比湿、温度、风场等要素和地面单层的气温、降水等要素。先使用最近格点法插值到421个目标站点，再对数据集进行筛查、清洗等相关预处理，使用气象观测阈值过滤或替换奇异值。最终进行标准化处理：使用Z-score算法对数据集进行缩放，公式如下：

$ Z=\frac{x-u}{\sigma} $

(1)

式中：x为需被标准化的原始数据值，u为气象要素的总体数据均值，σ是总体数据的标准差。

然后将数据归一处理到0~1，公式如下：

$ x^*=\frac{x-X_{\min }}{X_{\max }-X_{\min }} $

(2)

式中：X_max为样本数据的最大值，X_min为样本数据的最小值。

本文中使用的每个样本包含因子198个(实际训练中有经过调整和筛选)，2017—2019年数据集共有样本22 457 196个，使用经过筛查、清洗后的数据进行建模，其中86%的数据作为训练集, 14%的数据作为验证集；以收集到的2020年实际预报业务数据作为测试集。分配如表 1所示。

2.3 检验方法

均方根误差(RMSE)是回归问题的常用性能指标，不仅可以作为深度学习模型中的损失函数，还可以明确地指示订正效果优劣，公式如下：

$ R M S E=\sqrt{\frac{1}{N_{\mathrm{F}}} \sum\limits_{i=1}^{N_{\mathrm{F}}}\left(F_i-O_i\right)^2} $

(3)

式中：N_F为预报总站数，i为预报站标识，F_i为第i站预报值，O_i为第i站观测值。

改善率I是订正前后的均方根误差的差值相对原预报均方根误差的比值，公式如下：

$ I=\frac{R M S E_{\mathrm{DL}}-R M S E_{\mathrm{EC}}}{R M S E_{\mathrm{EC}}} $

(4)

式中：RMSE_EC、RMSE_DL分别为ECMWF-IFS、DL模型的均方根误差。

3 订正效果

从2020年1月1日开始业务数据输出站点预报订正数据，同时与同期ECMWF-IFS输出的2 m气温(使用最近格点插值到421个站点)进行对比分析。本文重点分析气温的均方根误差以及订正预报的改善率(订正前后均方根误差的差值与订正前的均方根误差之比)。由于业务需要，使用B-样条基函数插值得到逐3 h预报产品，并制作了逐日的最高、最低气温。

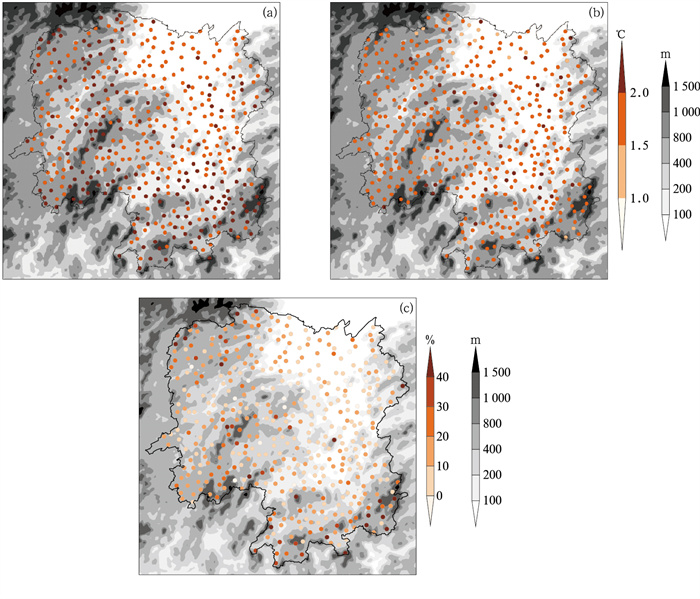
3.1 整体误差的空间分布

0~84 h的ECMWF-IFS原始预报的全省平均RMSE为2.16℃(图 3a)。结合湖南省地形可以看出，西北部的武陵山区、西南部的东北—西南向的雪峰山脉周边、南部的南岭山脉及大部分海拔超过400 m区域，平均RMSE在2.0℃以上，海拔100 m以下大部分地区为1.5~2.0℃。

DL模型订正后的全省平均RMSE为1.78℃，从全省地理分布上看，误差值分布较为均匀，大部分地区为1.5~2.0℃，少量高海拔地区及个别平原地区站点达到2.0℃以上(图 3b)。

从所有订正时效(0~84 h)进行的均方根误差统计上来看，全省范围均方根误差平均减小了15.6%。结合地形分析改善率的空间分布(图 3c)，改善最明显的地区位于湖南省西部和南部山区，部分高海拔地区达到20%~30%，湘西南(雪峰山地区)、湘西北(武陵山地区)、南部(南岭地区)等山地站点的幅度最大，少数站点达到50%~70%；极少数站点(10个站)改善率为负，但控制在10%之内。由于数值预报初始场依赖各类观测资料同化，而资料在复杂地形存在系统误差等原因，导致数值预报对某些高海拔地区的预报存在偏差。

经统计发现，随海拔高度的增加，改善率有明显的上升趋势(表 2)：海拔400 m及以下站点共347个，占总站数的82.4%，平均改善率为13.5%，但也有10个站平均改善率为负(经过深入查看，RMSE增大是因为8月、12月实时数据源切换出现了单位不一致的问题)；海拔400~800 m的站点占总站数12.1%，平均改善率为19.4%；海拔1200 m以上大部分站点改善率达50%以上。改善率与海拔高度呈正相关，经计算得到相关系数为0.560。改善率最高的3个站为大围山站(72.6%，海拔为1378 m)、南岳站(69.6%，海拔为1265.9 m)、雪峰山站(67.8%，海拔为1420 m)。前文中已提到，误差的变化并非随海拔线性增长，海拔只是造成误差的众多因素之一，从误差分布上也可清晰看到DL预报在东部平原地区也存在一些改善不明显的站点。

3.2 不同预报时间的差异

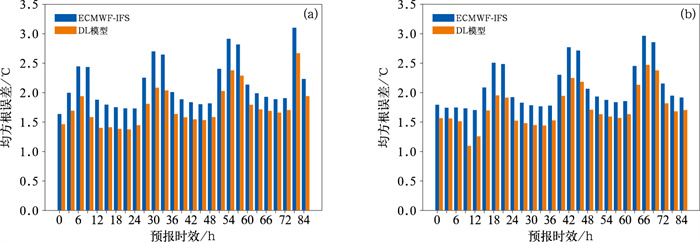
从00时和12时起报的结果(表 3)综合来看，气温预报的平均RMSE有明显的日变化，每日06时对应的时效误差达到最大(两个起报时次平均误差ECMWF-IFS为2.78℃，订正后为2.27℃，减小了0.51℃)，每日21时对应的时效误差最小(两个起报时次平均误差ECMWF-IFS为1.79℃，订正后为1.46℃，减小了0.33℃)。随着预报时效的增加(图 4)，每天对应时间的RMSE也在缓慢增加，在每日06时、09时，可以看到ECMWF-IFS预报的RMSE明显偏高，而DL模型RMSE的订正幅度也最大(达0.50℃左右)；不同起报时间(00时和12时)的预报误差也有不同，但日变化规律基本一致。

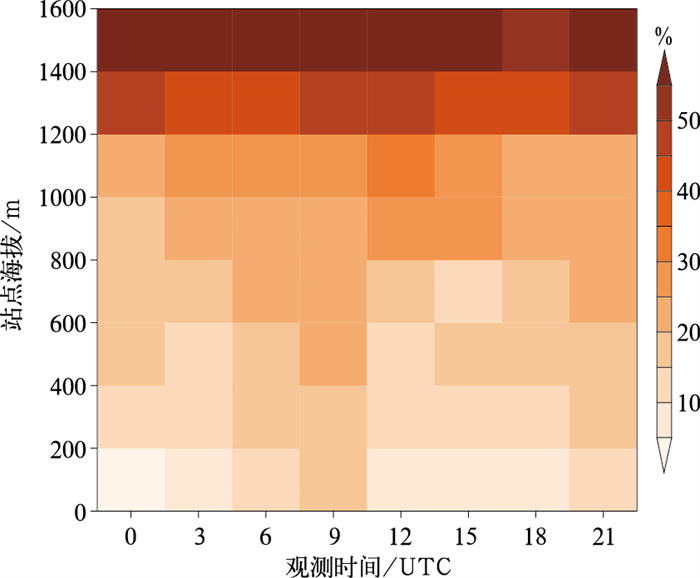
结合海拔高度与观测时间(图 5)，可以发现预报误差基本遵从海拔越高、DL模型对数值预报的改善越明显的规律，但在不同海拔上，改善率具有不同的日变化特征。其中：海拔1200 m以上改善率最高的是00、09、12、21时，平均达40%以上，800~1000 m则在日落以后改善幅度最高，800 m以下地区以每日午后(06时、09时)为主。

从所有站点的统计可以得出，每天06时和09时的误差改善率最高，本文选取这两个预报时间的误差改善率，分析其地理分布。午后时段(图 6a)，改善最明显的是海拔200 m以上地区，大部分误差降低20%以上，傍晚(图 6b)改善率更高，很多午后改善不明显的海拔100 m以下地区(东部平原为主)，改善率达到20%以上。

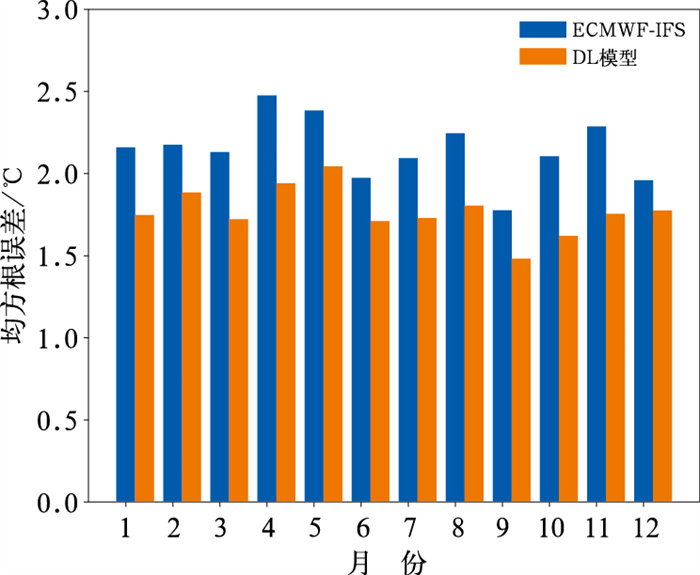
在同年的不同月份，数值预报与DL模型的预报误差也有变化(图 7)：ECMWF-IFS只有6、9、12月平均RMSE < 2℃，其他月份均>2℃，DL模型仅5月平均RMSE>2℃，其他月份均 < 2℃；ECMWF-IFS在4月的平均RMSE最高为2.48℃(DL订正后为1.94℃)，5月RMSE为2.38℃(DL订正后为2.04℃)，说明4月、5月预报难度较大。每个月，DL模式都有明显的订正效果，其中10月、11月(秋季)其对数值预报的改善率最高(超过23%), 其次是3月、4月(春季，20%左右)，12月最低(9%)。

从全年所有日期的全省所有站RMSE变化趋势(图略)来看，两个产品的误差变化趋势基本一致。DL订正方法在绝大部分时间对于ECMWF-IFS数值预报结果进行了有效改善，特别是在3、4、10、11月改善较为明显。

3.3 寒潮降温过程检验

2020年12月29日湖南省出现一次寒潮降温天气过程，此次过程为明显的转折天气：冷空气从湘东北洞庭湖地区南下影响全省，其中29日00时至30日00时，全省大部分地区24 h最高、最低气温相比前一日下降8~10℃，最低气温降至0℃左右。数值模式对降温幅度有较好的体现，但准确率不够，而基于深度学习方法订正后的预报，准确率有明显的提升。

从此次过程统计上(表 4)看，过程3 d全省站点高、低温准确率(误差2℃以内)和逐3 h均方根误差都是DL模型占优势(除了第3天低温准确率ECMWF-IFS表现稍好)；其中：第2天、3天的高温准确率，DL提高了近20个百分点，第1天低温准确率，DL模型从49.0%提升至80.7%，优势非常明显。

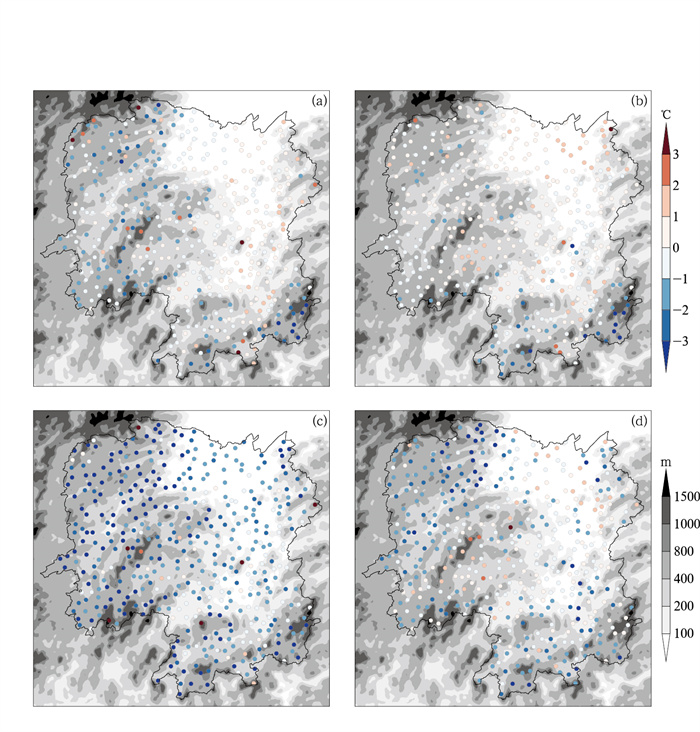
以第1天误差分布(图 8)为例：ECMWF-IFS在湘西、湘东南地区(山地为主)部分站点高温预报偏低2~3℃，DL模型在西部地区订正较好，将大部分地区的偏差控制在±2℃以内，但在东南部山区的预报的订正提升效果不明显，在东北部平原地区甚至比ECMWF-IFS预报偏高；从低温误差分布上看, ECMWF-IFS在全省大部分地区预报偏低2℃，局地偏低3℃以上，DL模型将大部分地区的误差控制在±2℃以内，效果较明显。

DL订正在减小系统性误差的同时，因为受“学习到的经验”影响，对转折天气可能也有负向订正，对其极端性考虑不够(例如第2天降温最显著的东部平原地区气温预报偏高，第3天低温准确率低于ECMWF-IFS)。此外，经过分析同时段ECMWF集合预报的50个扰动成员，发现每个单独站都存在理论上最优成员，其对逐3 h气温、日高低温的准确率接近100%，订正方法对原始预报的改善幅度仍不及理想中的最优集合成员(但不同条件下最优成员的选取值得研究)。

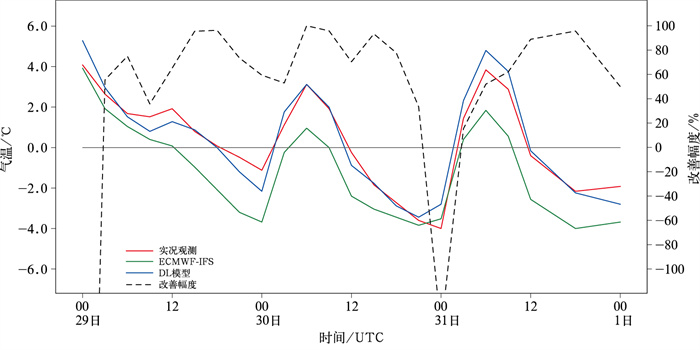
岳阳国家基本气象站位于湖南省东北部洞庭湖平原地区，是冷空气直接影响、降温显著的地区。从单站逐3 h预报、观测时序中(图 9)可以看出，相对实况观测(红色折线)，ECMWF-IFS(绿色折线)的预报偏低，特别是每天日出前的最低气温偏差明显，大部分时次，DL模型(蓝色)预报值比ECMWF-IFS更接近观测值，改善幅度(黑色虚线)为正且大多在50%以上。也有个别时次DL模型误差稍大，但也在可接受的范围内。

此次过程, DL模型在逐3 h预报上，RMSE减少了0.2℃左右，说明逐3 h预报也是气温预报的难点。在实际业务应用中，预报员将偏差明显的个别站点进行了手工订正，起到了最终把关作用。

4 结论与讨论

本文从站点预报实际应用的角度，评估了基于深度学习算法的气温订正方法相对数值预报性能的改进，并简要介绍了数据处理、训练模型、评估检验到实际应用的方法。检验结果表明：

(1) 从空间分布来看，DL模型预报的气温RMSE在大部分地区控制在2℃以下，其对ECMWF-IFS模式的订正效果明显，尤其是在湖南省西部和南部的雪峰山、武陵山、南岭地区有显著的改善，从海拔分布上看，改善率随着预报站点海拔的增加而上升，特别是海拔1200 m以上的站点，改善率达到50%左右。

(2) 模型预报的RMSE有明显的日变化，每日06时、09时，ECMWF-IFS误差最大(达2.7℃左右)，DL模型对其订正的幅度也最大(RMSE平均减小0.5℃)，二者在每日21时对应的时效误差最小，在不同海拔高度有不同的日变化特征。

(3) DL模型每个月相对ECMWF-IFS模式的平均RMSE都有明显的订正效果，二者在4月、5月(春季)误差最大，其中10月、11月(秋季)RMSE改善率最高(超过23%)，其次是3月、4月(春季，20%左右)，12月最低(9%)；DL订正产品在5月的平均RMSE>2℃，其他月份 < 2℃。

(4) 单次寒潮过程的检验效果表明，DL模型对ECMWF-IFS模式的系统误差有明显的订正效果：降温开始当天，日最低气温准确率提升30个百分点，第2天、第3天日最高气温准确率提升20个百分点，大部分时间的最低气温准确率也有明显的改善，在逐3 h预报上，RMSE平均减小0.2℃；在单站的曲线上，也能看出DL模型比ECMWF-IFS预报更接近观测实况。

湖南省气象台原有业务中使用的多模式最优集成，并没有针对数值模式带来误差的原因进行消除，其效果仅优于单个数值模式，但在一些地区(特别是山地)存在较明显的系统性误差，需要人工逐站订正。人工订正往往基于经验，一般参考前1~3 d数值预报的气温要素预报，假定短时期内预报偏差固定不变，并直接减去固定的偏差，这种方式无法定量考虑多要素对气温预报的影响，容易受到干扰和误导。

对比由他人发展的订正方法(如滑动双权重订正方法等)，本文中使用的方案更接近的是依据数值模式对当前天气形势场各要素的预报，来对不同下垫面不同地区的气温进行重新预报，而不是从原始预报值减去推导出的偏差值。在不同的地形，气温预报偏差受海拔、气压、云量、风场、湿度等因素影响，基于多气象因子的深度学习偏差订正更具有物理意义。

本文中采用的深度学习订正方法针对单站、单点建模，输出站点预报，在实际业务中设计出使用站点预报对背景预报场进行误差订正的方案，可以直接输出成各类服务产品，并作为第一优选客观预报源加入智能网格预报系统。在业务实践中，此产品逐3 h准确率评分高于其他所有参考预报来源、每日业务检验的高低温也高于其他来源。预报员大部分时间已不再进行手动订正(手动订正结果评分经常低于客观输出结果)，特别是在极端天气高发时期，节省了大量的时间和精力，体现了研究型业务成果在实际工作中发挥的巨大作用。

研究初期，统计了本地ECMWF-IFS、CMA-GFS全球预报以及华东、华南等区域模式的气温预报准确率及均方根误差，发现ECMWF-IFS综合误差最小，因此优先采用其进行建模训练。

因为时间关系，本文模型暂未就日最高/最低气温单独建模，仅使用拟合日变化曲线计算高/低温，未进行针对性评估(针对日最高/最低气温的预报模型也在研究、改进中)，基于我国高分辨率区域数值预报、CLDAS气温分析场的逐小时智能网格预报模型也在研究中，但因数据量较大，每次建模需要较长时间。但随着模型的逐步优化、算力的提升，后期将得到更加精准的预报结果。