强降雪天气形成的积雪是雪灾关键致灾因子之一(宫德吉和郝慕玲,1998; 时兴合等,2006)。2010年新年伊始,我国华北地区普降大到暴雪,降雪量达到历史同期第一位(李青春等,2011)。与此同时,1月3日20时北京南郊观象台观测的积雪深度达23.4 cm,突破历史极值。这场暴雪给人们的生产生活、尤其是交通出行等造成了非常严重的影响。2018年1月3—5日安徽省中北部出现了大暴雪到特大暴雪天气, 全省有51个市县积雪超过15 cm, 合肥积雪达到21 cm(杨祖祥等,2019)。受积雪影响,4日合肥市望江路公交站台顶板在大雪中倒塌, 造成一死多伤, 带来了极大的社会关注度。
雪水比,即某一时间段内(如24 h)降雪天气产生的新增积雪深度(单位:cm)与相应的降雪融化后形成的液态水量(单位:mm)之间的比值(国际上通常称为snow to liquid ratio或者snow ratio,简称SR),是降雪过程新增积雪深度预报所必须的重要参数(崔锦等,2017)。多年来,业务新增积雪深度预报多以经验预报为主,预报员根据新增积雪深度与降雪量之间的经验关系(雪水比经验值), 将降雪量预报换算成积雪深度预报。1878年加拿大的气象观测员根据多伦多安大略湖长期观测资料分析得到了当地平均雪水比为10∶1。此后,相当长的一段时间内,国内外气象业务部门利用雪水比10∶1对积雪深度进行简单的换算预报。然而,随着观测记录日益增多,分析发现雪水比10∶1是一个相当粗糙的近似值(Cobb and Waldstreicher, 2005)。Judson and Doesken(2000)对美国大量降雪过程进行了统计分析,表明雪水比为3∶1~100∶1。不少研究也表明不同降雪天气过程对应的雪水比数值相差甚远(Doesken and Juson, 1996; Super and Holroyd, 1997)。陈双和符娇兰(2021)对华北地区两次降雪过程的对比分析也表明不同天气过程雪水比差异非常大。由此可见,要开展新增积雪深度预报,就必须弄清楚我国降雪天气雪水比的气候分布特征。然而目前我国对雪水比气候特征的研究工作相对较少,起步较晚。杨琨和薛建军(2013)仅用了两个冬季的观测数据进行了研究,缺少不同季节不同区域雪水比的统计分析。近年来,崔锦等(2015)、王一颉等(2019)、杨成芳和朱晓晴(2020)、魏凌翔等(2021)对北方部分地区的雪水比气候特征及影响因子进行了分析,但缺乏全国范围内的分析。
曹冀鲁(2010)指出,我国气象业务部门仅发布降雪量预报,并不提供积雪深度预报产品,这容易造成公众对预报信息理解的偏差。为了满足日益增加的气象预报服务需求,有必要开展精细化积雪深度预报业务,然而,目前我国新增积雪深度预报技术支撑相对较薄弱。国际上积雪深度预报技术主要有四大类:数值模式预报、气候学、统计预报模型以及物理预报模型(Alcott and Steenburgh, 2010)。以欧洲中期天气预报中心全球预报模式(以下简称为ECMWF IFS)为例,其积雪深度预报是陆面物理过程的一部分,通过地表雪水含量和积雪密度计算得到积雪深度, 由于目前模式积雪密度采用一层模式,势必会导致密度偏大、积雪偏小(ECMWF,2020)。Roebber et al(2003;2007)通过分析温度、湿度、地面风场等物理因子与雪水比的统计关系,利用神经网络的方法建立了雪水比的统计预报模型。Cobb and Waldstreicher(2005)利用温度和雪水比的统计关系,以垂直速度作为权重系数建立了雪水比物理预报模型,并结合降雪量预报开发了新增积雪深度预报技术(以下简称Cobb算法),该技术已在美国气象部门得到了很好应用。考虑到利用统计模型需要大量的历史观测数据,2013年我国地面观测业务开始改革,夜间降水相态等人工观测业务取消,导致近年来降雪量等观测信息的缺失,因此本文主要参考Cobb算法构建新增积雪深度物理预报模型和客观预报技术。
本文利用地面站观测数据、ECMWF IFS模式预报数据、中央气象台智能网格降水、降水相态预报等资料对我国典型降雪过程的雪水比气候特征进行分析,在此基础上建立了新增积雪深度客观预报技术,并对其预报效果进行应用评估。
1 资料及方法介绍利用我国1951—2012年国家站地面观测数据集中的降雪量(SN)、风速、积雪深度数据,基于对典型降雪事件的定义选取了我国典型降雪个例,通过计算当日08时与前一日08时积雪量差,获得当日08时24 h累计新增积雪量(NSD),利用式(1)得到雪水比(SR),并对其进行气候统计。此外,利用ECMWF-IFS模式预报的温度、相对湿度和垂直速度等物理量(空间分辨率为0.2°,时间分辨率为3 h和6 h)、中央气象台智能网格降水和相态预报产品(空间分辨率为5 km,时间分辨率为3 h) 以及5 km分辨率地形数据建立了雪水比和新增积雪深度客观预报技术。进一步利用2019年10月至2020年3月地面积雪观测、ECMWF-IFS模式积雪深度预报及新增积雪深度客观预报数据,通过计算式(2)的TS评分对新增积雪深度客观预报产品预报性能进行评估。
| $ S R=\frac{N S D}{S N} $ | (1) |
| $ T S=\frac{N_a}{N_a+N_b+N_c} $ | (2) |
式中: Na为预报正确站点数,Nb为空报站点数,Nc为漏报站点数。
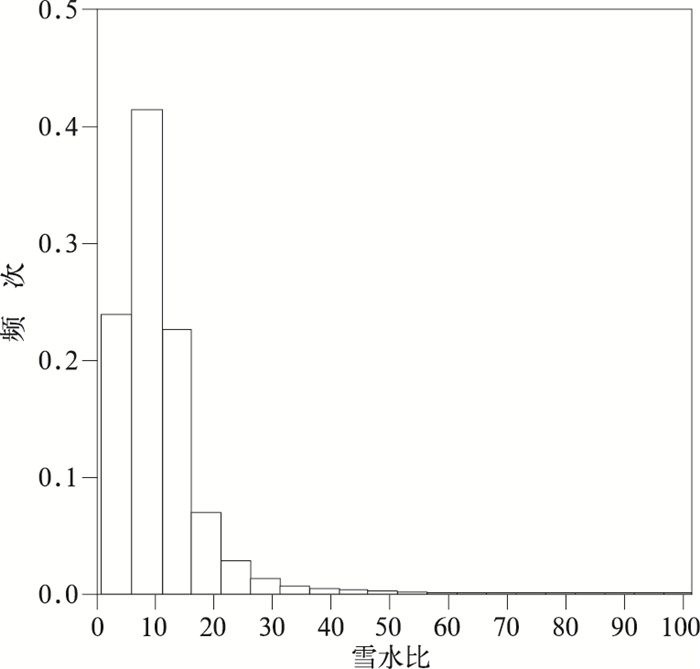
2 我国典型降雪天气雪水比气候特征分布为避免弱降雪观测不精确以及风吹雪等对积雪的影响(Roebber et al, 2003),典型降雪个例选取标准为:24 h累计降雪量≥2.5 mm,累计新增积雪深度≥3 cm,同时地面风速 < 9 m·s-1。需要说明是,尽管对降雪个例进行了筛选,但是我国积雪观测资料只有08时24 h累计积雪量记录,中间可能出现融雪等现象,因此可能会导致计算的雪水比比实际值要偏小。通过对我国1951—2012年国家站降水量、积雪深度以及10 m风场等观测数据进行筛选,共有800个站点44 567个站次满足上述标准。根据式(1)雪水比的计算方法,利用24 h累计降雪量和新增积雪深度观测数据,计算得到所有站次的雪水比,并对所有站次以及558个站点(该站点样本数大于10)雪水比进行了时空特征分析。从所有站次雪水比统计特征分布可以看出(图 1),雪水比分布非常广,最小值为0.3∶1,最大值为100∶1,仅有1705个站次雪水比为10∶1(9.5∶1~10.4∶1),占比4%左右,与Roebber et al(2013)的研究结果基本一致。按照基于雪水比的降雪性质分类方法,可将降雪分为干雪个例(SR≥15∶1)、湿雪(SR≤9∶1) 以及正常降雪(9∶1 < SR < 15∶1)(Roebber et al, 2003)。按照上述分类,所选个例干雪约占17%,湿雪占比约53%,正常降雪约占30%。
|
图 1 我国44 567个站次雪水比频次统计分布 (x坐标数值为比值,如10代表 10∶1) Fig. 1 Frequency distribution of snow to liquid ratios for 44 567 samples over China (The numbers at x axis are ratios, for example, 10 means 10∶1) |
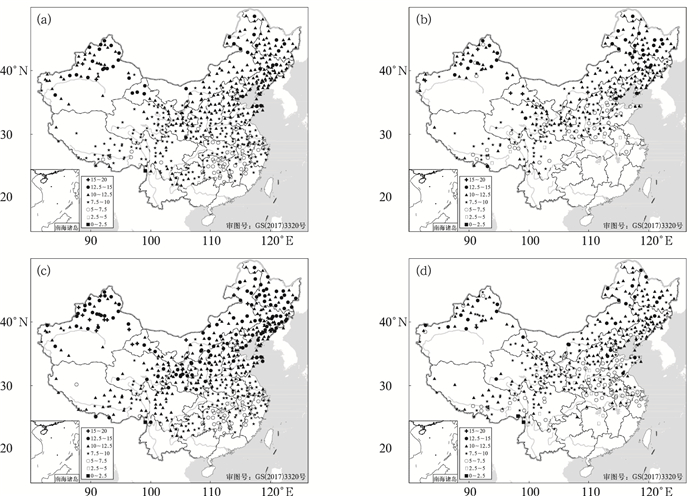
杨琨和薛建军(2013)分析指出雪水比具有明显的地区差异。为此,进一步对雪水比时空分布进行分析。图 2a为冬半年雪水比平均值的空间分布,新疆、西北地区东部、华北、东北地区等地雪水比气候均值≥10∶1,其中内蒙古东北部、黑龙江及新疆、甘肃西部等地的部分地区雪水比平均值>12∶1,最大可达16∶1;青藏高原地区、黄淮、江淮、江汉以及贵州等地雪水比均值为 < 10∶1、>7∶1, 江南等地大部地区雪水比 < 7∶1,云南西北部个别站点雪水比 < 5∶1。与此同时,从春、秋季以及冬季雪水比平均值分布可以看出(图 2b~2d), 雪水比表现出一定的季节差异,总体而言冬季雪水比最大,其次为春季,秋季最小;冬季,黄淮及其以北大部地区平均雪水比>10∶1;秋季仅新疆、甘肃中西部、内蒙古中东部以及东北地区大部雪水比>10∶1;此外,华北、黄淮、江淮、江汉以及青藏高原东部等地雪水比季节特征最显著。Roebber et al(2007)研究指出,雪水比受大气温度、湿度、地面和地表温度等因素影响。由于我国不同季节、不同区域大气温度、湿度以及地面和地表温度等气象条件存在较大的差异,我国雪水比存在明显的季节性以及区域性特征。基于气候学或者经验值的雪水比对新增积雪深度进行预报将会带来较大的预报偏差。
|
图 2 我国(a)冬半年、(b)秋季、(c)冬季、(d)春季典型降雪天气雪水比气候特征分布 (图例数值实际为比值,如15~20代表 15∶1~20∶1) Fig. 2 Climatological distribution of snow to liquid ratio in typical snowfall events in (a) winter half year, (b) autumn, (c) winter, and (d) spring (The numbers in the legends are ratios, for example, 15-20 means 15∶1-20∶1) |
积雪形成与云内、云外以及地面过程等有关(Roebber et al, 2003),其中云内微物理过程对积雪形成至关重要。Cobb算法建立的雪水比及积雪深度物理预报模型主要考虑了云内微物理过程对积雪深度的影响。研究表明:云内-18~-12℃温度层最有利于树枝状冰晶的形成,对应的降雪雪密度低,雪水比大,高于或低于该温度则雪密度增加,雪水比明显减小(Libbrecht, 2006)。在饱和情况下,垂直速度与单位时间降水率直接有关,大的垂直速度将会把云内过冷却水带到更高的冰晶层内,从而有利于冰晶增长,并进一步影响雪水比,因此基于Cobb算法构建的预报模型重点引入了云内温度、垂直速度等变量计算雪水比(Cobb and Waldstreicher, 2005)。本文参考Cobb算法利用ECMWF IFS模式输出的高空温度、相对湿度、垂直速度以及高度场等变量建立了雪水比预报模型,算法具体如下:
首先需要在模式输出的湿度廓线内识别出云,Cobb算法(Barnwell, 2011)利用相对湿度>90%来识别云,根据中央气象台多年预报经验表明,模式预报的相对湿度达到85%左右就有可能出现降雪,因此本文将云定义为相对湿度≥85%。考虑到地形的影响,不同海拔高度云识别的上下边界选择的气压层不一样,云识别范围的下边界气压层位势高度必须≥地形高度(H),上边界最高气压层选取标准如下:
当H≥4000 m,最高气压层为100 hPa;
当2000 m≤H < 4000 m,最高气压层为200 hPa;
当1000 m≤H < 2000 m,最高气压层为300 hPa;
当H < 1000 m,最高气压层为400 hPa。
其次,计算云内各层雪水比权重系数Wi,具体如下:
| $ W_i=\omega\left(\frac{\omega}{\omega_{\max }}\right)^2\left(\phi_2-\phi_1\right) $ | (3) |
式中:ωmax为整个云体内最大垂直上升速度,ω是任意云层内的平均垂直上升速度,ϕ2、ϕ1为云层上下边界的位势高度。
SRi(T)为云内某一气压层上的雪水比,由雪水比和温度的统计关系得到。最后,计算整个云内加权的雪水比WSRi,并将各层雪水比累加得到最终雪水比WSR,具体如下:
| $ W S R_i=S R_i(T) \times \frac{W_i}{\sum W_i} $ | (4) |
| $ W S R=\sum W S R_i $ | (5) |
由于ECMWF IFS模式空间分辨率为9 km,为了得到更精细的积雪深度预报产品,利用双线性插值方法将模式温度、相对湿度、垂直速度以及高度场插值到5 km分辨率。结合5 km分辨率地形数据以及上述变量,根据式(3)~式(5)分析得到5 km分辨率的雪水比预报产品。
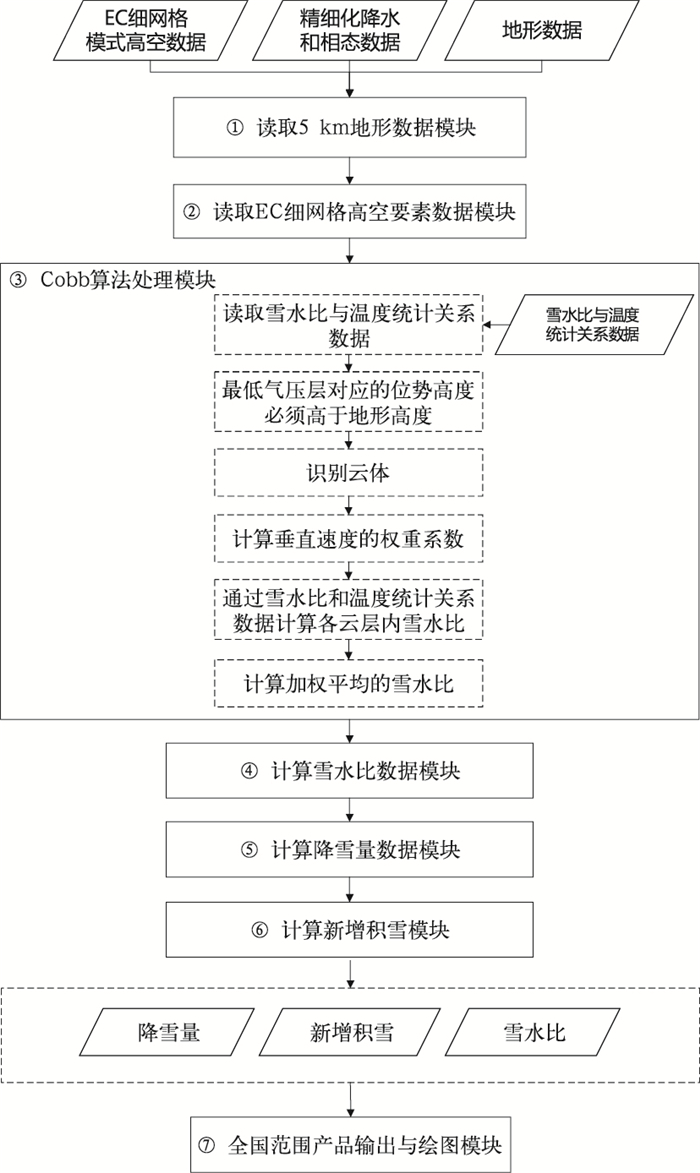
在雪水比预报模型的基础上,根据雪水比计算式(1),用雪水比乘以降雪量即可得到新增积雪深度。由于数值模式降水量(曹勇等,2016)和相态预报(董全等,2020a;2020b)存在一定的预报偏差,预报的精细化程度也无法满足业务预报需求。近年来,中央气象台发展了智能网格降水量和相态预报技术。从预报效果来看,格点化定量降水预报TS评分和均方根误差均较ECMWF IFS模式降水预报有一定提高(曹勇等,2016)。基于集合预报系统的最优概率阈值法构建的相态预报技术较集合预报系统控制成员及ECMWF IFS模式预报显著提高了降水相态预报能力(董全等,2020a;2020b)。因此, 本文降雪量预报数据来源于中央气象台智能网格降水以及相态预报产品,通过判断逐3 h或6 h的降水相态类型,将出现降雪时段的降水量确定为相应时段的降雪量,结合雪水比预报模型即可得到相应时段的新增积雪深度预报,具体技术流程见图 3。根据上述技术流程,发展了雪水比、新增积雪深度预报技术,相应的产品空间分辨率为5 km,1~3 d预报时效时间分辨率为3 h、6 h、24 h,4~10 d预报时效时间分辨率为6 h、24 h。
|
图 3 新增积雪预报技术流程框架图 Fig. 3 Flow chart of fresh snowfall depth forecast technology |
考虑到地形的影响,不同于Cobb算法预报模型(以下简称Cobb方案)对云识别范围定义(云识别范围为1000~500 hPa)(Cobb and Waldstreicher, 2005),本文所采用的算法(以下简称为改进后的Cobb方案)在云识别方案中对不同地形高度区域的云识别范围进行了规定,具体见上文。为了对比不同云识别方案对新增积雪预报性能的影响,本文选取典型个例进行分析。2018年1月3日,西北地区东部、华北西部、黄淮西部、江淮、江汉等地出现了大范围强降雪,大部地区出现了中到大雪,陕西关中平原、山西南部、河南西部和南部、安徽中北部、湖北中北部等地出现暴雪到大暴雪,局地特大暴雪(图 4a)。需要说明的是,考虑到有些区域出现了雨雪相态转化,由于积雪只有24 h累计量观测,为了保证分析的准确性,分析时已将24 h内出现了雨雪相态转化的站点过滤掉。受其影响,上述大部地区新增积雪深度达到3~10 cm,其中,陕西关中平原、山西南部、河南西部和南部、湖北北部、安徽中北部等地的部分地区新增积雪深度高达10~30 cm,局地超过30 cm(图 5a)。通过积雪深度观测及降雪量计算得到实况24 h雪水比(图 6a),实况雪水比表现出明显的区域差异,河南中南部、湖北中北部、苏皖北部等地雪水比为3∶1~10∶1,局地大于10∶1,而西北地区东部、山西中南部、河南北部等地大部分地区雪水比在10∶1~25∶1,局地大于30∶1。

|
图 4 (a) 2018年1月4日08时观测的降雪量(彩色点,单位:mm)及(b)中央气象台智能网格36 h预报时效降雪量预报(填色) Fig. 4 (a) The observed snowfall at 08:00 BT 4 January 2018 (colored dots, unit: mm) and (b) the forecasted snowfall (colored) with 36 h lead time using different cloud identify strategies |
|
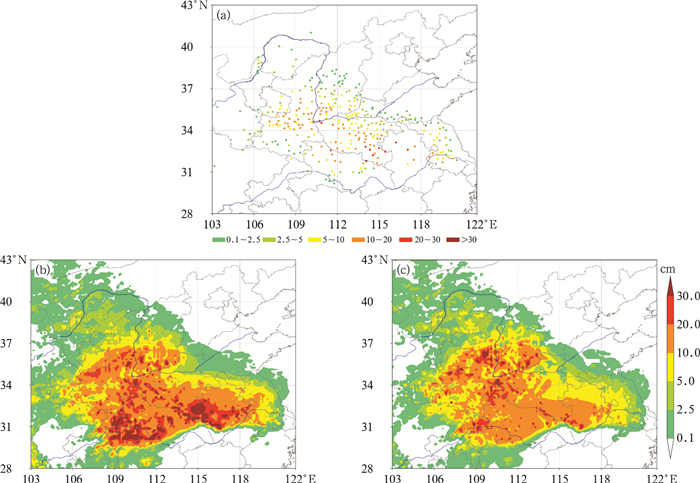
图 5 (a) 2018年1月4日08时观测的24 h累计新增积雪深度(单位:cm)及(b)改进后的Cobb方案, (c)Cobb方案36 h时效24 h累计新增积雪预报(填色) Fig. 5 (a) The observed 24 h accumulated fresh snowfall depth (unit: cm) at 08:00 BT 4 January 2018 and (b, c) the forecasted 24 h accumulated fresh snowfall depth (colored) with 36 h lead time by (b) modified Cobb method and (c) Cobb method |

|
图 6 (a) 2018年1月4日08时观测的24 h累计雪水比实况以及(b)改进后的Cobb方案, (c)Cobb方案的雪水比预报 (图例数值为比值,如15.0代表 15.0∶1;蓝色方框为图 8时间-高度剖面分析所在位置) Fig. 6 (a) The observed 24 h accumulated snow to liquid ratio at 08:00 BT 4 January 2018 and (b, c) forecasted 24 h accumulated snow to liquid ratio at 36 h lead time by (b) modified Cobb method and (c) Cobb method (The numbers in the legends are ratios, for example, 15.0 means 15.0∶1; The blue rectangle is used by the cross section analysis of Fig. 8) |
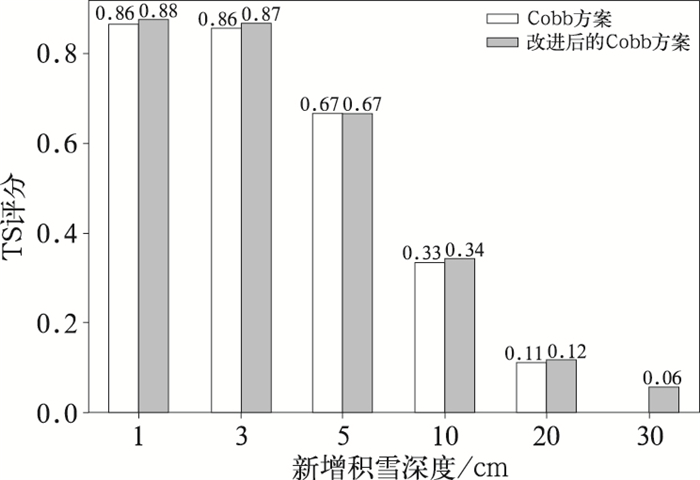
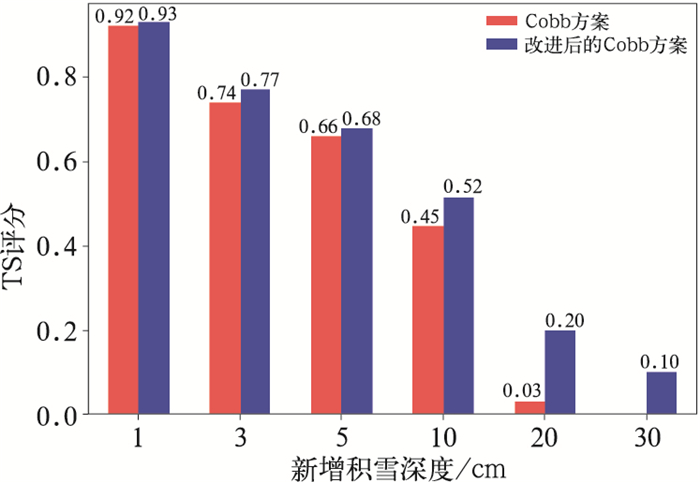
图 4b显示,对于上述地区的降雪,中央气象台智能网格预报的降雪范围和强度与实况基本一致,仅在湖北西南部等地降雪预报较实况偏大。湖北西南部降雪偏大的主要原因是智能网格相态预报为纯雪,而实况该地区为降雨。对比改进后的Cobb方案与Cobb方案相应的新增积雪预报可见(图 5b, 5c),除了在湖北西南部因相态预报偏差出现明显空报之外,二者预报的新增积雪与实况基本一致,但改进后的Cobb方案对河南东南部、安徽北部以及湖北北部大于20cm新增积雪深度预报更接近实况,且在河南等地预报出了30 cm以上的积雪,与实况相符。Cobb方案对上述地区的新增积雪深度明显偏小,对山西中部、河南东北部等地新增积雪深度高估。从TS评分也可以看出(图 7),改进后的Cobb方案各量级新增积雪深度均较Cobb方案的TS评分提高明显,尤其对大于10 cm及以上量级的预报TS评分提高率大于18%。
|
图 7 2018年1月4日08时36 h时效基于改进后的Cobb方案和Cobb方案新增积雪深度预报TS评分 Fig. 7 TS scores of fresh snowfall depth forecast with 36 h lead time at 08:00 BT 4 January 2018 based on different cloud identification strategies |
对比分析Cobb方案与改进后的Cobb方案雪水比预报可以发现(图 6b, 6c),两个方案预报的雪水比空间分布与实况较为一致,但Cobb方案对山西、河南北部雪水比预报明显较实况偏大,对于河南南部等地雪水比预报略偏小,而改进后的Cobb方案对河南、山西等地的预报更接近实况,较为准确地预报了河南东南部20 cm以上新增积雪,并减少了山西中部和河南北部积雪深度高估情况。
可见,两个方案新增积雪深度以及雪水比预报差异最大主要位于河南东南部等地。为进一步说明二者偏差来源,以河南东南部为例,对其温度、湿度以及垂直速度的垂直结构进行分析。从ECMWF IFS模式2日20时预报的物理量廓线可以看出(图 8),最有利于冰晶增长的温度层结(-18~-12℃)位于500~400 hPa,且最大垂直速度基本与该层结重合,根据陈双和符娇兰(2021)、Libbrecht(2006)等研究表明,1 000~400 hPa层内温度和垂直速度的垂直分布更有利于密度较小、雪水比大、积雪深度大的降雪产生,Cobb方案仅考虑1000~500 hPa层内的温度和抬升速度对雪水比的影响,由于该层结内温度普遍高于-12℃,过冷却水含量较高,更有利于密度大、雪水比小的降雪产生,这也就是改进后的Cobb方案雪水比较Cobb方案大、预报的新增积雪深度与实况更为接近的原因。

|
图 8 ECMWF IFS模式2018年1月2日20时预报的2日20时至4日20时区域(32.3°~33.3°N、114.3°~115.8°E)平均温度(红色线及填色, 单位:℃)、相对湿度(绿色实线, 单位:%)及垂直速度(黑色线, 单位:Pa·s-1)时间-高度剖面对比 Fig. 8 The forecast profile averaged over area (32.3°-33.3°N, 114.3°-115.8°E) of temperature (red solid lines and colored, unit: ℃), relative humidity (green solid lines, unit: %) and vertical velocity (black lines, unit: Pa·s-1) by ECMWF IFS model at 20:00 BT 2 for the period of 20:00 BT 2 to 20:00 BT 4 January 2018 |
2019年11月17日,吉林大部、黑龙江等地普降大到暴雪,吉林东部、黑龙江东部出现大暴雪,局地特大暴雪,大部地区降雪量预报与实况基本一致,黑龙江中西部略偏大(图略)。图 9显示,吉林大部、黑龙江大部24 h新增积雪深度超过5 cm,吉林大部、黑龙江东部新增积雪深度10 cm以上,局地达到30 cm。总体而言,两个方案新增积雪深度预报对吉林中东部和黑龙江东部积雪深度预报与实况基本一致,基于改进后的Cobb算法准确预报了吉林东部局地30 cm积雪,但二者对30 cm积雪范围预报较实况偏大。此外,对黑龙江中西部积雪预报也略偏大;一部分是由于降雪量预报较实况略偏大(图略),另一部分原因则与雪水比预报偏差有关。进一步对比两种方案的雪水比预报发现(图 10),基于Cobb算法的雪水比较实况明显偏大,尤其是在黑龙江中西部,基于改进后的Cobb算法对雪水比偏大的误差有明显改进。从图 10a蓝色方框内的温度、湿度及垂直速度剖面可以看出(图略),降水期间,云层伸展高度达到了400 hPa及以上,最有利于冰晶增长的温度层结位于925~700 hPa,最大抬升速度主要位于500 hPa及以下,同时,黑龙江中西部地形复杂,大部分地区地形高度在500 m以上,因此基于改进后的Cobb算法较基于Cobb算法的雪水比小,且更接近实况。从新增积雪深度预报TS评分可以看出(图 11),基于改进后的Cobb算法新增积雪深度预报TS高于基于Cobb算法的新增积雪深度预报。
综上所示,基于改进后的Cobb方案相对Cobb方案对雪水比及新增积雪预报改进明显。需要指出的是,Cobb方案及改进后的Cobb方案仅考虑了与云内微物理过程有关的温湿廓线对新增积雪深度的影响,并未考虑融雪等近地面过程。由于目前常规积雪深度观测仅有24 h累计量,期间发生的融雪量无法观测。因此,本文所探讨的雪水比有可能比实际雪水比大,这可能是上述个例中本方案预报的雪水比在部分地区较实况雪水比偏大的可能原因。目前,即使是预报性能最好的ECMWF IFS模式,也不能较好地把降雪伴随的地面融化过程刻画好,未来还需要增加地面融雪预报技术的研发。
4 新增积雪客观预报产品检验评估为更好评估新增积雪客观预报产品预报性能,利用全国国家站08时实况积雪深度观测资料对2019年10月至2020年3月期间新增积雪客观预报产品以及ECMWF IFS模式新增积雪预报产品的预报情况进行了检验。用当日08时积雪深度观测量减去前一日08时积雪深度观测量得到当日08时24 h累计新增积雪深度实况资料。ECMWF IFS模式积雪预报(sd)数据是通过积雪当量预报(SWE)以及雪密度D计算得到,具体见式(6)。进一步参考实况新增积雪深度计算方法得到ECMWF IFS模式新增积雪深度预报数据。
| $ s d=\frac{S W E \times 10^5}{D} $ | (6) |
式中:D为降雪密度(单位:kg·m-3),SWE为积雪深度当量(单位:10-7 m·kg·m-3),sd为积雪深度(单位,cm)。
利用双线性插值方法将ECMWF IFS模式和基于改进后的Cobb算法新增积雪预报数据插值到实况新增积雪站点上,并计算新增积雪TS评分。参照降雪量等级及积雪观测业务规范,评分等级分别为1、3、5、10、20、30 cm,并进一步按照下式计算了相对ECMWF IFS模式新增积雪预报产品的TS评分提高率(RIT)。
| $ R I T=\frac{T_{\mathrm{sa}}-T_{\mathrm{sb}}}{T_{\mathrm{sb}}} \times 100 \% $ | (7) |
式中:Tsa为基于改进后的Cobb算法新增积雪预报产品TS评分,而Tsb为ECMWF IFS模式新增积雪预报产品的TS评分。
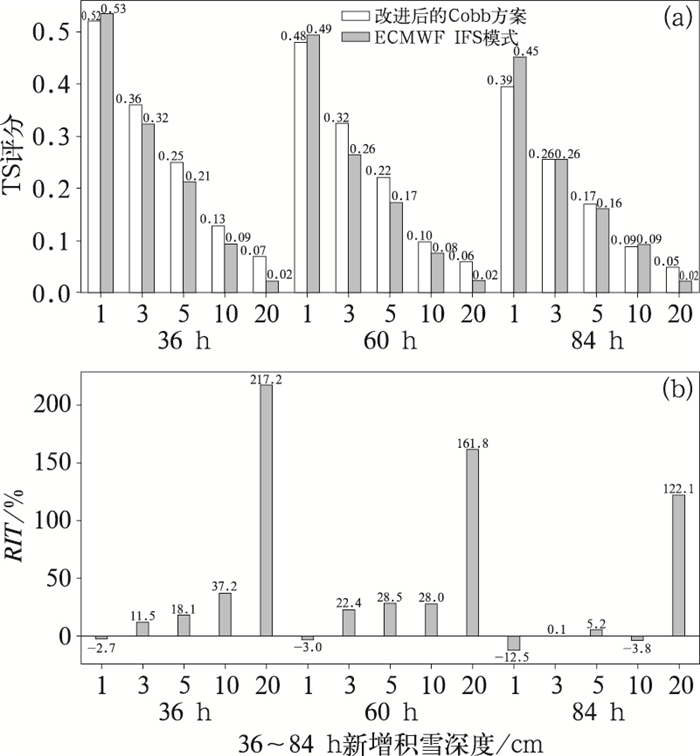
从提前1~3 d的预报评分可以看出(图 12),基于改进后的Cobb算法新增积雪深度预报产品对绝大部分量级新增积雪深度预报评分要优于ECMWF IFS模式,提前2 d预报评分提高率基本达到了10%以上(图 12a),尤其是大于20 cm新增积雪深度预报,评分相对模式提高率超过100%(图 12b),可见,该方法相对数值模式改进明显。对于30 cm以上新增积雪深度预报评分,提前1~2 d该方法较模式略有降低。通过分析发现,2019年10月1日至2020年3月20日期间,30 cm以上新增积雪观测记录主要位于西藏边境线附近,考虑到该地区观测极少,模式预报的降雪强度通常较观测强,易造成空报,中央气象台智能网格降水预报对此处降雪量进行了一定程度的消空,可能造成对个别强降雪过程的漏报,从而导致新增积雪深度预报偏小。
|
图 12 2019年10月1日至2020年3月20日短期时效(36~84 h)(a)基于改进后的Cobb算法和ECMWF IFS模式新增积雪深度预报TS评分,(b)改进后的Cobb算法相对于ECMWF IFS模式预报TS评分提高率 Fig. 12 (a) TS scores of fresh snowfall depth forecast with 36-84 h lead time during the period from 1 October 2019 to 20 March 2020 and (b) the increase rate of modified Cobb method forecast relative to that by the ECMWF IFS model |
本文利用历史观测数据对我国典型降雪过程的雪水比气候特征进行了统计研究,在此基础上,构建了基于改进后的Cobb算法的雪水比及新增积雪深度客观预报技术,并对其进行了应用评估,具体结论如下:
(1) 我国典型降雪过程的雪水比统计分布较广,最小值为0.3∶1,最大值为100∶1,仅有4%左右的雪水比为10∶1,雪水比位于9∶1~15∶1的样本占比也仅有30%左右。雪水比具有明显的季节和区域特征,北方地区雪水比较南方地区大,冬季雪水比较秋、春季大。
(2) 基于改进后的Cobb方案建立了雪水比及新增积雪预报技术。较原Cobb方案,改进后的Cobb方案考虑了地形对不同区域降雪云边界识别及云内温度及垂直抬升速度廓线的影响,检验表明改进后的Cobb方案雪水比和新增积雪预报性能较原方案改进明显。
(3) 基于改进后的Cobb算法新增积雪预报性能较好,准确率较ECMWF IFS模式预报有明显提高,短期时效内(1~3 d)大部分量级预报提高率均在10%以上,尤其是对于20 cm以上的新增积雪深度,提高率可达100%及以上。
本文利用改进后的Cobb算法构建了雪水比和新增积雪预报技术,该技术已在中央气象台得到很好应用,并加入了“智慧冬奥2022天气预报示范计划”,为冬季强降雪预报以及2022年北京冬奥会赛事气象服务保障提供了有力的技术支撑。应用评估表明,尽管该预报技术较模式积雪预报有明显提升,但仍有较大的改进空间,一方面降水相态预报难度较大,当出现较复杂的相态转换过程,降水相态预报可能会出现一定的误差,进而会导致新增积雪预报出现较大偏差;此外,降雪过程近地面温度或地表温度高于0℃,就会出现一定的融雪现象,而目前研发的新增积雪预报技术并未考虑到地面融雪过程,这也会影响到新增积雪预报准确率(胡宁等,2021;杨成芳和刘畅,2019)。因此,未来需要进一步提升降水相态预报性能,同时,探索近地面融雪过程对新增积雪深度的影响及相应的预报技术,从而更好地提高新增积雪预报准确率。
曹冀鲁, 2010. 降雪量和积雪深度一样吗[J]. 气象知识, (1): 28. Cao J L, 2010. Is the amount of snowfall the same as the depth of snow?[J]. Meteor Knowl, (1): 28 (in Chinese).
|
曹勇, 刘凑华, 宗志平, 等, 2016. 国家级格点化定量降水预报系统[J]. 气象, 42(12): 1476-1482. Cao Y, Liu C H, Zong Z P, et al, 2016. State level gridded quantitative precipitation forecasting system[J]. Meteor Mon, 42(12): 1476-1482 (in Chinese).
|
陈双, 符娇兰, 2021. 华北地区雪密度不同的两次降雪过程对比分析[J]. 气象, 47(1): 36-48. Chen S, Fu J L, 2021. Comparative analysis of two snow events with different snow density in North China[J]. Meteor Mon, 47(1): 36-48 (in Chinese).
|
崔锦, 周晓珊, 阎琦, 等, 2015. 沈阳降雪含水比变化特征及其大气影响因子[J]. 冰川冻土, 37(6): 1508-1514. Cui J, Zhou X S, Yan Q, et al, 2015. Snow-to-liquid ratio variation and its atmospheric influence factors in Shenyang[J]. J Glaciol Geocryol, 37(6): 1508-1514 (in Chinese).
|
崔锦, 周晓珊, 阎琦, 等, 2017. 降雪含水比研究进展[J]. 气象, 43(6): 735-744. Cui J, Zhou X S, Yan Q, et al, 2017. Advances in snow-to-liquid ratio[J]. Meteor Mon, 43(6): 735-744 (in Chinese).
|
董全, 胡宁, 宗志平, 2020a. ECMWF降水相态预报产品(PTYPE)应用和检验[J]. 气象, 46(9): 1210-1221. Dong Q, Hu N, Zong Z P, 2020a. Application and verification of the ECMWF precipitation type forecast product (PTYPE)[J]. Meteor Mon, 46(9): 1210-1221 (in Chinese).
|
董全, 张峰, 宗志平, 2020b. 基于ECMWF集合预报产品的降水相态客观预报方法[J]. 应用气象学报, 31(5): 527-542. Dong Q, Zhang F, Zong Z P, 2020b. Objective precipitation type forecast based on ECMWF ensemble prediction product[J]. J Appl Meteor Sci, 31(5): 527-542 (in Chinese).
|
宫德吉, 郝慕玲, 1998. 白灾成灾综合指数的研究[J]. 应用气象学报, 9(1): 119-123. Gong D J, Hao M L, 1998. Synthetical indexes of the disaster of snow cover[J]. Quart J Appl Meteor, 9(1): 119-123 (in Chinese).
|
胡宁, 符娇兰, 孙军, 等, 2021. 北京一次冬季极端降水过程中相态转换预报的误差分析[J]. 气象学报, 79(2): 328-339. Hu N, Fu J L, Sun J, et al, 2021. Errors in the forecast of precipitation type transition in an extreme winter precipitation event in Beijing[J]. Acta Meteor Sin, 79(2): 328-339 (in Chinese).
|
李青春, 程丛兰, 高华, 等, 2011. 北京一次冬季回流暴雪天气过程的数值分析[J]. 气象, 37(11): 1380-1388. Li Q C, Cheng C L, Gao H, et al, 2011. Numerical simulation and analysis on a heavy snow of return-flow events in Beijing[J]. Meteor Mon, 37(11): 1380-1388 (in Chinese).
|
时兴合, 李凤霞, 扎西才让, 等, 2006. 1961—2004年青海积雪及雪灾变化[J]. 应用气象学报, 17(3): 376-382. Shi X H, Li F X, Zhaxi C R, et al, 2006. The variation of snow-cover and snow disaster in Qinghai during 1961-2004[J]. J Appl Meteor Sci, 17(3): 376-382 (in Chinese).
|
王一颉, 赵桂香, 马严枝, 2019. 降水相态转换机制及积雪深度预报技术研究[J]. 干旱气象, 37(6): 964-971. Wang Y J, Zhao G X, Ma Y Z, 2019. Precipitation phase transformation mechanism and prediction technology of snow depth[J]. J Arid Meteor, 37(6): 964-971 (in Chinese).
|
魏凌翔, 童金, 邱学兴, 2021. 安徽省积雪效率和积雪密度特征分析[J]. 气象与环境科学, 44(3): 24-30. Wei L X, Tong J, Qiu X X, 2021. Characteristic analysis of snow cover efficiency and snow density in Anhui Province[J]. Meteor Environ Sci, 44(3): 24-30 (in Chinese).
|
杨成芳, 刘畅, 2019. 一次江淮气旋暴雪的积雪特征及气象影响因子分析[J]. 气象, 45(2): 191-202. Yang C F, Liu C, 2019. Study on snow cover and its meteorological influence factors of Jianghuai cyclone snowstorm[J]. Meteor Mon, 45(2): 191-202 (in Chinese).
|
杨成芳, 朱晓清, 2020. 山东降雪含水比统计特征分析[J]. 海洋气象学报, 40(1): 47-56. Yang C F, Zhu X Q, 2020. Analysis on statistical characteristics of snow-to-liquid ratio in Shandong[J]. J Mar Meteor, 40(1): 47-56 (in Chinese).
|
杨琨, 薛建军, 2013. 使用加密降雪资料分析降雪量和积雪深度关系[J]. 应用气象学报, 24(3): 349-355. Yang K, Xue J J, 2013. The relationship between snowfall and snow depth using intensive snowfall observations[J]. J Appl Meteor Sci, 24(3): 349-355 (in Chinese).
|
杨祖祥, 谢亦峰, 项阳, 等, 2019. 2018年1月初安徽特大暴雪的双偏振雷达观测分析[J]. 暴雨灾害, 38(1): 31-40. Yang Z X, Xie Y F, Xiang Y, et al, 2019. Analysis on dual polarization radar observations of a heavy snowstorm event in Anhui in the beginning of January 2018[J]. Torr Rain Dis, 38(1): 31-40 (in Chinese).
|
Alcott T I, Steenburgh W J, 2010. Snow-to-liquid ratio variability and prediction at a high-elevation site in Utah's Wasatch Mountains[J]. Wea Forecasting, 25(1): 323-337.
|
Barnwell J, 2011. Verification of the cobb snowfall forecasting algorithm[D]. Lincoln: University of Nebraska-Lincoln.
|
Cobb D K Jr, Waldstreicher J S, 2005. A simple physically based snowfall algorithm[C]//Preprints, 21st Conf. on Weather Analysis and Forecasting and 17th Conf. on Numerical Weather Prediction. Washington, DC: American Meteorological Society.
|
Doesken N J, Judson A, 1996. The Snow Booklet: A Guide to the Science, Climatology, and Measurement of Snow in the United States[M]. Fort Collins, Colorado, USA: Colorado State University: 1-86.
|
ECMWF, 2020. IFS Documentation - Cy47r1 Operational implementation 30 June 2020. Part Ⅳ: physical processes[R]. Reading, England: ECMWF: 137-146.
|
Judson A, Doesken N, 2000. Density of freshly fallen snow in the central rocky mountains[J]. Bull Amer Meteor Soc, 81(7): 1577-1588.
|
Libbrecht K G, 2006. Ken Libbrecht's Field Guide to Snowflakes[M].
Minnesota: Voyageur Press: 1-112.
|
Roebber P J, Bruening S L, Schultz D M, et al, 2003. Improving snowfall forecasting by diagnosing snow density[J]. Wea Forecasting, 18(2): 264-287.
|
Roebber P J, Butt M R, Reinke S J, et al, 2007. Real-time forecasting of snowfall using a neural network[J]. Wea Forecasting, 22(3): 676-684.
|
Super A B, Holroyd E W III, 1997. Snow accumulation algorithm for the WSR-88D radar: Second annual report[R]. Denver, CO: U.S. Dept of Interior Tech Rep: 1-77.
|
 2022, Vol. 48
2022, Vol. 48