引言

由于模式本身的不足，包括降水在内的许多要素预报都存在着系统性的预报偏差，但与其他大多数要素不同，一方面, 降水在时间上不连续，空间上有较强的尺度依赖性；另一方面，降水的概率密度函数是典型的偏态分布，使得确定模式降水预报偏差相对其他要素更加困难(毕宝贵等，2016；洪伟和郑玉兰，2018；唐文苑和郑永光，2019；符娇兰和代刊，2016；赵瑞霞等，2020；潘留杰等，2016)。

气象工作者发展了一系列后处理技术来量化降水预报中的不确定性和减少预报的系统性偏差(Hamill et al，2008；Bentzien and Friederichs, 2012；吴晶等，2020)。典型的后处理方法主要有：集合预报统计量(Roulston and Smith, 2003；Wang and Bishop, 2005)、贝叶斯模型平均(Raftery et al，2005；Sloughter et al，2007)、地理位置平均(Kleiber et al，2011)，非齐次高斯回归(Gneiting and Raftery, 2005)、逻辑回归(Hamill and Whitaker, 2006)、扩展逻辑回归(Wilks，2000)。其他的工作还包括：Yuan et al(2007)应用人工神经网络作为后处理器对NCEP区域谱模式集合预报系统的降水预报进行校正；Voisin et al(2010)应用了两种空间分解偏差校正方法和降尺度误差校准模拟技术来改进集合预报系统的降水表现；Atger(2003)将简单的线性回归应用到站点降水预报订正上；Hamill and Whitaker(2006)则采用预报降水量与实际观测降水量的分位数映射关系来提高降水的预报准确率。这些后处理方法在某些方面或者某种程度上提高了模式降水的预报表现，但具体选用哪种方法不仅取决于模式在当地的预报特点和表现，而且还取决于实际的预报目标。

近年来发展的频率匹配是模式降水预报后处理订正中最为有效的方法之一。本质上来说，频率匹配是通过调整降水预报值，使其在特定的阈值范围内的降水预报频率与观测频率保持一致来实现的。频率匹配的作用是使模式的预报偏差Bias接近于1，实际计算上也包括偏差调整(Mesinger，2008)和偏差去除(Clark et al，2009)两种技术。国内已有的工作中，李莉等(2011)采用频率匹配的方法对T213降水预报进行了订正，结果表明该方法对其降水预报偏差有明显改善；李俊等(2014)针对中尺度暴雨数值预报模式(AREM)降水预报的偏差特征，开展了基于频率(或面积)匹配方法的降水偏差订正试验。但总体来说，频率匹配方法的研究工作并不深入，特别是针对近年来在高分辨率模式基础上迅速发展的精细化网格降水预报业务方面的应用就更为少见。本文基于ECMWF模式降水预报、自动气象站降水观测资料以及网格降水量融合分析产品，研究卡尔曼动态频率匹配订正方法在高分辨率网格降水预报中的预报表现，进而将其应用于实际预报业务，以提高网格降水的精细化预报能力。

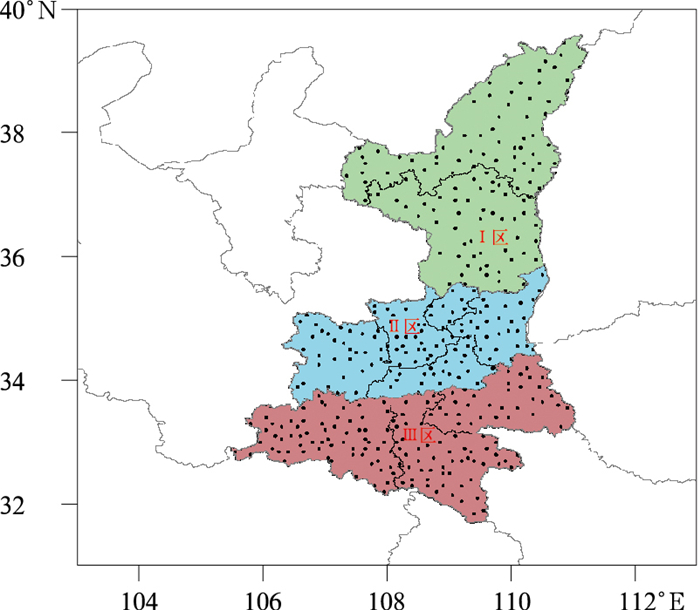
1 数据资料

选取388个观测站点24 h逐日累计降水观测资料，388个站点(图 1)包括98个县级观测站和290个无人自动气象站。资料经过严格的质量控制，具有较高的观测质量，时段为2019年1月1日至2020年2月29日。此外，在降水个例对比检验中，为了更加清楚地分析预报和观测降水的空间分布，还采用了国家气象信息中心卫星、雷达和自动气象观测站三源融合的网格降水分析产品(CMPA)，潘旸等(2018)研究表明三源融合网格降水分析产品精度高于任何单一来源降水产品，同时也优于地面-卫星二源融合产品，在秦岭及周边地区CMPA与观测降水的年平均偏差最大为-0.05~-0.02 mm，均方根误差在0~0.2 mm，能够很好地刻画秦岭及周边地区的降水特征，代表性和适用性好。模式数据选取每天12时(文中无特别说明，均为世界时)的120 h预报时效的ECMWF高分辨率确定性降水预报，空间分辨率为0.125°×0.125°。考虑实际业务应用，采用双线性插值方法将模式降水插值成与CMPA网格降水量融合产品一致的空间分辨率(0.05°×0.05°)，插值后在模式原有输出格点上的数值不变。

研究范围选定为秦岭及周边区域(31°~40°N、103°~113°E)。由于模式对不同气候背景下降水的预报性能可能存在差异，除了在整个区域统一订正外，还根据重点关注区域暖季降水的主模态特征和降水气候区划(潘留杰等，2018；缪启龙等，1988)，分别进行降水订正，以期获得好的预报效果。图 1给出了重点研究区域的分区方案，图中三个分区分别为Ⅰ区：陕北黄土高原，Ⅱ区：关中平原，Ⅲ区：陕南秦巴山地。

2 方法

本文使用的检验评分主要包括晴雨预报准确率ACC(accuracy)、暴雨预报TS(threat score)评分，同时还计算了预报降水频率(FF)、观测降水频率(OF)和预报偏差(Bias)。晴雨和暴雨采用不同检验评分，是因为对晴雨来说，降水量较小的情况下漏报可能对人们生产生活影响不大，预报准确率对生产生活更有意义，暴雨漏报往往造成非常严重的损失而采用TS评分。公式如下：

$ \begin{array}{l} ACC = {\rm{ }}\frac{{A + D}}{{A + B + C + D}}{\rm{ }}, \\ \;\;\;\;\;\;\;TS = {\rm{ }}\frac{A}{{A + B + C}} \end{array} $

(1)

$ \begin{array}{l} FF = {\rm{ }}\frac{{A + C}}{{A + B + C + D}}{\rm{ }}, \\ OF = {\rm{ }}\frac{{A + B}}{{A + B + C + D}}{\rm{ }}, \\ Bias = {\rm{ }}\frac{{A + C}}{{A + B}}{\rm{ }} = {\rm{ }}\frac{{FF}}{{OF}}{\rm{ }} \end{array} $

(2)

式中：A为成功预报降水的次数, B为漏报的次数, C为空报的次数, D为正确预报无降水的次数。

通过观测提供的信息可以逐步地消除模式预报相对观测降水的系统性偏差。然而由于降水量具有非高斯分布的特性，不能直接使用降水量值，而是采用预报和观测降水的频率分布来评估模式的降水预报偏差，进而进行订正。计算时首先按阈值升序排列计算区域内预报和观测降水超过阈值的累积频率分布函数CDF，然后通过卡尔曼滤波方法来进行降水量累积频率分布函数CDF更新，其表达式为：

$ \overline {CD{F_{i, j}}} = \left({1 - W} \right)\overline {CD{F_{i, j - 1}}} + W(CD{F_{i, j}}) $

(3)

式中：$ \overline {CD{F_{i, j}}} $是在第j天第i个阈值的CDF的递减平均，$ \overline {CD{F_{i, j - 1}}} $是之前j-1天的递减平均，第j天第i个阈值预报和观测的CDF_{i, j}在数值上分别为FF_{i, j}、OF_{i, j}。W是递减权重，值域范围为0~1，简单地用近似时间滑动窗来定义，其表达式为：

$ W = {\rm{ }}\frac{1}{{nd}}{\rm{ }} $

(4)

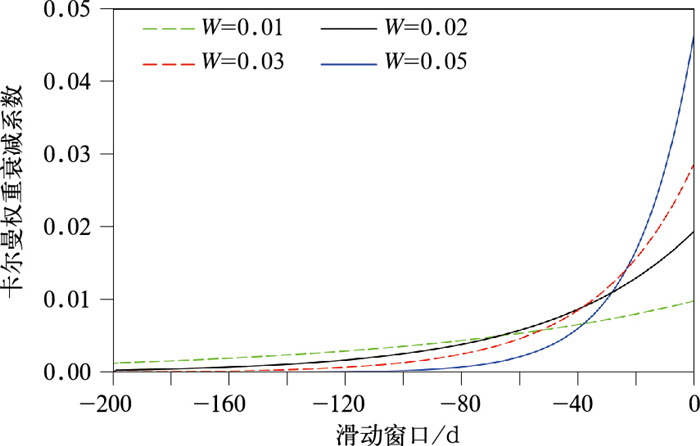
式中：时间滑动窗nd(或者递减权重$ \frac{1}{{nd}}$)是根据距离预报日期远近来调整其对CDF影响大小的权重，具体如图 2所示。对于第j天，前面j-1天的$ \overline {CD{F_{i, j - 1}}} $在$ \overline {CD{F_{i, j}}} $中所占的权重为1-W，对式(3) 产生的迭代过程来说，前面的j-k天的CDF_{i, j-k}对$ \overline {CD{F_{i, j}}} $的贡献为(1-W)^k，在k趋于无限的时候，其贡献越来越小，最终接近于零，因此，递减权重越大，递减速度越快，这也表明最新数据的权重最高，历史数据的权重减小。以50天的训练窗口为例，最新数据的权重W为0.02，其次为0.019 6，0.019 2，…，从而方法能够根据观测自适应捕捉数据流的动态变化信息。

构建完成降水量动态累积频率分布函数后，就可以对模式预报进行调整。预报和观测降水频率采用式(3)中更新的$ \overline {CD{F_{i, j}}} $值作为累积频率分布，针对一个原始的预报值，来为其分配一个具有相同频率的观测值，利用预报和观测值的CDF配对，评估预报系统偏差。假定选定阈值预报的CDF高于观测的CDF，模式降水预报偏多，对频率订正来说，当匹配到与观测降水频率一致时，相当于调低模式的降水频率，数值上等同于调小模式的预报降水量。实际计算时，针对不同格点上的降水量，使用两次线性内插来导出订正系数，数学上等同于使用两个数据点的多项式插值。譬如给定降水阈值向量T (n)，T₁，T₂，…，T_n按x轴的方向升序排列，每一个阈值上的观测CDF向量O(n)，O₁，O₂，…，O_n作为纵坐标，校准阈值向量为T^*(n)，T₁^*, T₂^*, …, T_n^*是基于在降水阈值T上的预报CDF值F(n)，F₁, F₂, …, F_n通过第一次线性内插获得，这里n是矢量的长度，因此n对(O，T)线性内插得到目标值(F，T^*)，这意味着预报在T_i^*上的CDF等于观测在T_i的CDF，表达式如下：

$ \begin{array}{l} \mathit{\boldsymbol{O}}{_1}\left({{\rm{ }}\mathit{\boldsymbol{T}}{_1}} \right) = {\rm{ }}\mathit{\boldsymbol{F}}{_1}\left({{\rm{ }}\mathit{\boldsymbol{T}}{_1^*}} \right)\\ \mathit{\boldsymbol{O}}{_2}({\rm{ }}\mathit{\boldsymbol{T}}{_2}) = {\rm{ }}\mathit{\boldsymbol{F}}{_2}({\rm{ }}\mathit{\boldsymbol{T}}{_2^*})\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \mathit{\boldsymbol{O}}{\mathit{\boldsymbol{}}_n}({\rm{ }}\mathit{\boldsymbol{T}}{_n}) = {\rm{ }}\mathit{\boldsymbol{F}}{_n}({\rm{ }}\mathit{\boldsymbol{T}}{_n^*}) \end{array} $

(5)

实际计算时所选阈值在第一次插值中使用了对数变换，此外，定义订正系数R_i为订正阈值与其相关阈值的比率(例：R_i= T_i^*/ T_i, i=1, …, n)。重复前面的步骤，那么每一个格点上的预报原始值都会有一个订正系数R(订正预报相对于原始预报的比率)，从而实现对网格预报中所有格点上的降水进行订正。

3 模式检验

模式的降水预报频率相对观测来说，可能在不同时间尺度上存在非常大的不同，因此降水订正之前，首先需对ECMWF模式降水预报的频率预报表现做简单评估。图 3给出了研究时段内不同预报时效上ECMWF模式预报频率的预报表现。为了显示清楚，降水频率在不同阈值上的分布采用了对数坐标。对比整个时段预报和观测降水的频率分布(图 3a)，可以看到降水量低于15.0 mm时模式降水预报频率显著偏多，降水量超过35.0 mm则预报频率明显偏少，两者在23.0 mm左右达到一致。但这种频率分布在不同的季节还存在显著不同(图 3c)，预报和观测频率曲线在春、夏、秋、冬季节的交点分别在25.0、10.0、33.0和35.0 mm左右，表明不同季节模式预报频率相对于观测存在显著的差异。

以往有研究工作采用频率匹配法将预报频率拟合到观测频率上来对降水进行订正。但事实上，由于模式降水预报存在位置、强度、时间等各种偏差，在预报和观测降水频率一致的情况下，并不一定能够得到最好的降水预报表现，为此定义最佳频率为不同预报时效上晴雨ACC和暴雨TS评分达到最高时的模式降水预报频率。本文最佳降水预报频率是通过逐步逼近法(张宏芳等，2014；2017)获得的，具体做法是以0.1为步长，进行观测降水频率倍乘，研究中采用倍乘的范围为0.6~2.0，这样模式预报降水就调整到了与观测频率不同倍数上，然后检验在哪个倍乘频率上的晴雨和暴雨预报评分相对观测降水最高，即为最佳频率。

晴雨(图 3b)和暴雨(图 3d)的观测降水频率显示，由于采用的模式数据为每天12时的120 h预报时效的ECMWF高分辨率确定性降水预报，检验的是逐12 h的24 h累计降水量预报表现，即预报时效分别为24 h，36 h，48 h, …, 120 h的前24 h累计降水量，这样就分别对应到00时和12时过去24 h的观测降水量，而这两个时段的降水频次是不同的，因此观测频率不是直线。对比可以发现晴雨模式最佳预报频率较观测明显偏低(图 3b)，特别是在84~120 h偏低更为显著，24~120 h晴雨最佳预报频率比观测低4.5%~9.2%，因此，期望获得较高的晴雨ACC，预报频次略小于观测，可能有更好的预报表现。与此对应(图 3d)，当暴雨预报TS评分达到最佳时，其预报频次较观测明显偏高，24~120 h暴雨最佳预报频率比观测高2.5%~4.3%，这意味着提高暴雨预报频率有可能获得更好的TS评分。

检验事实表明由于模式预报相对观测降水的位置或时间错位，在预报降水频率和观测一致的条件下，不一定能够得到最高的预报评分。相对订正到观测频率，订正到最佳频率可能能够获得更好的预报效果，为此，本文除了将模式预报降水订正到观测频率外，还将模式降水预报订正到最佳频率，将观测频率相对于最佳频率的倍乘系数定义为修正因子F。需要说明的是，这里的修正因子F和前文中的订正系数R是不同的，修正因子是为了将模式降水预报订正到与观测降水频率不同倍数上而采用的放大或缩小系数，而订正系数R是由于在观测降水频率计算过程中，采用了不同的阈值对降水场进行分段，在两次双线性插值过程中，当模式预报降水没有落在阈值上时采用的订正系数。此外，尽管需要对观测降水频率倍乘，但实际计算中，针对不同阈值的分段降水分别修正，订正后降水场中的值与模式原有降水场中的值是一一对应的，因此不需要再次融合。

4 结果分析 4.1 个例预报

订正方法在降水个例上的预报表现，能在一定程度反映方法的预报效果，因此在给出详细的长时段统计结果之前，先用两个个例简单表述订正效果。图 4为2019年9月发生在陕西关中、陕南的一次强秋雨天气过程的ECMWF模式降水预报和订正后的结果，可以看到9月13日12时至9月14日12时，陕西境内出现了大范围的降水天气，CMPA三源融合观测降水给出的强降水主要出现在关中和陕南的中西部(图 4a)，从所选出的388个自动站观测值来看，149个站24 h降水量超过50 mm，12个站超过100 mm，最大降水出现在汉中市南郑县法镇(147.8 mm)。模式预报ECMWF前24 h的降水预报基本没有预报出暴雨区(图 4b)，ECMWF在13日00时的降水预报(图 4c) 大雨区和观测基本一致，但暴雨预报范围明显偏小，仅在陕西南部和四川北部预报出了小范围暴雨区，暴雨区面积不足观测的1/5。

采用50天滑动窗口期，即递减权重W为0.02来计算降水卡尔曼的累积频率，并根据观测降水和预报降水对应的累积卡尔曼频率进行降水订正，其结果显示，无论是订正到观测频率或最佳频率都能显著提高降水的预报表现。从前24 h的降水预报来看，订正前(图 4b)晴雨ACC为0.87，暴雨TS评分为0，订正后对暴雨漏报的情况有明显改善(图 4d)，TS评分为0.125，但晴雨预报ACC略有下降，为0.835。13日00时起报的降水预报无论是晴雨或者是暴雨，相对于12日12时起报的都有改善，晴雨ACC为0.893，暴雨TS评分为0.08。采用卡尔曼方法订正到观测频率后(图 4e)暴雨TS评分达到0.253，预报技巧明显提高。而订正到最佳频率(图 4f)效果则非常理想，晴雨ACC为0.95，暴雨TS评分达到0.73。

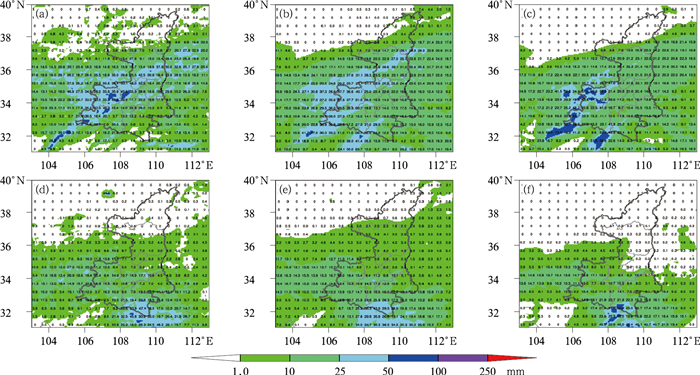
图 5给出另一个降水预报订正个例，2019年5月6—7日研究区域内出现了大范围的系统性降水天气(图 5a)，6日12时至7日12时，关中和陕南西部出现了大雨，局地暴雨。从ECMWF模式的降水预报来看，模式整体较好地预报了降水的空间形态(图 5b)，大雨区的范围和观测基本一致，主要不足在于强度偏小，仅在四川北部预报了零星暴雨点。CMPA降水显示关中西部和陕南西部都出现了局地暴雨。从订正结果来看(图 5c)，方法较好地调整了关中和陕南西部的降水量级，给出了较大范围的暴雨区，但在位置上有偏差，同时订正结果大雨和小雨的预报范围都有所减小。张宏芳等(2014；2017)表明，模式普遍有小量级降水预报偏大、大量级降水预报偏小的现象，本订正对这种现象有所改善，提高了模式降水预报的标准差，6日12时至7日12时模式原有预报(图 5b)降水标准差为10.78 mm，订正后为12.63 mm，观测为12.2 mm，订正后的降水预报标准差较观测略偏大，但和观测降水标准差的接近程度显著优于原模式预报降水。从7日12时至8日12时的降水订正结果(图 5f)来看，方法订正效果与前一日基本类似，对陕北南部小雨区降水量向下做了调整，对陕南地区的大雨区向上调整，但从订正后降水量空间分布的直观表现来看，在陕北南部的降水订正调整幅度偏大。陕南东部的降水调整后尽管量级与观测更加一致，但在暴雨的位置上仍有偏差，其暴雨预报评分并不理想。定量检验6日订正前、后的晴雨ACC分别为0.863和0.926，提高了0.063，暴雨TS评分订正前为0.0，订正后为0.06，无论是从直观效果还是定量检验，都有好的表现。对于7日来说，订正前、后的晴雨ACC分别为0.88和0.91，订正后尽管ACC提高，但直观上效果并不好，在暴雨预报方面，两天的TS评分均为0.0，没有订正正效果。

4.2 统计结果

本文在计算模式卡尔曼动态降水频率后，采用两种统计方法分析模式的预报表现：①利用一个修正因子F，放大或缩小模式与观测匹配的卡尔曼降水频率，并采用逐步逼近的方法，统计在何种情况下晴雨或暴雨的预报评分能够达到最好；②根据降水的气候背景进行分区，统计分区前后的模式降水预报表现。

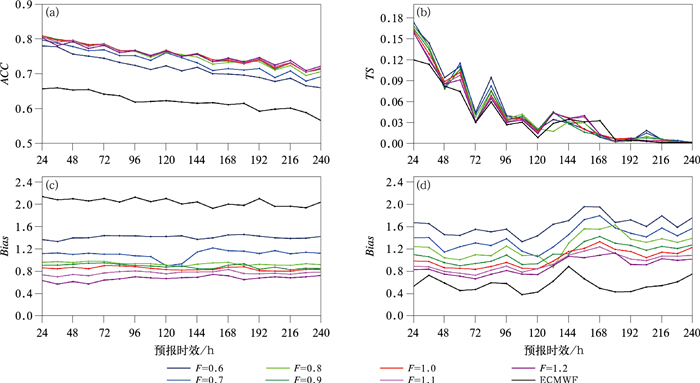
图 6给出了ECMWF模式在不同预报时效上的原始预报评分和基于卡尔曼动态频率订正到修正频率上的降水预报表现。可以看到，ECMWF在晴雨预报评分方面的主要表现是降水预报偏多(图 6c)，整个时段上预报相对于观测的频次偏多2倍左右，ECMWF的原始晴雨ACC维持在66%以下(图 6a)，频率订正后，显著减少了晴雨预报频率(图 6c)，增大了暴雨预报频率(图 6d)，24 h晴雨ACC增大到80.3%，暴雨TS评分则为0.161。频率倍乘后的预报评分显示，不同修正因子订正后可以进一步改变模式的预报偏差，从而影响降水预报表现，24 h预报时效上，修正因子F为0.8或0.9时，晴雨预报中降水的频率为观测频率的0.95倍左右，其ACC评分整体能够再提高1.5%；修正因子F为0.6或0.7时，暴雨预报频率高于观测1.5倍左右，暴雨TS评分较订正到观测频率再提高1.3%。在其他预报时效上略有不同，但采用合适修正因子，可以在模式降水频率匹配到观测降水的基础上，再次提高模式降水的预报表现。统计发现，24~120 h，暴雨预报偏差在1.5左右，晴雨预报偏差维持在0.95左右，晴雨ACC和暴雨TS评分较订正到观测频率分别提高了1%~5%和1%~3%。

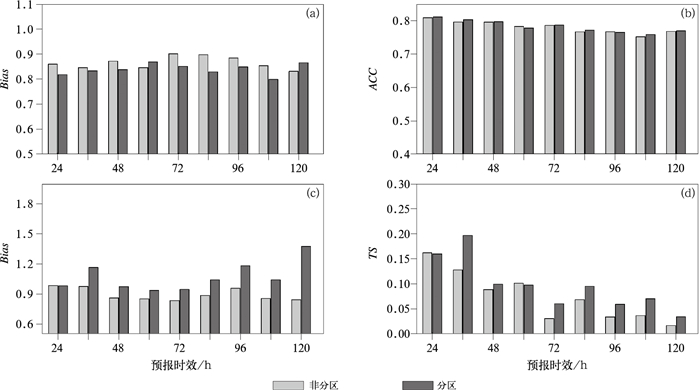
图 7给出了按照图 1的分区方案，采用卡尔曼动态频率分别在三个区域上降水订正，然后再进行融合后的降水预报表现。可以看到，在多数时段，采用分区方案晴雨预报偏差相对于未分区都有降低，表明模式在晴雨预报中的降水预报频率有所降低(图 7a)。采用分区方案后的晴雨ACC相对于未分区来说(图 7b)，整体略有提高或持平，但提高幅度非常微小，多数时段提高的幅度仅为0.01左右，分区方案对提高晴雨ACC效果并不明显。从分区前后的暴雨预报偏差来看(图 7c)，分区前暴雨预报频率接近于1或略低于1，分区后多数时段暴雨预报偏差增大，特别是在36 h、96 h、120 h时效上，增大非常显著。暴雨预报TS评分相对于未分区整体提高，特别是在36 h暴雨TS评分从未分区前的0.128提高到0.182，改善效果明显，这也是业务应用最为重要的时段，非常有实用意义。Zhu and Luo(2015)研究认为，分区太小样本数过少的情况，不利于提高模式的降水预报评分，本文观点与其一致，但在降水气候特征有显著差异、同时样本数较大的情况下，适当分区可以在一定程度上获得正的订正效果。

5 结论与讨论

基于2019年1月至2020年2月秦岭及周边地区98个县级观测站和290个无人自动气象站的24 h累计降水观测资料，客观检验ECMWF细网格模式的降水预报表现，并采用卡尔曼动态频率方法对ECMWF网格预报降水进行订正，主要结论如下：

(1) ECMWF模式对低量级降水的预报频率显著偏多，高量级降水的预报频率明显偏少，模式降水预报频率和观测频率曲线存在交点，研究时段两者全年降水频率在23.0 mm左右达到一致。但在不同季节上，模式降水的预报频率和观测显著不同，春、夏、秋、冬季节预报和观测频率曲线的交点分别在25.0、10.0、33.0和35.0 mm左右。

(2) 由于模式的降水预报存在位置、强度、时间等各种偏差，在预报和观测降水频率一致的情况下，并不一定能够得到最好的预报表现。统计发现，ECMWF模式24~120 h的晴雨和暴雨最佳预报频率分别低于观测4.5%~9.2%和高于观测2.5%~4.3%。

(3) 卡尔曼滤波方法根据给定的滑动窗口，动态修正模式降水预报偏差。从个例订正结果来看，该方法对模式小量级降水预报偏多的情况有明显的抑制，同时显著提高了暴雨的预报频率，订正后降水预报的标准差与观测更加一致，具有明显的订正效果。

(4) 针对预报评分达到最高时，最佳预报频率和观测频率之间存在一个差值的检验事实，采用修正因子，将模式降水小雨预报频率订正到较观测略偏少、暴雨预报频率订正到较观测略偏多。结果表明24~120 h，暴雨预报频率高于观测1.5倍(Bias=1.5)左右，晴雨预报偏差维持在0.95左右，晴雨ACC和暴雨TS评分较订正到观测频率分别提高了2%~5%和1%~3%。

(5) 按照降水特征进行分区，分别采用卡尔曼动态频率进行降水订正，然后融合，结果表明分区方案可以显著提高暴雨预报的TS评分，但对晴雨ACC的贡献不显著。

文章利用卡尔曼动态频率方法，对ECMWF模式的预报降水进行频率订正，结果表明该方法对晴雨预报的准确率和暴雨预报TS评分都有提高，但本质上来说，卡尔曼动态频率订正只是一种降水量级的强度订正方法，在模式降水位置预报正确，但量级有明显偏差的情况下，订正效果较好，如果模式降水的位置或时间预报有偏差，卡尔曼动态频率对此无能为力。理想情况下，动态频率订正方法将频率偏差控制在1(Bias=1)左右，预报降水位置与观测吻合较好时，可以获得最佳暴雨TS评分，然而由于降水位置偏差，增大暴雨预报频率到观测频率的1.5倍左右，减少漏报来提高暴雨TS评分是一种可行的订正方法，但不可避免地会增加空报。如何在提高暴雨预报TS评分的同时抑制空报，是降水订正需要解决的一个关键问题。这一方面有赖于模式预报性能提高，减少降水场初始预报误差，事实上，从最新模式降水预报来看，ECMWF降水强度预报误差不断减小，基于卡尔曼动态频率的降水预报订正方法所取得的效果会随着模式分辨率和降水强度预报性能不断提高而逐步下降；另一方面，可以采用面向对象方法或目标法来识别降水场中的空间降水对象，找出强降水空间位置预报误差的统计规律，在订正强降水空间位置的基础上，再次开展频率订正，有望在将模式暴雨预报频率调整到与观测基本一致或略高于观测的情况下获得最优的暴雨TS评分，这也是降水订正工作后期需要重点发展和研究的方向。