西部山地突发性暴雨是我国重大自然灾害之一,其预警与防范是国家防灾减灾重大而迫切的战略需求。西部山地突发性暴雨的预报难点,除自身的非线性特征外,与长江流域等其他区域的暴雨相比,具有更加复杂的环境条件:如观测资料缺乏、地形陡峭、下垫面状况复杂等,加之模式不可避免的缺陷以及初始条件的有限误差(Kalnay, 2005),单一模式对西部山地暴雨的预报存在着较大的不确定性,而发展集合预报技术是目前解决预报不确定性的重要手段。
目前对短期不确定过程的研究主要集中在初值和模式的不确定研究方面。初值扰动方法以奇异向量法(SV)和增长模繁殖法(BGM)为代表,对于模式不确定性的研究多是通过不同物理方案的组合或采用不同模式的组合(杨学胜,2001;杜钧,2002)。近年来,随机物理过程作为多物理过程的一种可能的替代方案,在模式不确定性的研究中越来越被重视(杜钧和李俊,2014;陈涛等,2019)。集合预报模式随机物理扰动方法(Bowler et al, 2008;Berner et al, 2009;Palmer, 2012)相比于多物理方案具有更一致的集合,描述的是模式物理过程随机误差引起的预报不确定性(Jankov et al, 2017)。目前主要有三种具有代表性的模式随机物理扰动方法:(1)利用随机扰动净倾向来表征模式不确定性(Palmer et al, 2009)的模式随机物理倾向扰动(SPPT),可改善集合离散度与概率预报技巧(袁月等,2016;Leutbecher et al, 2017);(2)利用随机扰动流函数来表征模式不确定性的随机动能后向散射补偿法(SKEB),可改进集合离散度不足的问题(Shutts,2005;Berner et al, 2009);(3)利用随机扰动物理参数化方案内的关键参数来表征各参数不确定性(Ollinaho et al, 2017)的随机参数扰动(SPP)方法。SPP表征在物理过程中靠近其源的参数化趋势的一些关键随机误差(陈静等,2003;Bowler et al,2008;Baker et al,2014;Jankov et al,2017),相对于SPPT和SKEB的优点在于可以保持模式的物理一致性,保持确定性参数化所遵循的水分、动量和能量的局部预算守恒,且不会引起计算不稳定。Jankov et al(2017)研究表明SPP和SPPT、SKEB方案的组合较多物理过程集合预报法能得到更大的集合离散度,并指出SPP与其他随机物理扰动方法组合可替代多物理过程法,进一步验证了SPP方案应用到高分辨率集合预报的可行性。随机物理参数扰动SPP方法近年来受到广泛关注和重视(王璐和沈学顺,2019)。
随着模式的发展,物理过程越来越详尽。其中,大气边界层是直接受地表强迫影响的对流低层大气(Stull, 1988),其参数化方案描述了边界层及自由大气的动量、热量、水汽等物理量的垂直湍流输送, 陆面过程参数化方案描述地气之间水汽、热量和动量的交换(周文艳等,2019),两者直接影响地气间热量、水汽、动量的输送,进而影响暴雨发生发展的热力、动力和水汽条件,影响暴雨过程的模拟。研究表明,边界层高度日变化振幅随海拔高度的增加而增大(徐桂荣等,2014),西部山地地形复杂,边界层变化很不均一,模式中的边界层方案对于次网格湍流过程、陆面过程方案及地气间的能量交换很难准确表征,而不准确的来源之一是方案中参数的不确定。随机参数扰动通过随机扰动物理过程参数化方案中的不确定性关键参数或变量来表征预报的不确定性,提供可能性预报。
Ollinaho et al(2017)指出随机型时空尺度参数的设置会影响随机参数扰动方法的概率预报效果,随机型去空间相关系数值越大,截断波数越小,扰动的空间尺度越大,而去时间相关系数值越大,两个时次间随机场相关性越大,随时间变化频率越低。已有的工作多为对SPPT和SKEB方案的参数敏感性的研究(蔡沅辰等,2017;闵锦忠等,2018;张涵斌等,2019),对SPP方案的相关参数敏感性的研究相对较少,且多集中在对流参数化相关经验参数的随机扰动上(谭燕和陈德辉,2007;李俊等,2015;智协飞等,2020),而边界层方案和陆面过程方案中同样存在很难准确表征的参数和变量,是模式不确定性的重要来源,而一个集合预报系统通常应包含多种不确定性来源并采用相应的扰动技术(杜钧和李俊,2014),因此,为探索不同随机型时间尺度和空间尺度参数的设置对随机扰动边界层、陆面过程参数方案集合预报效果的影响,了解上述两种物理方案随机扰动的增长特性,为今后多种物理方案随机扰动在山地暴雨集合预报的综合运用提供科学依据,本文使用WRF v3.9分别基于随机边界层和陆面过程参数扰动方案构造3 km水平分辨率的山地暴雨集合预报。通过2018年5月21—22日我国西南山地一次特大暴雨的随机参数扰动集合预报敏感性试验,对比评估集合预报效果及其对时空尺度参数设置的敏感性,获取适合西部山地暴雨的时空扰动参数,进而为综合运用多种随机物理方案、科学发展适用于山地暴雨集合预报系统的模式扰动技术提供依据。
1 随机参数扰动方法 1.1 MYNN边界层参数化方案及其不确定性参数MYNN边界层参数化方案是基于Mellor and Yamada(1974)提出的M-Y二阶湍流动能闭合模型发展起来的。与M-Y模型相比,Nakanish(2001)主要发展了浮力作用的计算,提出了一个新的计算湍流尺度的L方程,形成了MYNN Level-3边界层方案。该方案具有更真实的湍流运动表征,使用了较少的试验和观测得到的闭合常数(Huang and Peng, 2017),但L方案中近地表的、依赖边界层厚度的、受浮力效应限制的三个长度尺度仍存在不确定性(Nakanish,2001)。此外,MYNN Level-3方案中还存在次网格云和粗糙度两个不确定性参数,次网格云为Nakanishi and Niino (2006)在MYNN Level-3方案中融入凝结物理过程引入的,代表了边界层内的浅积云,粗糙长度则表征的是地表与大气的相互作用,反映地表对风速的消减作用,直接影响边界层的发展。
本研究中针对MYNN Level-3方案中湍流混合长度、次网格云和粗糙长度等不确定参数,采用随机参数扰动(SPP)方法进行随机扰动,以下简称SPPM。SPPM中直接扰动湍流混合长度、次网格云两个诊断量,而热量和湿度粗糙长度通过扰动Zilintikevich系数Czil来实现(王璐璐等,2020)。SPPM方案中对参数的扰动影响着边界层及自由大气中次网格热量、水汽、动量等物理量的垂直湍流输送,进而影响暴雨发生发展的热力、动力和水汽条件,影响暴雨过程的模拟。
1.2 RUC陆面过程参数化方案及其不确定性参数RUC(rapid update cycle)陆面方案(Smirnova et al,2000)包含了6层土壤模式,充分考虑了土壤温度和湿度的变化,在保持水和能量平衡的基础上细致地考虑了地气间动量、感热、潜热和水汽输送等物理过程,与不同下垫面的地表特征密切相关。不同下垫面在模式里表现为不同的地表反照率、粗糙度、土壤孔隙度、最小叶孔阻抗值,其中,地表反照率是指地表反射的太阳辐射通量与入射的太阳辐射通量的比值,地表粗糙度指下垫面的粗糙程度,土壤孔隙度为土壤孔隙占土壤总体积的百分比,最小叶孔阻抗为植被通过叶孔蒸散传输水分时所受阻力的大小(倪悦,2013)。这些参数的差异根据植被类型来区分,目前仍存在不确定性。
本研究中针对RUC方案中土壤孔隙度、地表反照率、地表粗糙度和最小叶孔阻抗等不确定参数,采用SPP方法进行随机扰动,以下简称SPPR方法。SPPR方法中对参数的扰动直接或间接影响着地气间热量、动量和水汽的输送,如地表反照率的扰动直接影响陆气之间能量的分配,地表粗糙度的扰动主要影响大气的动能分配,土壤孔隙度的扰动影响土壤湿度改变陆气之间能量和水汽的交换,最小叶孔阻抗的扰动影响植被的蒸腾作用和植被周边环境场的能量分配(陈海山等,2014),进而对地表通量、环流形势和水汽场产生影响,最终使得降水发生变化。
1.3 随机参数扰动方法及参数设置SPP方法是针对模式物理参数化方案中不确定的参数X加入时空相关的随机扰动(Jankov et al,2017),可以用下式表示:
| $ X_{p}=[1+r(x, y, t)] X $ | (1) |
式中:Xp为扰动后参数值,r(x,y,t)表示时空相关的随机扰动场。
| $ r(x, y, t)=\sum\limits_{k=-K / 2}^{K / 2} \sum\limits_{l=-L / 2}^{L / 2} r_{k, l}(t) \mathrm{e}^{2 \pi i\left(\frac{k x}{X}+\frac{l y}{Y}\right)} $ | (2) |
式中:k和l分别代表经向(K+1)和纬向(L+1)个波数分量,
| $ r_{k, l}(t+\Delta t)=(1-\alpha) r_{k, l}(t)+g_{k, l} \varepsilon_{k, l}(t) $ | (3) |
式中:α是由设定的去时间相关尺度τ决定,两者关系为τ=Δt/α;εk, l(t)是一个复杂白噪音过程;gk, l是依赖波数的噪音振幅,计算参考Weaver and Courtier(2001),具体公式如下:
| $ g_{k, l}=F_{0} \mathrm{e}^{-4 \pi \kappa_{k}, l^{2}} $ | (4) |
| $ F_{0}=\left\{\frac{\eta_{k, l}^{2}\left[1-(1-\alpha)^{2}\right]}{2 \sum\limits_{k} \sum\limits_{l} \mathrm{e}^{-8 \pi \kappa_{k, l}{ }^{2}}}\right\}^{1 / 2} $ | (5) |
式中:
扰动形态由格点标准偏差η、去空间相关尺度κ和去时间相关尺度τ三个参数确定。目前关于这三个参量值该如何设定并没有一致结论,但是根据SPP方案扰动形态的原理可知,去空间相关尺度κ和去时间相关尺度τ表示随机序列的时、空变化速率,控制扰动的空间结构变化。已有的一些研究表明,随机扰动的时空参数与天气过程相关,其设置应与天气系统的尺度相适应(闵锦忠等,2018),而且扰动结构和扰动振幅相比,前者更重要(李俊等,2009;杜钧和李俊,2014)。为探究适用于我国西部山地暴雨的随机扰动参数调整规律,本研究中的SPPM试验以Jankov et al(2017)的工作为参考(该工作中设定格点标准偏差η、去空间相关尺度κ和去时间相关尺度τ的默认值分别为0.15、700 km和6 h),与扰动振幅相关的格点标准偏差η保持0.15不变,重点研究与随机扰动结构变化关系密切的时空扰动参数(去空间相关尺度κ和去时间相关尺度τ),并结合2018年5月21—22日四川、重庆地区这次山地暴雨过程的时空特征(强降水时段集中,与中尺度系统的移动紧密相关,具体见2.1节个例简介),以及西部山地更复杂多变的边界层特征,在缺省参数的基础上,将去空间相关尺度由700 km减小为70 km进行试验, 将去时间相关设定为6 h、3 h进行敏感性试验;同上,在本研究中的SPPR试验中,也参照WRF中的默认值,将SPPR去空间相关尺度、去时间相关尺度设定为500 km/50 km、6 h/3 h进行敏感性试验,而与扰动振幅相关的格点标准偏差η与原试验的缺省值保持一致。
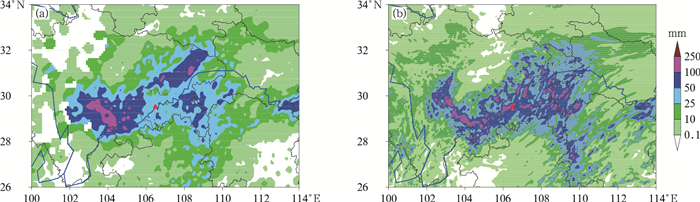
2 试验方案设计 2.1 个例简介2018年5月21—22日受500 hPa低槽和西南涡东移影响(图略),在四川、重庆地区发生了一次山地特大暴雨过程,5月21日12时至22日12时(世界时,下同)四川西南部到重庆西北部大部分地区24 h累计降水量达到25 mm以上,超过100 mm的国家级气象站点有324个,最大降水量站点为四川省乐山市沐川县芹菜坪站(海拔高度为1 015 m),达到363.9 mm,另外峨眉山市九里镇兴阳村(海拔高度为785 m)和乐都新沟村(海拔高度为948 m)这两个站点降水量超过300 mm,最大小时雨强为114.8 mm ·h-1(峨眉山市双福镇露华村,海拔高度为668 m)。伴随西南低涡的东移,强降水中心依次位于四川盆地西南部(21日12—18时)、四川盆地东北(21日18时至22日00时)、重庆与湖北恩施交界处(22日00—06时),24 h雨带整体呈西南—东北走向,是一次较典型的具有山地背景的强降水过程(过程雨量见图 1a)。
|
图 1 2018年5月21日12时至22日12时(a)实况和(b)控制试验模拟的24 h累计降水分布 Fig. 1 Distributions of 24 h accumulated precipitation of (a) observation, and (b) control experiment simulation from 12 UTC 21 to 12 UTC 22 May 2018 |
本文采用WRF v3.9(Skamarock et al, 2005)对其进行数值模拟。控制试验(CTL)模式采用单层无嵌套,水平分辨率为3 km,水平格点数为699×699,垂直为51层,初始场与侧边界条件均由GFS全球预报资料提供,主要物理过程包括:Thompson云微物理方案、MYNN3边界层参数化方案、RRTMG辐射方案和RUC陆面过程方案等,关闭对流参数化方案。模式积分36 h(2018年5月21日00时至22日12时)。控制试验模拟的21日12时至22日12时24 h累计降水(图 1b)和实况对比,可见CTL模拟的雨带走势和实况较吻合,四川盆地西南部降水大值落区得到较好模拟,而重庆西北部降水大值区则在控制试验的模拟结果中偏弱,重庆东南部和湖北西南部的降水模拟偏大。
2.3 随机参数扰动试验设计随机参数扰动试验初始场与侧边界条件同样由GFS全球预报资料提供,模式设置与CTL相同,调整去空间相关尺度κ和去时间相关尺度τ设置(表 1),SPPM、SPPR分别对MYNN边界层参数化方案不确定的参数(湍流混合长度、次网格云和粗糙长度)和RUC陆面过程参数化方案不确定的参数(土壤孔隙度、地表反照率、地表粗糙度和最小叶孔阻抗)进行随机扰动,每组试验通过改变SPP中的随机种子生成8个扰动成员,与控制成员一起构成9个成员的集合预报。获得SPPM、SPPR最优去时、空相关尺度配置的基础,组合进行试验(记为SPPM+SPPR,根据后文的分析可知SPPM_70_6和SPPR_50_6各项评分相对较优,SPPM+SPPR试验即为SPPM_70_6和SPPR_50_6的组合),以探究在对流尺度中同时扰动MYNN边界层、RUC陆面过程方案参数的预报效果。
|
|
表 1 随机参数扰动试验及扰动形态设置 Table 1 The SPP experiments and stochastic perturbation pattern setting |
文中地面、高空变量检验采用欧洲中心全球第五代再分析资料ERA5作对比,降水检验采用国家气象信息中心0.1°×0.1°网格化逐时实况降水融合资料(沈艳等,2013)做对比。检验前使用双线插值方法将集合预报的变量插值成与实况和再分析资料一致的分辨率,文中所有地面参数定量评估均基于0.1°×0.1°的格点分辨率,高空参数定量评估均基于0.25°×0.25°的格点分辨率。本研究重点关注随机扰动边界层、陆面过程参数化方法在山地暴雨集合预报中的敏感性及其扰动效果,因此主要针对这次过程的主要降水时段(21日12时至22日12时,对应模式模拟12~36 h预报时段)和主要降水落区(图 1所示区域)进行检验分析。
3 集合预报效果检验与分析 3.1 近地面变量预报检验SPPM与SPPR方案主要表现了地面-近地层的湍流混合过程,其对近地面变量的预报产生着显著影响。因此首先对2 m温度、10 m U风和10 m V风的离散度、均方根误差(RMSE)和离散度/均方根误差值检验。离散度为集合成员与集合平均的标准偏差,在一定范围内离散度越大越能包含真实大气的各种可能性。RMSE检验预报场与分析场之间的差异,值越大则预报误差越大。对一个理想可信度高的集合预报系统,RMSE与离散度应该有相同的幅度与变化率(Berner et al, 2011)。
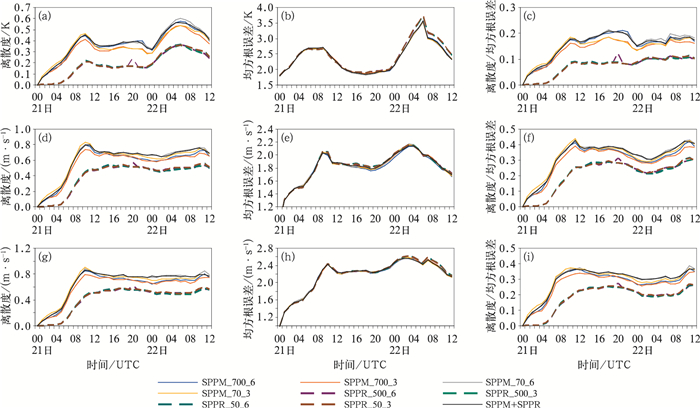
图 2展示了9组试验2 m温度、10 m U风和10 m V风的离散度、RMSE和离散度/均方根误差值评分,总体而言(图 2a、2d、2g),SPPM方案的离散度大于SPPR方案,表明扰动边界层方案能比扰动陆面方案获得更大的扰动能量。两种方案对温度和风场扰动的量级相当,其中温度扰动多在0~0.6 K,最大可达到0.602 K,风场扰动多在0~0.9 m·s-1,最大可以达到0.903 m·s-1。各组试验温度离散度增长随时间的演变趋势相似,均在积分的前12 h增长迅速,其后趋于平缓,在积分24 h稍有下降后又快速增长,可能与温度的日变化有关;各组试验风场离散度增长随时间的演变趋势也相似,均在积分的前12 h增长迅速,其后趋于平缓,风场的离散度在积分前12 h达到饱和,之后随着积分时间的增长变化不大。
|
图 2 各试验模拟的2018年5月21日00时至22日12时(a~c)2 m温度、(d~f)10 m U风和(g~i)10 m V风的(a, d, g)离散度、(b, e, h)均方根误差和(c, f, i)离散度/均方根误差值随时间的变化 Fig. 2 The spread (a, d, g), RMSE (b, e, h) and spread/RMSE ratio (c, f, i) of all experiments for the 2 m temperature (a-c), 10 m U wind (d-f), 10 m V wind (g-i) from 00 UTC 21 to 12 UTC 22 May 2018 |
在SPPM的4组试验中,固定去空间相关尺度对比不同去时间相关尺度试验的地面变量离散度可以发现,去时间相关尺度6 h的所有试验2 m温度离散度均高于3 h,说明SPPM中去时间相关系数的值越大,可以获得更大的离散度增长;在相同的去时间相关参数下,SPPM将去空间相关尺度由700 km调整为70 km时对2 m温度离散度有一定的增大。SPPM方案各地面变量与ERA5的均方根误差4组试验相差不大,离散度/均方根误差评分SPPM_70_6较其他3组试验评分最优。在SPPR的4组试验中,温度和风场的离散度和均方根误差都差异不大,离散度/均方根误差评分也相当,SPPR方案由于其扰动能量总体偏小,使得去空间和去时间相关参数的变化对其集合预报性能影响也相对较小。SPPM+SPPR组合试验与SPPM_70_6地面变量的离散度非常接近。
3.2 高空变量预报检验SPPM与SPPR方案对高空变量垂直分布的影响如何,在此检验了高空温度、U风场和水汽场集合预报效果。总体来看SPPM和SPPR方案各变量离散度大值中心在700 hPa以下,两种方案扰动呈现从低层向高层扩展的趋势。图 3展示了不同集合预报试验中在850 hPa高度层的温度、U风场和水汽场的平均离散度、均方根误差和离散度/均方根误差值随时间的变化。整体来看SPPM方案的离散度大于SPPR方案,表明扰动边界层方案比扰动陆面方案能获得更大的扰动能量。两种方案对温度、风和水汽扰动的量级相当,离散度增长随时间演变均在积分前12 h增长迅速。温度离散度在850 hPa、700 hPa(图略)迅速增长后趋于平缓,而500 hPa高度(图略)迅速增长后有下降趋势后缓慢增大,温度均方根误差850 hPa随着积分时间的增加呈增大趋势,700 hPa和500 hPa高度随积分时间的变化相对比较平缓;U风场离散度在850 hPa和700 hPa迅速增长后呈下降趋势,而在500 hPa积分12 h后变化较平缓,均方根误差在不同高度层差别较小;水汽离散度在850 hPa迅速增长后有增长趋势,在700 hPa迅速增长呈下降趋势,500 hPa积分12 h后变化平缓,均方根误差在850、700、500 hPa三个高度层大小差异不明显。SPPM的4组试验中,SPPM_70_6温度、U风场和水汽场的离散度、离散度/均方根误差评分最优,SPPR的4组试验中各高空变量的离散度评分相当。SPPM+SPPR组合试验高空变量在积分前24 h的离散度略高于SPPM_70_6,积分后12 h略低于SPPM_70_6,这种差异在850 hPa高度表现最为明显。SPPM、SPPR分别对MYNN边界层参数化方案不确定的参数(湍流混合长度、次网格云和粗糙长度)和RUC陆面过程参数化方案不确定的参数(土壤孔隙度、地表反照率、地表粗糙度和最小叶孔阻抗)进行随机扰动,边界层扰动相对陆面过程而言,其扰动更加深厚,因而其模式变量的离散度更大。

|
图 3 各试验模拟的2018年5月21日00时至22日12时850 hPa(a~c)温度、(d~f)U风和(g~i)水汽混合比的(a, d, g)离散度、(b, e, h)均方根误差和(c, f, i)离散度/均方根误差值随时间的变化 Fig. 3 Simulated changes of the spread (a, d, g), RMSE (b, e, h) and spread/RMSE ratio (c, f, i) of the 850 hPa temperature (a-c), U wind (d-f), water vapor mixing ratio (g-i) from 00 UTC 21 to 12 UTC 22 May 2018 |
边界层参数化方案描述了行星边界层及自由大气中次网格热量、水汽、动量等物理量的垂直湍流输送, 陆面过程参数化方案描述了地气之间水汽、热量和动量的交换,两者直接影响地气间热量、水汽、动量的输送,进而影响暴雨发生发展的热力、动力和水汽条件,影响暴雨过程的模拟。下文进一步对降水预报的结果进行检验。
3.3 降水预报检验集合预报与单一的确定性预报相比可以给出多种可能性及其发生的概率,下面对此次山地暴雨过程边界层(SPPM)和陆面过程(SPPR)参数随机扰动集合预报的降水结果进行多方面的检验评估。
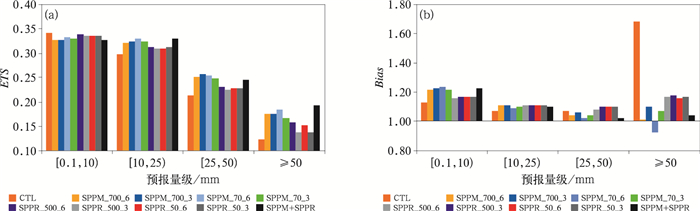
3.3.1 确定性预报(集合平均)检验杜钧(2002)指出评估集合预报效果好坏的一项重要指标是集合平均的检验,对集合平均的检验采用单一模式预报检验相同的方法。图 4给出21日12时至22日12时的24 h时间段内CTL、SPPM、SPPR、SPPM+SPPR共10组预报逐6 h降水的ETS评分,对降水的检验均为21日12时至22日12时这24 h内的4个6 h的预报样本累加到一起的总体评分。总体而言,除0.1 mm外,两种物理方案随机扰动的集合平均降水预报均优于控制预报,这表明尽管只采用了物理过程的随机扰动,集合预报系统的离散偏小(图 7),但还是可以获得优于单一控制预报的集合平均预报。此外,随机扰动边界层参数化方案(SPPM)ETS评分优于随机扰动陆面过程方案(SPPR),这与SPPM方案能获得更大的扰动能量(图 3)且扰动分布更合理有关(图 6,图 7b)。对比相同扰动方案不同扰动参数的试验,改变时空扰动参数对集合平均降水的影响相对较小,SPPM的4组试验中,除25 mm量级外,SPPM_70_6的ETS评分优于其他3组参数的试验。SPPR的4组试验中,SPPR_500_6和SPPR_50_6 ETS评分相当,并且略高于SPPR_500_3和SPPR_50_3。SPPM+SPPR组合试验中 < 50 mm的降水ETS评分与SPPM_70_6相当,≥50 mm的ETS评分明显优于各组试验。
|
图 4 集合平均和控制试验模拟的2018年5月21日12时至22日12时6 h累计降水的(a) ETS和(b) Bias评分 Fig. 4 ETS (a) and Bias (b) scores of 6 h accumulated precipitation from 12 UTC 21 to 12 UTC 22 May 2018 of the ensemble mean forecasts and the control experiment |

|
图 5 控制试验、集合平均与实况6 h累计降水的均方根误差 Fig. 5 RMSE of the 6 h accumulated precipitation in the control experiment and the ensemble mean forecasts versus the observation |
|
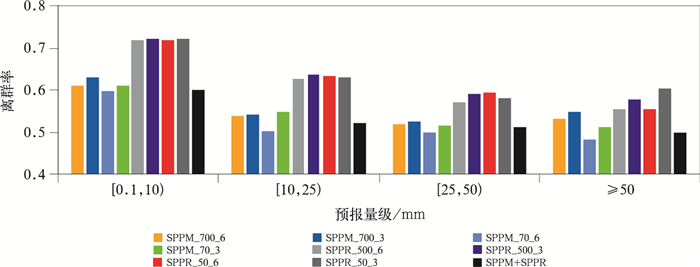
图 6 集合预报6 h累计降水量在不同量级上的离群率 Fig. 6 The outlier of the ensemble forecasts at different categories for the 6 h accumulated precipitation |

|
图 7 集合预报6 h累计降水的(a)Talagrand分布和(b)Talagrand分布与理想频率分布之间的概率均方差 Fig. 7 (a) Talagrand distribution and (b) the probability mean squared differences between the expected-probability and Talagrand distribution derived from the ensemble forecasts for 6 h accumulated precipitation |
图 5为9组试验集合平均降水预报和控制预报6 h累计降水量与实况之间的RMSE,其值可以反映不同参数试验中雨量的集合平均预报和实况之间的差距。如图所示,与图 4的ETS评分类似,9组不同参数的集合平均降水的雨量预报误差均小于控制预报,并且SPPM组试验的雨量预报误差小于SPPR组。在不同扰动参数的4组SPPM试验中,在相同的去空间相关参数下,6 h去时间相关参数的雨量预报误差均小于3 h的, 其中SPPM_70_6的RMSE值最小,即SPPM_70_6集合平均的降水强度预报最优。而在4组SPPR试验中,集合平均预报和实况的RMSE值相差不明显,这可能是SPPR试验和SPPM试验相比,其扰动的能量总体偏小,不同扰动参数得到的集合平均预报比较相近造成的。SPPM+SPPR的RMSE较SPPM_70_6略高,低于其他试验。
3.3.2 集合区间预报计算9组试验集合预报6 h累计降水在不同量级上的离群率,即实况大于集合最大成员或者小于集合最小成员的格点数占该实况出现总数的比例(李俊等,2020)。如图 6所示4个降水等级区间,随着实况降水量级的增大,降水集合预报的离群率都随之减小,但这种离群率随量级减小的趋势应是由样本数减少造成的,不能反映随量级越大预报效果越好。对比SPPM和SPPR两类扰动方案,SPPM组试验的离群率明显低于SPPR组试验,也表明SPPM方案能获得更大的扰动离散度,这与图 3和图 7的结论一致。SPPM组试验中,SPPM_70_6各降水量级上的离群率均最低。而在4组SPPR试验中,6 h累计降水在0.1~10 mm的实况离群率差别不大,在10~50 mm的实况SPPR_500_6离群率最低,≥50 mm以上的实况SPPR_50_6离群率最低。SPPM+SPPR离群率较SPPM_70_6差别不大,没有表现出明显的优劣势。
3.3.3 离散度检验在此采用Talagrand分布检验方法(李俊等,2015)对9组试验集合降水预报的离散度进行检验(图 7)。在SPPM的4组试验中,从实况落在集合区间之外的频率都大于区间之内可得集合预报的离散度均偏小,这是由于本文只采用了物理过程随机扰动方案,没有引入更多其他扰动。SPPM_70_6实况落在集合预报区间的频率较其他方案均大,这与3.3.2节离群率的结论类似,表明SPPM_70_6方案的集合区间预报能更好地包含实况,结合Talagrand频率分布与理想频率分布之间的均方差,SPPM_70_6概率均方差小,SPPM_70_6离散度分布更接近理想状态,优于其他3组集合预报。SPPR 4组集合预报中实况落在集合区间之外的频率同样都偏大,不同扰动参数对Talagrand分布的影响不如SPPM方案显著,这与图 5的结论类似,主要是由SPPR方案总体的扰动能量偏小造成的。相对而言,SPPR_50_6实况落在集合预报区间的频率较其他方案稍大,结合Talagrand频率分布与理想频率分布之间的均方差,SPPR_50_6概率均方差较其他3组试验稍小,其离散度分布更接近理想状态,优于其他3组集合预报。SPPM+SPPR的Talagrand频率分布和概率均方差评分较SPPM_70_6差别不大。
3.3.4 概率预报检验李俊等(2015)指出集合预报可以提供定量的概率预报,即从集合成员的预报中可以计算出某种天气发生的相对概率。Roberts and Lean(2008)提出的邻域空间检验方法FSS评分,可检验集合预报在不同空间尺度上的概率预报能力。当FSS=0时预报与实况完全不匹配,评分最低;但FSS=1时预报与实况概率一致,评分最高;当FSS≥0.5时,所对应的窗口尺度即为所谓降水预报的“可用预报尺度”(赵滨和张博,2018;李俊等,2020)。
图 8给出所有集合预报6 h累计降水不同降水量级在10、50、90、130 km邻域空间尺度上的FSS评分。9组试验6 h降水≥0.1 mm的量级,在10 km尺度的FSS评分达到0.75以上,且FSS评分随着邻域空间尺度增大而提高,即降水预报随着邻域空间尺度的增大能获得更高的概率预报技巧,这与李俊等(2020)结论一致。总的来看,SPPM各组试验FSS评分较SPPR高,其中SPPM_70_6试验6 h累计降水≥0.1 mm、≥10 mm、≥50 mm预报在不同邻域空间尺度上的FSS评分为SPPM方案中最高, SPPR各组试验FSS评分相差不大。SPPM+SPPR试验FSS评分较SPPM_70_6差别不大。

|
图 8 集合预报6 h累计降水预报在不同邻域空间尺度上的FSS评分 (a)[0.1, 10) mm,(b)[10, 25) mm,(c)[25, 50) mm,(d)≥50 mm Fig. 8 The FSS score on the different neighborhood spatial scales for 6 h accumulated precipitation by ensemble forecasts (a) [0.1, 10) mm, (b) [10, 25) mm, (c) [25, 50) mm, (d) ≥50 mm |
为进一步对比不同扰动参数下SPPR 4组试验概率预报的相对优劣,计算SPPR集合24 h累计降水预报在不同邻域空间尺度上的FSS评分(图略)。FSS评分演变与邻域空间尺度的演变趋势和图 8类似,其中24 h累计降水≥10 mm、≥50 mm预报不同邻域空间尺度上的FSS评分情况,SPPR_50_6较其他3组试验略高。
4 结论与讨论本文基于WRFv3.9模式探究了在山地暴雨集合预报中,使用SPP方法扰动MYNN边界层方案和RUC陆面过程方案参数对我国西南山地一次特大暴雨预报中影响。同时,在研究中构造了多组数值模拟试验调整SPP方法中的去时间相关尺度和去空间相关尺度,通过对地面气象要素、物理量垂直分布及降水检验进行对比分析,得到的主要结论如下:
(1) 随机扰动MYNN边界层方案(SPPM)和RUC陆面过程方案参数(SPPR)中,由于扰动的主要是地面和模式低层的变量,扰动能量从模式低层开始发展,并逐步向高层扩展,模式低层变量的离散度大于模式中高层。
(2) 随机扰动MYNN边界层方案和RUC陆面过程方案参数相比,扰动边界层方案能获得更大的扰动能量,因此SPPM比SPPR方案能获得更优的离散度分布,其集合平均预报和概率预报也优于SPPR方案。
(3) 不同的去空间相关参数和去时间相关参数会改变随机扰动的时空分布,进而影响集合预报系统的性能,就本次试验而言,集合预报系统对去时间相关参数的变化更敏感。SPPR方案由于其扰动能量总体偏小,因而上述两个参数的变化对其集合预报性能影响相对较小。
(4) 对于SPPM试验而言,通过系统的检验,SPPM_70_6在集合平均预报、离散度分布和概率预报技巧等方面均优于其他扰动参数的组合,表明就本次过程而言,随机扰动边界层方案中,去时间相关选择6 h,去空间尺度选择70 km可以获得较好的集合预报技巧。而对于SPPR试验,不同扰动参数对集合预报的技巧影响相对较小,这是由于该方案的总体扰动能量偏小造成的,相对而言,在随机扰动陆面方案中,去时间相关选择6 h,去空间尺度选择50 km可以获得较好的集合预报技巧。
(5) 混合使用随机扰动边界层和陆面过程参数方案(SPPM+SPPR),系统扰动能量的增加并不显著,混合扰动方案的模式变量的离散度演变与单独机扰动边界层方案类似。降水的检验表明,除6 h降水≥50 mm ETS评分混合扰动方案明显优于其他试验,其他评分结果与随机扰动边界层参数相当,这可能与RUC陆面过程方案参数方案的扰动能量太小有关。
为了探讨SPP方法扰动MYNN边界层方案和RUC陆面过程方案参数的特点及其相关扰动参数的设置,本研究只引入单一的扰动方案,因而集合预报系统的离散度总体偏小,但即便如此,两种不同物理过程随机扰动的集合平均均能获得比控制预报更好的预报效果,表明这两种随机方案对集合预报系统均具有正贡献。此外,扰动边界层方案比陆面过程能获得更大的扰动能量,可能与模式中边界层方案自身对降水的影响更大或者与天气过程的类型有关(李昀英等,2010;陈海山等,2014),这个也是一个值得进一步研究的课题。
通过一次典型西部山地暴雨个例的随机物理过程试验,得到较小的去空间相关系数(70 km/50 km)和较长的去时间相关系数(6 h),可以获得较优的集合预报技巧,即在对上述物理方案参数的随机扰动中,较小的扰动空间尺度和较低的扰动场随时间的变化频率,可以获得较优的集合预报技巧,上述结论还需要更多的试验予以验证。本文并没有对所有可能的时空参数进行对比试验,已有的一些研究表明,随机扰动的时空参数与天气过程相关,参数的选择应与天气系统的尺度相适应(闵锦忠等,2018),但任何一次天气过程都是不同尺度天气系统相互作用的结果,因此两者之间的确切关系,还需要做进一步的研究。此外,随机扰动时空尺度的选择与被扰动对象(物理过程)之间的关系,也是一个值得深入研究的课题,因此,在实际应用随机方案之前,非常有必要针对特定地域和预报对象,开展最优的扰动参数的试验。
蔡沅辰, 闵锦忠, 庄潇然, 2017. 不同随机物理扰动方案在一次暴雨集合预报中的对比研究[J]. 高原气象, 36(2): 407-423. Cai Y C, Min J Z, Zhuang X R, 2017. Comparison of different stochastic physics perturbation schemes on a storm-scale ensemble forecast in a heavy rain event[J]. Plateau Meteor, 36(2): 407-423 (in Chinese).
|
陈海山, 倪悦, 苏源, 2014. 两次暴雨过程模拟对陆面参数化方案的敏感性研究[J]. 气象学报, 72(1): 79-99. Chen H S, Ni Y, Su Y, 2014. Sensitivity of heavy rainfall events simulation to land surface parameterization scheme as simulated via the two cases[J]. Acta Meteor Sin, 72(1): 79-99 (in Chinese).
|
陈静, 薛纪善, 颜宏, 2003. 物理过程参数化方案对中尺度暴雨数值模拟影响的研究[J]. 气象学报, 61(2): 203-218. Chen J, Xue J S, Yan H, 2003. The impact of physics parameterization schemes on mesoscale heavy rainfall simulation[J]. Acta Meteor Sin, 61(2): 203-218 (in Chinese).
|
陈涛, 孙军, 谌芸, 等, 2019. 广州"5·7"局地突发特大暴雨过程的数值可预报性分析[J]. 气象, 45(9): 1199-1212. Chen T, Sun J, Chen Y, et al, 2019. Study on the numerical predictivity of localized severe mesoscale rainstorm in Guangzhou on 7 May 2017[J]. Meteor Mon, 45(9): 1199-1212 (in Chinese).
|
杜钧, 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28. Du J, 2002. Present situation and prospects of ensemble numerical prediction[J]. J Appl Meteor Sci, 13(1): 16-28 (in Chinese). DOI:10.3969/j.issn.1001-7313.2002.01.002
|
杜钧, 李俊, 2014. 集合预报方法在暴雨研究和预报中的应用[J]. 气象科技进展, 4(5): 6-20. Du J, Li J, 2014. Application of ensemble methodology to heavy-rain research and prediction[J]. Adv Meteor Sci Technol, 4(5): 6-20 (in Chinese).
|
Kalnay E, 2005. 大气模式、资料同化和可预报性[M]. 蒲朝霞, 译. 北京: 气象出版社. Kalnay E, 2005. Atmospheric Modeling, Date Assimilation and Predictability[M]. Pu Z X, trans. Beijing: China Meteorological Press(in Chinese).
|
李俊, 杜钧, 王明欢, 等, 2009. 中尺度暴雨集合预报系统研发中的初值扰动试验[J]. 高原气象, 28(6): 1365-1375. Li J, Du J, Wang M H, et al, 2009. Experiments of perturbing initial conditions in the development of mesoscale ensemble prediction system for heavy rainstorm forecasting[J]. Plateau Meteor, 28(6): 1365-1375 (in Chinese).
|
李俊, 杜钧, 刘羽, 2015. 北京"7·21"特大暴雨不同集合预报方案的对比试验[J]. 气象学报, 73(1): 50-71. Li J, Du J, Liu Y, 2015. A comparison of initial condition-, multi-physics- and stochastic physics-based ensembles in predicting Beijing "7·21" excessive storm rain event[J]. Acta Meteor Sin, 73(1): 50-71 (in Chinese).
|
李俊, 杜钧, 许建玉, 等, 2020. 一次特大暴雨过程高分辨率集合预报试验的检验和评估[J]. 暴雨灾害, 39(2): 176-184. Li J, Du J, Xu J Y, et al, 2020. The assessment and verification of high-resolution ensemble forecast for a heavy rainstorm[J]. Torr Rain Dis, 39(2): 176-184 (in Chinese). DOI:10.3969/j.issn.1004-9045.2020.02.008
|
李昀英, 叶成志, 钟中, 2010. 陆面参数化方案对两例不同类型暴雨可预报性的影响[J]. 大气科学, 34(2): 407-417. Li Y Y, Ye C Z, Zhong Z, 2010. Impacts of land-surface process parameterization on model predictability of two kinds of heavy rainfall events[J]. Chin J Atmos Sci, 34(2): 407-417 (in Chinese). DOI:10.3878/j.issn.1006-9895.2010.02.14
|
闵锦忠, 刘畅, 王世璋, 等, 2018. 随机物理倾向扰动在风暴尺度集合预报中的影响研究[J]. 气象学报, 76(4): 590-604. Min J Z, Liu C, Wang S Z, et al, 2018. Impact of stochastically perturbed parameterization tendencies on storm-scale ensemble forecast[J]. Acta Meteor Sin, 76(4): 590-604 (in Chinese).
|
倪悦, 2013. 陆面过程对两类暴雨的可能影响研究[D]. 南京: 南京信息工程大学. Ni Y, 2013. Possibleimpacts of land-surface process on two kinds of heavy rainfall events[D]. Nanjing: Nanjing University of Information Science and Technology(in Chinese).
|
沈艳, 潘旸, 宇婧婧, 等, 2013. 中国区域小时降水量融合产品的质量评估[J]. 大气科学学报, 36(1): 37-46. Shen Y, Pan Y, Yu J J, et al, 2013. Quality assessment of hourly merged precipitation product over China[J]. Trans Atmos Sci, 36(1): 37-46 (in Chinese). DOI:10.3969/j.issn.1674-7097.2013.01.005
|
谭燕, 陈德辉, 2007. 基于非静力模式物理扰动的中尺度集合预报试验[J]. 应用气象学报, 18(3): 396-406. Tan Y, Chen D H, 2007. Meso-scale ensemble forecasts on physical perturbation using a non-hydrostatic model[J]. J Appl Meteor Sci, 18(3): 396-406 (in Chinese). DOI:10.3969/j.issn.1001-7313.2007.03.017
|
王璐, 沈学顺, 2019. 对流尺度集合预报与模式不确定性研究进展[J]. 气象, 45(8): 1158-1168. Wang L, Shen X S, 2019. Review on the representation of model uncertainty in convection-allowing ensemble prediction system[J]. Meteor Mon, 45(8): 1158-1168 (in Chinese).
|
王璐璐, 闵锦忠, 刘畅, 2020. 基于WRF模式的对流尺度边界层方案参数随机扰动方法研究[J]. 气象学报, 78(4): 636-647. Wang L L, Min J Z, Liu C, 2020. A study on stochastic perturbed planetary boundary layer scheme parameters at convective scale based on WRF model[J]. Acta Meteor Sin, 78(4): 636-647 (in Chinese).
|
徐桂荣, 崔春光, 周志敏, 等, 2014. 利用探空资料估算青藏高原及下游地区大气边界层高度[J]. 暴雨灾害, 33(3): 217-227. Xu G R, Cui C G, Zhou Z M, et al, 2014. Atmospheric boundary layer heights estimated from radiosonde observations over the Qing-hai-Tibet Plateau and its downstream area[J]. Torr Rain Dis, 33(3): 217-227 (in Chinese). DOI:10.3969/j.issn.1004-9045.2014.03.004
|
杨学胜, 2001. 业务集合预报系统的现状及展望[J]. 气象, 27(6): 3-9. Yang X S, 2001. The new development and the outlook of the operational ensemble prediction system[J]. Meteor Mon, 27(6): 3-9 (in Chinese).
|
袁月, 李晓莉, 陈静, 等, 2016. GRAPES区域集合预报系统模式不确定性的随机扰动技术研究[J]. 气象, 42(10): 1161-1175. Yuan Y, Li X L, Chen J, et al, 2016. Stochastic parameterization toward model uncertainty for the GRAPES mesoscale ensemble prediction system[J]. Meteor Mon, 42(10): 1161-1175 (in Chinese). DOI:10.7519/j.issn.1000-0526.2016.10.001
|
张涵斌, 范水勇, 陈敏, 等, 2019. 区域集合预报基于SKEB和多物理过程的混合模式扰动方法研究[J]. 气象, 45(1): 17-28. Zhang H B, Fan S Y, Chen M, et al, 2019. Study on a synthetic model perturbation method based on SKEB and multi-physics for regional ensemble forecast[J]. Meteor Mon, 45(1): 17-28 (in Chinese).
|
赵滨, 张博, 2018. 邻域空间检验方法在降水评估中的应用[J]. 暴雨灾害, 37(1): 1-7. Zhao B, Zhang B, 2018. Application of neighborhood spatial verification method on precipitation evaluation[J]. Torr Rain Dis, 37(1): 1-7 (in Chinese). DOI:10.3969/j.issn.1004-9045.2018.01.001
|
智协飞, 董甫, 张玲, 等, 2020. 基于不同微物理过程的广西沿海南风型暖区暴雨的数值模拟研究[J]. 大气科学学报, 43(5): 867-879. Zhi X F, Dong F, Zhang L, et al, 2020. Numerical simulation of southerly type warm-sector heavy rainfall in the coastal region of Guangxi using various cloud microphysics parameterization schemes in the WRF model[J]. Trans Atmos Sci, 43(5): 867-879 (in Chinese).
|
周文艳, 罗勇, 史学丽, 等, 2019. 陆面过程模式BCC_AVIM中地表覆盖数据现状[J]. 气象, 45(10): 1476-1482. Zhou W Y, Luo Y, Shi X L, et al, 2019. Status of land cover datasets for the BCC_AVIW land surface model[J]. Meteor Mon, 45(10): 1476-1482 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.10.014
|
Baker L H, Rudd A C, Migliorini S, et al, 2014. Representation of model error in a convective-scale ensemble prediction system[J]. Nonlinear Process Geophys, 21(1): 19-39. DOI:10.5194/npg-21-19-2014
|
Berner J, Ha S Y, Hacker J P, et al, 2011. Model uncertainty in a mesoscale ensemble prediction system: stochastic versus multiphysics representations[J]. Mon Wea Rev, 139(6): 1972-1995. DOI:10.1175/2010MWR3595.1
|
Berner J, Shutts G J, Leutbecher M, et al, 2009. A spectral stochastic kinetic energy backscatter scheme and its impact on flow-dependent predictability in the ECMWF ensemble prediction system[J]. J Atmos Sci, 66(3): 603-626. DOI:10.1175/2008JAS2677.1
|
Bowler N E, Arribas A, Mylne K R, et al, 2008. The MOGREPS short-range ensemble prediction system[J]. Quart J Roy Meteor Soc, 134(632): 703-722. DOI:10.1002/qj.234
|
Huang Y, Peng X D, 2017. Improvement of the Mellor-Yamada-Nakanishi-niino planetary boundary-layer scheme based on observational data in China[J]. Bound-Layer Meteor, 162(1): 1-18. DOI:10.1007/s10546-016-0191-4
|
Jankov I, Berner J, Beck J, et al, 2017. A performance comparison between multiphysics and stochastic approaches within a North American RAP ensemble[J]. Mon Wea Rev, 145(4): 1161-1179. DOI:10.1175/MWR-D-16-0160.1
|
Leutbecher M, Lock S J, Ollinaho P, et al, 2017. Stochastic representations of model uncertainties at ECMWF: state of the art and future vision[J]. Quart J Roy Meteor Soc, 143(707): 2315-2339. DOI:10.1002/qj.3094
|
Mellor G L, Yamada T, 1974. A hierarchy of turbulence closure models for planetary boundary layers[J]. J Atmos Sci, 31(7): 1791-1806. DOI:10.1175/1520-0469(1974)031<1791:AHOTCM>2.0.CO;2
|
Nakanish M, 2001. Improvement of the Mellor-Yamada turbulence closure model based on large-eddy simulation data[J]. Bound-Layer Meteor, 99(3): 349-378. DOI:10.1023/A:1018915827400
|
Nakanishi M, Niino H, 2006. An improved Mellor-Yamada level-3 model: its numerical stability and application to a regional prediction of advection fog[J]. Bound-Layer Meteor, 119(2): 397-407. DOI:10.1007/s10546-005-9030-8
|
Ollinaho P, Lock S J, Leutbecher M, et al, 2017. Towards process-level representation of model uncertainties: stochastically perturbed parametrizations in the ECMWF ensemble[J]. Quart J Roy Meteor Soc, 143(702): 408-422. DOI:10.1002/qj.2931
|
Palmer TN, 2012. Towards the probabilistic earth-system simulator: A vision for the future of climateand weather prediction[J]. Quart J Roy Meteor Soc, 138(665): 841-861. DOI:10.1002/qj.1923
|
Palmer T N, Buizza R, Doblas-Reyes F, et al, 2009. Stochastic parametrization and model uncertainty[R]. England: ECMWF Technical Memorandum: 42.
|
Roberts N M, Lean H W, 2008. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events[J]. Mon Wea Rev, 136(1): 78-97. DOI:10.1175/2007MWR2123.1
|
Shutts G, 2005. A kinetic energy backscatter algorithm for use in ensemble prediction systems[J]. Quart J Roy Meteor Soc, 131(612): 3079-3102. DOI:10.1256/qj.04.106
|
Skamarock W C, Klemp J B, Dudhia J, et al, 2005. A description of the advanced research WRF Version 2[R]. NCAR Tech Note, 468+STR. Boulder: NCAR: 125.
|
Smirnova T G, Brown J M, Benjamin S G, et al, 2000. Parameterization of cold-season processes in the MAPS land-surface scheme[J]. J Geophys Res Atmos, 105(D3): 4077-4086. DOI:10.1029/1999JD901047
|
Stull R B. 1988. An Introduction to Boundary Layer Meteorology[M]. Dordrecht: Springer.
|
Weaver A, Courtier P, 2001. Correlation modelling on the sphere using a generalized diffusion equation[J]. Quart J Roy Meteor Soc, 127(575): 1815-1846. DOI:10.1002/qj.49712757518
|
 2021, Vol. 47
2021, Vol. 47 
