2. 国防科技大学气象海洋学院, 长沙 410005
2. College of Meteorology and Oceanology, National University of Defense Technology, Changsha 410005
降水与人类生产生活息息相关,定量测量降水(QPE)一直是气象和水文领域的焦点。天气雷达是区域降水监测的有效手段,其利用降水估计关系(PE)即观测量与降水的关系进行定量测量降水,如常用的雨强R与反射率因子Z间的Marshall-Palmer关系Z=200R1.6(Marshall et al,1955)、“雷暴”关系Z=300R1.4(Fulton et al,1998)等。近年来,利用无线微波链路(ML)实施降水监测受到广泛关注,ML能够通过测量路径累积衰减,使用衰减系数与降水强度的关系(雨衰关系)测量降水(姜世泰等,2013),利用雨衰关系反演降水更具鲁棒性,而且ML分布广泛,具有无需额外投入的突出优势(Messer et al,2006)。
微波链路雨衰关系和雷达PE关系的准确性是微波链路和雷达QPE的关键。然而雨滴谱的时空变化导致雨衰关系和PE关系也存在时空变化,不同地区、季节、类型降水中的雨衰关系和PE关系存在较大差异(Wilson and Brandes, 1979)。Battan(1973)曾根据气候条件给出过69种不同的Z-R关系。国际电信联盟(ITU)建议的ITU-R模型得到广泛使用,但一些局地的雨衰试验结果与ITU-R模型结果差异较大,充分说明雨衰模型参数需要根据地域、气候、滴谱特征进行调整(Baldotra and Hudiara, 2004;van Leth et al,2018)。
近年来,随着实测雨滴谱数据质量的提升,使用雨滴谱数据分析降水特性的研究取得了较好效果。黄兴友等(2019)使用Parsivel激光雨滴谱仪获取了32次降雨过程的雨滴谱资料,拟合了雷达反射率因子与降雨强度间的关系,利用衰减参数进行了雷达回波衰减订正试验。沙修竹等(2019)、李力等(2018)对比分析了雨滴谱反演降水强度与雨量计观测降水强度的差异。Mineo et al(2019)利用雨滴谱数据分析验证了降雨动能与雨强间的关系。濮江平等(2010)利用雨滴谱数据,分析对比了南京地区不同云系降水中雨滴谱分布特征的差异。这些研究都体现出实测滴谱数据在降水特性分析中的有效性。
因此,为得到更为准确的雨衰特性和雷达PE关系,本文利用实测雨滴谱数据,统计了南京地区不同类型降水滴谱特征,对微波雨衰关系和天气雷达降水估计关系进行了计算,并在实际降水过程中进行分析验证,从而为定量测量降水等相关研究提供参考。
1 雨滴谱数据使用南京地区连续两年夏季的实测雨滴谱数据,包括2014年5月1日至7月31日南京江宁区站点的雨滴谱数据,以及2015年5月1日至7月31日南京浦口区站点的雨滴谱数据。
1.1 测量方法所用雨滴谱数据由德国OTT公司的Parsivel激光降水粒子谱仪获取。Parsivel雨滴谱仪(Löffler-Mang and Joss, 2000)采用平行激光束进行采样,以光电管阵列为接收传感器,当有降水粒子穿越采样空间时,遮挡物的宽度和穿越时间被仪器自动记录,由此可计算降水粒子的尺度分布和速度。仪器测量的数据共有32个尺度测量通道和32个速度测量通道,其中粒子尺度测量数据范围为0.2~25 mm,粒子速度测量数据范围为0.2~20 m·s-1。仪器的采样间隔可设为10 s~2 h,每个采样间隔内的粒子谱测量数据都有32×32=1 024个。滴谱仪连续采样,采样时间设定为1 min,采样面积为0.005 4 m2。
1.2 质量控制首先对雨滴谱数据进行质量控制,对雨强 < 0.5 mm·h-1且粒子数少于10个的样本,认为其是无降水或仪器噪声所致,删除;认为偏离Atlas经验曲线(Atlas et al,1973) 50%的数据为异常值,进行剔除。由于观测到的对流性降水雨滴最大尺度接近6 mm(濮江平等,2010),所以剔除直径大于6 mm的雨滴数据。经过上述处理,最终得到14 153个有效数据样本(每分钟一个样本)。
由于Parsivel激光降水粒子谱仪发射的激光是在水平方向上进行雨滴尺度测量,观测到的雨滴直径通常为椭球型雨滴的长轴直径,导致测量值偏大,所以采用Battaglia et al(2010)的方法对观测数据进行雨滴形变修正,方法如下:
| $ D_{q}=\left\{\begin{array}{lc} D_{\text {mea }} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ D_{\operatorname{mea}} \leqslant 1 \mathrm{~mm} \\ \left(1.075-0.075 D_{\text {mea }}\right) D_{\text {mea }} \\ \ \ \ \ \ \ \ 1 \mathrm{~mm}<D_{\mathrm{mea}} \leqslant 5 \mathrm{~mm} \\ 0.7 D_{\mathrm{mea}} \ \ \ \ \ \ \ \ \ \ D_{\mathrm{mea}}>5 \mathrm{~mm} \end{array}\right. $ | (1) |
式中:Dq为雨滴等效球形直径,Dmea为Parsivel实测雨滴直径。
1.3 样本统计根据雨滴谱数据,可采用阶矩法计算相关降水物理量,将第i阶矩量定义为:
| $ M_{i}=\int_{0}^{\infty} D^{i} N(D) \mathrm{d} D $ | (2) |
式中:M的下标表示阶数,D为雨滴直径,N(D)为直径为D的雨滴数。降水粒子数密度n、雨强R、雷达反射率因子Z分别对应0、3、6阶矩量:
| $ n=\int_{0}^{\infty} N(D) \mathrm{d} D $ | (3) |
| $ R=\frac{\pi}{6} \int_{0}^{\infty} D^{3} N(D) V(D) \mathrm{d} D $ | (4) |
| $ Z=\int_{0}^{\infty} D^{6} N(D) \mathrm{d} D $ | (5) |
根据Atlas and Ulbrich(1977)的研究,雨滴降落末速:
| $ V(D)=3.778 D^{0.67} $ | (6) |
基于实际雨滴谱数据,利用式(5),可得粒子数和雷达反射率因子,将式(6)代入式(4),即可计算雨强值。将以下标准作为降水分类规则(Chen et al,2013):
(1) 连续10 min内,平均雨强>0.5 mm·h-1,标准差 < 1.5 mm·h-1为层状云降水;
(2) 平均雨强>5 mm·h-1,标准差>1.5 mm·h-1为对流性降水;
(3) 除以上两类之外,即0.5 mm·h-1 < 平均雨强 < 5 mm·h-1,标准差>1.5 mm·h-1,或平均雨强>5 mm·h-1,标准差 < 1.5 mm·h-1的降水样本,即弱雨高标准差或强雨低标准差,归为其他类型降水, 主要应为弱对流性降水和混合性降水。
按照以上标准,在14 153个有效滴谱样本中判别出7 278个层状云降水样本、4 136个对流性降水样本、2 739个其他类型降水样本,各类型样本数量分布如表 1所示。
|
|
表 1 雨滴谱数据的降水类型分布(单位:min) Table 1 The precipitation type distribution of DSD data (unit: min) |
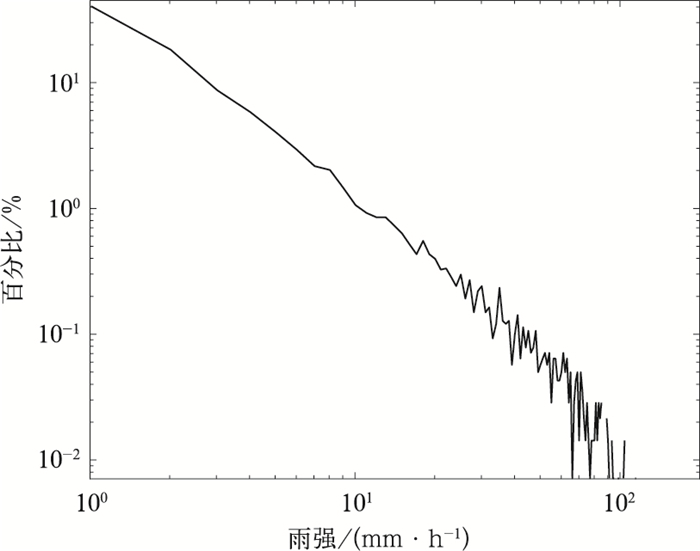
从表 1中可以看到,2015年5—7月浦口地区降水时次多于2014年5—7月江宁地区的降水时次,相比于层状云和其他型降水,对流性降水时次增加量略大。不同雨强对应的样本数量比例如图 1所示。
|
图 1 雨滴谱数据的雨强分布 Fig. 1 The rain rate distribution of DSD data |
由图 1可见,绝大部分降水集中在10 mm·h-1以下,整体上,降水样本数随雨强增大而迅速减小,在雨强>12 mm·h-1后开始出现震荡,且雨强越大,波动越强。其中低于5 mm·h-1的降水样本占比为77.88%,高于20 mm·h-1的降水样本占比为6.17%,雨强整体高于张洪胜等(2017)对2010—2014年南京地区全年滴谱数据的统计结果,而与Chen et al(2013)统计的梅雨锋降水中雨强分布相似。
各降水类型的统计量见表 2,可见所有类型降水标准差(10.95 mm·h-1)与雨强均值(5.11 mm·h-1)的比值为2.14,与Sauvageot(1994)发现的陆地降水中雨强标准差与平均值之间的比值(约为2.24)的结论非常相近。
|
|
表 2 各类型降水统计量 Table 2 Statistics of all types of precipitation |
根据微波传输理论,路径微波衰减系数γrain(dB/km)可表示成为如下形式(姜世泰等,2013):
| $ \gamma_{\mathrm{rain}}=0.434 \int_{D_{\min }}^{D_{\max }} C_{\text {ext }, f} \cdot \bar{N}\left(D_{\mathrm{e}}\right) \mathrm{d} D_{\mathrm{e}} $ | (7) |
式中:De是雨滴的等效直径,N(De)为路径的平均雨滴谱分布,Cext,f为微波偏振频率f时的雨滴消光截面。可见,在获得雨滴谱分布后,计算微波雨衰的关键在于计算雨滴消光截面,而消光截面是粒子对电磁波衰减能力的度量,其大小与粒子尺度、形状、环境温度、微波频率和偏振状态有关。目前计算粒子消光截面的方法较多,有Mie散射理论、T矩阵理论等,研究表明使用T矩阵理论计算非球形粒子的散射衰减特性精度较高(徐飞等,2005)。因此本文采用T矩阵理论计算不同波长的雨滴衰减截面,计算方法详见Waterman(1969)。由于雨滴的复折射指数与温度有关,因此需要考虑温度的影响。根据温度对衰减的影响的相关研究(刘西川等,2018),发现在-20℃~30℃范围内,温度对雨滴衰减的影响可近似忽略,因此本文将20℃作为T矩阵计算的输入参数。
2.2 ITU-R雨衰模型国际电信联盟(ITU)建议的ITU-R模型,适用于55 GHz频率以下的微波雨致衰减预测。该模型中衰减系数γrain(dB/km)与雨强R(mm·h-1)为幂律关系:
| $ \gamma_{\text {rain }}=k R^{\alpha} $ | (8) |
ITU-R建议书还给出了线极化和水平链路条件下,随频率变化的系数k和α在部分整数频点的取值,其他频点下的系数取值可采用插值方法(k采用对数插值,α采用线性插值)。
2.3 实测雨衰特性分析使用非线性拟合方法,根据实测雨滴谱数据拟合雨致衰减与雨强的幂律关系(式8),得到系数k和α随频率的取值分布,并与ITU-R雨衰模型建议的参数取值进行比较,垂直偏振条件下各种降水型雨衰关系的系数对比结果如图 2所示。

|
图 2 垂直偏振条件下各种降水型的雨衰关系系数k(a,c,e,g)和α(b,d,f,h)分布 (a,b)全部类型降水,(c,d)层状云降水,(e,f)对流性降水,(g,h)其他型降水 Fig. 2 The parameters k (a, c, e, g) and α (b, d, f, h) of rain-attenuation relationship of different precipitation types under vertical polarization condition (a, b) all type precipitation, (c, d) convective precipitation, (e, f) stratiform precipitation, (g, h) other type precipitation |
由图 2可见,由于ITU-R雨衰模型为达到一定的应用普适性,对雨滴谱分布特征和粒子散射特性进行了一定简化和假设,导致ITU-R雨衰模型建议的参数取值(k和α)与实测雨滴谱数据拟合得到的雨衰模型系数并不相同,其中系数k的差异相对较小,在层状云降水和其他类型降水时,实测数据拟合得到的系数k小于ITU-R建议的k值,差异随频率增加而增加。而在对流性降水中,实测数据拟合的k值先低于ITU-R建议值,在9 GHz之后高于ITU-R建议值,总体上差异小于层状云降水和其他类型降水。相比于系数k,系数α的差异较大,在层状云降水和其他类型降水中,实测数据拟合的系数α值先低于ITU-R建议取值,在6 GHz和9 GHz之后高于ITU-R建议取值。对流性降水中的α值差异也很大,实测数据拟合的系数α值先高于ITU-R建议取值,在11 GHz之后低于ITU-R建议取值,在6 GHz处差异最大。所有降水样本数据拟合的系数值与对流性降水相似。
由于实测数据拟合得到的雨衰模型系数与ITU-R建议值不同,所以使用ITU-R雨衰模型由衰减系数反算降水强度必然存在误差,图 3显示了在微波频率为8 GHz、垂直极化条件下,分别使用实测数据拟合的雨衰模型和ITU-R雨衰模型,由衰减系数反算雨强的结果。

|
图 3 实测滴谱拟合雨衰模型与ITU-R模型反演降水对比 (a)全部类型降水,(b)层状云降水,(c)对流性降水,(d)其他类型降水 Fig. 3 Comparison of rain rates derived by rain-attenuation model fitted by measured DSD data and ITU-R model (a) all type precipitation, (b) stratiform precipitation, (c) convective precipitation, (d) other type precipitation |
显然,使用ITU-R雨衰模型和实测数据拟合的雨衰模型,由衰减系数反算雨强的结果存在差异。微波垂直极化与水平极化条件下,雨强反演偏差分布基本相同。具体地说,层状云降水条件下,ITU-R反演结果高估雨强,除层状云降水之外的其他降水类型条件下低估,所有类型降水中总体表现为低估雨强。ITU-R反演雨强的偏差随雨强增大而增大,高估层状云降水与低估对流性降水的偏差大致相同,而低估其他类型降水的偏差最大。因此,使用ITU-R雨衰模型将带来较大误差,必须使用本地化的雨衰模型,才能获得较高的降水反演准确度。
3 天气雷达降水估计关系分析雷达反射率因子Z和雨强R,二者之间存在如下关系:
| $ Z=a R^{b} $ | (9) |
转换为dB单位,即两边取对数可得:
| $ d B z=b \cdot d B R+10 \lg a $ | (10) |
式中: dBz=10lgZ,dBR=10lgR。转换为dB单位后,dBz与dBR呈线性关系,可用线性拟合得到系数a、b的值。实测滴谱数据拟合结果如图 4所示。

|
图 4 同图 3,但为实测滴谱拟合的Z-R关系 Fig. 4 Same as Fig. 3, but for Z-R relationship fitted with measured DSD data |
可见,实测滴谱数据拟合得到的Z-R关系与常用层状云降水关系Z=200R1.6(Marshall et al,1955)或对流云降水关系Z=300R1.4(Fulton et al,1998)均有差异,使用默认降水估测关系根据雷达反射率因子计算雨强将导致误差。
4 试验与分析在实际降水过程中应用和检验了基于实测滴谱数据拟合的雨衰关系和PE关系。
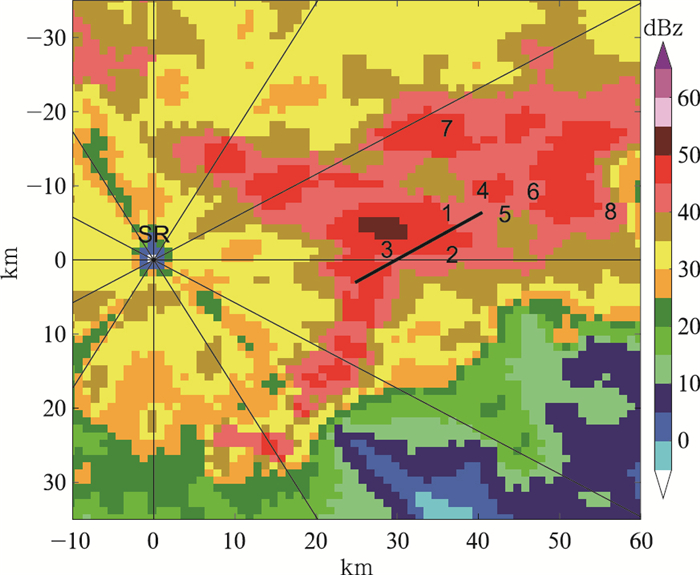
4.1 实验设备使用1部S波段天气雷达、1条微波链路和8个雨量计进行试验分析,各设备相对位置如图 5所示。微波链路长为24.05 km,发射频率为7.7 GHz,垂直极化。相对于S波段天气雷达,微波链路发射端处在径向距离为25 km、方位97°处,接收端处在距离41 km、方位81°处,共对应S波段雷达17个距离库。
|
图 5 2016年6月1日S波段天气雷达0.5°仰角PPI强度回波 (SR:S波段天气雷达,黑线:微波链路,数字:雨量计) Fig. 5 Reflectivity PPI at elevation 0.5° of the S-band radar on 1 June 2016 (SR: S-band radar, black line: mircowave link, number: rain gauge) |
该微波链路为业务用通信链路,接收端实时记录接收功率,精确到0.1 dB。为得到链路路径衰减,首先应确定微波链路的基准电平,即链路路径无降水时的接收功率。在本文试验中,将距离微波链路最近的雨量计1和雨量计2作为干/湿指示器,当任一雨量计显示某时刻有降水,即认定该时刻为降水时刻,基准电平为最后“干”时刻的接收功率。则链路路径总衰减量可以通过比较接收功率和基准电平而得到,进而由总衰减量除以链路长度得到链路路径平均衰减系数。
为分析微波链路反演降水的效果,选择离链路较近(距离链路中点距离 < 20 km)的8个雨量计,图 5中数字顺序即为各雨量计距链路中心点的距离排序(由近及远)。8个雨量计相对S波段雷达的距离和方位以及与链路中点的距离见表 3。
|
|
表 3 雨量计相对于雷达和链路的位置 Table 3 Positions of rain gauges relative to the radar and the microwave link |
2016年6月1日,南京地区发生了一次暴雨过程,降水从08—13时持续5 h,以雷达完成一个体积扫描的时间(6 min)为1个时次,此次降水持续了50个时次,降水由强转弱。第9时次的S波段雷达强度回波如图 5所示。该时次回波分布不均匀,回波边缘清晰,强中心强度强,最大强度达到55 dBz,雨量计测量的最大雨强达到了70 mm·h-1。综合分析各时次多仰角回波图像和雨量计实测雨量,可以判断此次降水过程的前14个时次主要为对流性降水,之后转变为层状云弱降水为主。
4.2.2 微波链路反演降水由于此次降水过程为对流性降水转为层状云弱降水为主,因此,对于微波链路反演雨强,本次降水过程的前14个时次,使用根据雨滴谱计算得到的7.7 GHz垂直极化条件下的对流性降水雨衰模型:
| $ \gamma_{\mathrm{rain}}=0.000\ 5 R_{\mathrm{ML}}{}^{1.693\ 8} $ | (11) |
式中:γrain和RML分别为微波链路平均衰减系数和平均降水强度。对之后的36个匹配时次,使用由雨滴谱统计得到的层状云降水雨衰模型:
| $ \gamma_{\mathrm{rain}}=0.002\ 5 R_{\mathrm{ML}}{}^{1.526\ 5} $ | (12) |
同时使用ITU-R雨衰关系反演降水,在电磁波垂直极化、频率为7.7 GHz条件下,ITU-R雨衰关系为:
| $ \gamma_{\text {rain }}=0.003\ 95 R_{\mathrm{ML}}{}^{1.31} $ | (13) |
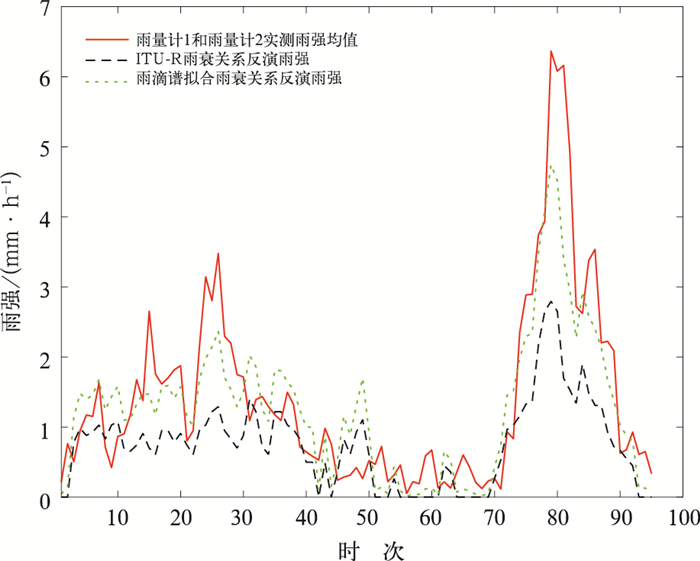
图 6显示了微波链路反演降水与距离链路最近的雨量计1和雨量计2实测降水的对比。

|
图 6 微波链路反演降水与雨量计实测降水的对比(降水过程Ⅰ) Fig. 6 Comparison of the rain rates in precipitation Case Ⅰ derived by microwave link and rain gauge |
绘制微波链路反演降水与雨量计1和雨量计2实测降水的散点(图 7)。
|
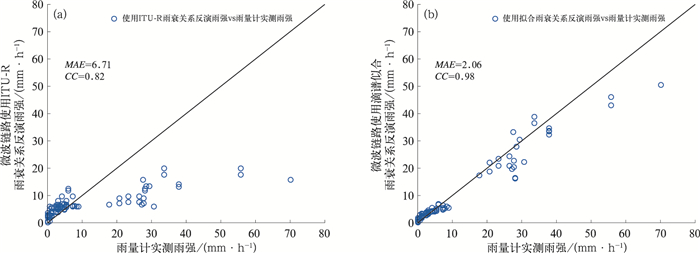
图 7 雨量计实测雨强与微波链路使用(a)ITU-R雨衰关系和(b)滴谱拟合雨衰关系反演雨强的散点(降水过程Ⅰ) Fig. 7 Scatter plots of the rain rates measured in precipitation Case Ⅰ by rain gauges against those derived by microwave link using (a) ITU-R model and (b) rain-attenuation relationship fitted with DSD data |
由图 7可见,使用ITU-R雨衰关系反演雨强存在着低估对流性降水而高估层状云降水的问题,特别是在较强对流性降水时严重低估。而使用雨滴谱拟合雨衰关系反演的雨强与雨量计实测雨强更加接近,平均绝对误差(MAE)降至2.06,相关系数(CC)提高至0.98,低估对流性降水和高估层状云降水的问题得到较大改善。值得注意的是,此次降水过程第15时次之后整体上以层状云降水为主,但在第35时次雨量计1位置处仍为弱对流性降水,导致了一定的反演误差。
4.2.3 雷达反演降水对于雷达反演降水,由于使用的是S波段雷达最低层(仰角0.5°)PPI反射率因子数据,所以在反演降水之前,首先进行非气象回波消除以及滤波处理,以减少非气象回波和噪声的影响。对于本次降水过程的前14个时次,使用对流性降水PE关系Z=161.63R1.55,之后的36个匹配时次,使用层状云降水PE关系Z=227.23R1.53。所得降水反演的与常用层状云PE关系的反演结果以及雨量计实测降水进行比较。图 8为使用常用PE关系、雨滴谱拟合PE关系反演的雨强与雨量计实测雨强的散点图。
|
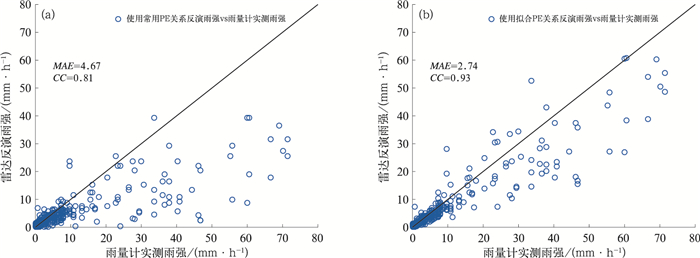
图 8 雨量计实测雨强与天气雷达使用(a)常用PE关系和(b)雨滴谱拟合PE关系反演雨强的散点 Fig. 8 Scatter plots of the rain rates measured by rain gauges against those estimated by the radar using (a) default PE relationship and (b) the PE relationship fitted with DSD data |
可见,使用常用层状云PE关系(Z=200R1.6)反演降水存在着低估降水的问题,特别是雨强较大时更为明显。而使用雨滴谱拟合PE关系反演的雨强与雨量计实测雨强更加接近,MAE降至2.74,CC提高至0.93,低估降水问题虽仍然存在,但已得到较大改善,充分表明使用滴谱拟合PE关系反演雨强较常用PE关系更为准确。
4.3 2016年6月12日降水过程Ⅱ 4.3.1 降水2016年6月12日南京地区的一次降水过程,分布范围广,持续时间长,从00时到接近10时共约10 h,将S波段天气雷达进行一次体积扫描的时间(6 min)作为1个时次,共对应于95个时次。整个降水过程整体呈现出混合性强降水特征,回波分布范围广,强度较强且分布不均匀,强中心明显。但校准区域处在整个降水区域的边缘位置,雷达回波强度相对较弱,分布很不均匀。从雨量计测值看,实测雨强较弱,通常低于10 mm·h-1,且随时间和位置的分布不均匀,降水在校准区域内各个时次均表现出这些特征,所以,校准区域内的降水主要为弱对流性降水。
4.3.2 微波链路反演降水由于本次降水过程为对流性弱降水,所以使用根据滴谱计算得到的7.7 GHz垂直极化条件下的其他类型降水雨衰模型(式14)以及ITU-R雨衰关系(式13),根据微波链路路径衰减反演降水。图 9显示了微波链路反演降水与雨量计1和雨量计2实测降水均值的对比。
| $ \gamma_{\text {rain }}=0.002\ 3 R_{\mathrm{ML}}{}^{1.304\ 4} $ | (14) |
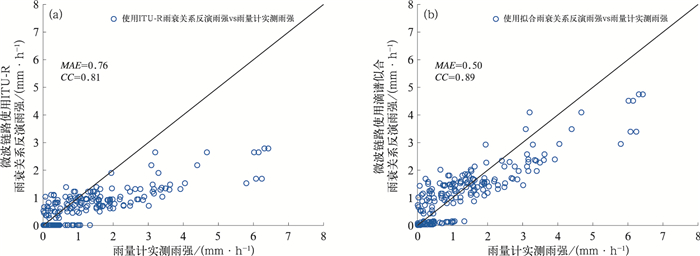
由图 9可见,微波链路反演的降水与雨量计实测降水随时间的变化趋势大体一致,但即便是在弱对流性降水中,微波链路使用ITU-R雨衰关系反演降水仍存在明显的低估问题。绘制微波链路反演降水与雨量计1和雨量计2实测降水均值的散点图(图 10)。
由图 10可见,使用滴谱拟合雨衰关系反演的雨强与雨量计实测雨强更加接近,MAE降至0.50,CC提高至0.89,低估弱对流性降水的问题得到改善。
5 结论与讨论本文统计分析了南京地区夏季实测雨滴谱数据,区分降水类型计算了雨衰关系和雷达降水估计关系,并在两次降水过程中进行了应用,与ITU-R雨衰关系和常用降水估计关系的降水反演结果进行了比较,得到以下结论:
(1) 雨滴谱数据拟合的雨衰关系与ITU-R建议模型存在差异,其中系数k的差异相对较小,系数α间的差异较大。对于层状云降水和其他类型降水(弱对流性降水和混合性降水),实测数据拟合得到的系数k小于ITU-R建议的k值,系数α值先低于后高于ITU-R建议值。而对于对流性降水,雨滴谱数据拟合的k值先低于后高于ITU-R建议值,雨滴谱数据拟合的系数α值先高于后低于ITU-R建议取值。
(2) 在一次强对流性降水转层状云降水的降水过程和一次弱对流性降水过程中,根据拟合得到的雨衰关系,使用微波链路得到的路径衰减进行了降水反演,并与ITU-R雨衰关系的反演结果和雨量计实测值进行了比较。结果表明,使用ITU-R雨衰关系反演降水存在高估层状云降水而低估对流性降水的问题,而使用滴谱拟合雨衰关系反演的雨强与雨量计实测雨强更加一致,平均绝对误差降低,相关性提高。
(3) 滴谱数据拟合的Z-R关系为:全部类型降水Z=221.24R1.45、层状云降水Z=227.23R1.53、对流性降水Z=161.63R1.55、其他类型降水Z=206.55R1.37,相比于常用的层状云降水Z=200R1.6关系,使用拟合PE关系反演降水与雨量计实测值更加接近。
黄兴友, 印佳楠, 马雷, 等, 2019. 南京地区雨滴谱参数的详细统计分析及其在天气雷达探测中的应用[J]. 大气科学, 43(3): 691-704. Huang X Y, Yin J N, Ma L, et al, 2019. Comprehensive statistical analysis of rain drop size distribution parameters and their application to weather radar measurement in Nanjing[J]. Chin J Atmos Sci, 43(3): 691-704 (in Chinese).
|
姜世泰, 高太长, 刘西川, 等, 2013. 基于微波链路的降雨场反演方法研究[J]. 物理学报, 62(15): 154303. Jiang S T, Gao T C, Liu X C, et al, 2013. Investigation of the inversion of rainfall field based on microwave links[J]. Acta Phys Sin, 62(15): 154303 (in Chinese). DOI:10.7498/aps.62.154303
|
李力, 姜有山, 蔡凝昊, 等, 2018. Parsivel降水粒子谱仪与观测站雨量计的对比分析[J]. 气象, 44(3): 434-441. Li L, Jiang Y S, Cai N H, et al, 2018. Contrastive analysis of parsivel precipitation particle spectrometer data and pluviometer data[J]. Meteor Mon, 44(3): 434-441 (in Chinese).
|
刘西川, 宋堃, 高太长, 等, 2018. 复杂大气条件对微波传播衰减的影响研究[J]. 电子与信息学报, 40(1): 181-188. Liu X C, Song K, Gao T C, et al, 2018. Research on the effect of complex atmospheric condition on microwave propagation attenuation[J]. J Electron Inf Technol, 40(1): 181-188 (in Chinese).
|
濮江平, 张伟, 姜爱军, 等, 2010. 利用激光降水粒子谱仪研究雨滴谱分布特性[J]. 气象科学, 30(5): 701-707. Pu J P, Zhang W, Jiang A J, et al, 2010. Characteristics of gamma raindrop size distribution based on the precipitation particle spectrometer[J]. Sci Meteor Sin, 30(5): 701-707 (in Chinese). DOI:10.3969/j.issn.1009-0827.2010.05.018
|
沙修竹, 丁建芳, 程博, 2019. 地面激光雨滴谱仪反演降水参量的特性探究[J]. 气象, 45(11): 1569-1578. Sha X Z, Ding J F, Cheng B, 2019. Characteristics of precipitation parameters reflected by ground laser rain drop disdrometer[J]. Meteor Mon, 45(11): 1569-1578 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.11.007
|
徐飞, 顾松山, 陈玉林, 2005. 用T矩阵方法计算超椭球粒子的电磁散射特性[J]. 南京气象学院学报, 28(6): 815-820. Xu F, Gu S S, Chen Y L, 2005. Computation of scattering features of hyper ellipsoids using the T-matrix method[J]. J Nanjing Inst Meteor, 28(6): 815-820 (in Chinese). DOI:10.3969/j.issn.1674-7097.2005.06.013
|
张洪胜, 何宏让, 张云, 等, 2017. 南京地区降水雨滴谱拟合模型的参数特征分析[J]. 气象与环境科学, 40(3): 71-78. Zhang H S, He H R, Zhang Y, et al, 2017. Parameter characteristic analysis of raindrop spectrum fitting models in Nanjing[J]. Meteor Environ Sci, 40(3): 71-78 (in Chinese).
|
Atlas D, Srivastava R C, Sekhon R S, 1973. Doppler radar characteristics of precipitation at vertical incidence[J]. Rev Geophys, 11(1): 1-35. DOI:10.1029/RG011i001p00001
|
Atlas D, Ulbrich C W, 1977. Path- and area-integrated rainfall measurement by microwave attenuation in the 1-3 cm band[J]. J Appl Meteor Climatol, 16(12): 1322-1331. DOI:10.1175/1520-0450(1977)016<1322:PAAIRM>2.0.CO;2
|
Baldotra A K, Hudiara I S, 2004. Rain attenuation statistics over terrestrial microwave link at 19.4 GHz at Amritsar[J]. IEEE Trans Antennas Propag, 52(6): 1505-1508. DOI:10.1109/TAP.2004.829852
|
Battaglia A, Rustemeier E, Tokay A, et al, 2010. Parsivel snow observations: a critical assessment[J]. J Atmos Ocean Technol, 27(2): 333-344. DOI:10.1175/2009JTECHA1332.1
|
Battan L J, 1973. Radar Observation of the Atmosphere[M].
Chicago: University of Chicago Press: 105-137.
|
Chen B J, Yang J, Pu J P, 2013. Statistical characteristics of raindrop size distribution in the Meiyu season observed in Eastern China[J]. J Meteor Soc Jpn, 91(2): 215-227. DOI:10.2151/jmsj.2013-208
|
Fulton R A, Breidenbach J P, Seo D J, et al, 1998. The WSR-88D rainfall algorithm[J]. Wea Forecasting, 13(2): 377-395. DOI:10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2
|
Löffler-Mang M, Joss J, 2000. An optical disdrometer for measuring size and velocity of hydrometeors[J]. J Atmos Ocean Technol, 17(2): 130-139. DOI:10.1175/1520-0426(2000)017<0130:AODFMS>2.0.CO;2
|
Marshall J S, Hitschfeld W, Gunn K L S, 1955. Advances in radar weather[J]. Adv Geophys, 2: 1-56.
|
Messer H, Zinevich A, Alpert P, 2006. Environmental monitoring by wireless communication networks[J]. Science, 312(5774): 713. DOI:10.1126/science.1120034
|
Mineo C, Ridolfi E, Moccia B, et al, 2019. Assessment of rainfall kinetic-energy-intensity relationships[J]. Water, 11(10): 1994. DOI:10.3390/w11101994
|
Sauvageot H, 1994. The probability density function of rain rate and the estimation of rainfall by area integrals[J]. J Appl Meteor Climatol, 33(4): 1255-1262.
|
van Leth T C, Overeem A, Uijlenhoet R, et al, 2018. A measurement campaign to assess sources of error in microwave link rainfall estimation[J]. Atmos Meas Tech, 11(8): 4645-4669. DOI:10.5194/amt-11-4645-2018
|
Waterman P C, 1969. New formulation of acoustic scattering[J]. J Acoust Soc Amer, 45(6): 1417-1429. DOI:10.1121/1.1911619
|
Wilson J W, Brandes E A, 1979. Radar measurement of rainfall-a summary[J]. Bull Amer Meteor Soc, 60(9): 1048-1060.
|
 2021, Vol. 47
2021, Vol. 47