引言

大气发射的下行长波辐射是全球辐射能量收支平衡中一个非常重要的成分，也是地表辐射模型中辐射预算的关键组成部分，准确计算大气下行长波辐射有利于了解影响地表能量平衡的因素(Zhu et al, 2017)。同时, 大气下行长波辐射研究在预报夜间霜冻、雾、温度变化、云量及改善区域天气预报、确定辐射冷却率、衡量气候变化和计算全球增暖等方面也发挥着重要作用(彭丽春等，2015)。

目前获得晴空下行长波辐射的方法主要有三种：地面气象站辐射计直接观测、根据复杂的大气辐射传输模型精确计算及通过经验公式计算获得。辐射计直接观测能方便准确地得到下行长波辐射值，但地面观测站点分布不均，因此大部分地区不具备直接观测的条件，目前只有部分国家气象观测站能获取相关数据(李伟斌等，2015)。在已知整层大气的垂直分布特性的条件下利用探空数据，通过复杂的大气辐射传输模型，可以获得下行长波辐射的理论值，然而由于探空数据不易获取，使用上述辐射传输模型计算时，常受到输入数据缺乏的限制(周允华，1984)。通过经验公式进行计算具有模型简单、观测数据(近地面气温、气压、水汽压等)易获得的优势，因此具有很强的实用性，在许多领域得到了广泛的应用(余珊珊等，2011；Alados et al, 2012)。例如Zhu et al(2017)在青藏高原地区对Brutsaert(1975)、Garratt(1992)、Prata(1996)和Swinbank(1963)等13个参数化方案进行了局地校正，获得了适用于该地区的参数化方案。近年来，下行长波辐射参数化研究取得了丰硕成果，例如Prata(1996)提出的参数化方案有效地改善了极端气候条件下的模拟精度，物理意义更加严谨，且适用性更强。Yu et al(2013)利用卫星热红外数据提出了具有高分辨率优势的参数化方案，后来又基于MODIS数据对该方案进行了改进，将模拟精度和适用性进一步提高(Yu et al, 2019)。Zhou et al(2019)利用中分辨率成像光谱仪数据及地面实测资料，基于多元自适应回归方法进行了晴空大气下行长波辐射计算，并在全球范围7个站点进行了验证。随着遥感科学的发展，气象观测的时空分辨率不断提高，下行长波辐射参数化方案模拟精度和适用性也得到了改善，但目前基于大气参数的参数化方案通常不具备广泛的适用性，尤其是在高海拔或干旱地区，通常存在较大的偏差，且误差会随着海拔的升高而增大，制约了参数化方案的适用性(Gubler et al, 2012)。

我国幅员辽阔，地形与气候条件较为复杂，利用上述参数化方案对晴空下行长波辐射进行理论计算的精确度难以满足要求。以青藏高原为例，由于其地处高寒地区，地面有效辐射和辐射平衡具有大致相同的量值，因此，下行长波辐射的精确估计对于高原地面辐射平衡和加热场的研究具有重要意义(周允华，1984；黄妙芬等，2005)。其次，入射长波辐射是青藏高原地区冰川融化的能量来源，利用准确的下行长波辐射值，有助于获得准确的模拟蒸散和冰川排放的结果，这对于冰川灾害预防、绿洲农业用水甚至西藏地区社会经济的整体发展都是必不可少的(Zhu et al, 2017；Ohmura, 2001；Sedlar and Hock, 2009)。此外，研究高寒地区晴空下行长波辐射对光能的利用具有指导性意义，可为新的清洁能源的开发提供积极广阔的前景。同时青藏高原对我国的气候变化有着重要的影响，精确地定量研究该地区的晴空下行长波辐射，对研究我国天气气候变化也有着重要意义。然而晴空下行长波辐射数据的缺乏，是能量平衡、气候模拟等研究常常面临的困难(余珊珊等，2011；闵敏和吴晓，2019)。

针对目前晴空大气下行长波辐射参数化方案在青藏高原及其他干旱地区适用性较差的问题，本研究基于Prata的参数化方案，考虑到入射到地面的长波辐射来自整层大气，对于不同海拔的地区来说，大气柱的高度不同，下行长波辐射值也不同，由此引进气压因素，根据ERA-5的再分析数据，通过多元函数拟合，获得了新形式的晴空大气发射率参数化方案，进而根据站点资料在全球不同海拔地区进行了模拟，与站点资料的下行长波辐射的观测值进行了对比，分析了新参数化方案在青藏高原及其他地区的适用性。

1 物理背景

入射到地面的大气下行长波辐射是其上整层大气发射的，与大气层温度和湿度的垂直分布、厚度密切相关，理论上可表示为垂直分层大气的积分形式。Steffan-Boltzman公式是近似计算长波辐射的常用公式，但该公式只适用于黑体，对于非黑体的大气来说，则需要考虑大气发射率。根据该公式，在晴空条件下，大气下行长波辐射计算公式可近似表示为：

$ L{W_{\rm{d}}} = {\varepsilon _{\rm{a}}}\sigma T_{\rm{a}}^4 $

(1)

式中: LW_d为晴空大气下行长波辐射，单位为W·m^-2；ε_a为晴空大气发射率；T_a通常取近地面大气温度代替整层大气的发射等效温度，单位为K；σ为玻尔兹曼常数，其值为5.67×10^-8 W·m^-2·K^-4。

由于晴空大气发射率无法通过直接测量获得，Brunt(1932)基于热传导与辐射传递之间的相似性，提出了晴空大气发射率与近地面水汽压相关的经验公式(Crawford and Duchon, 1999)：

$ {\varepsilon _{\rm{a}}} = a + b\sqrt e $

(2)

式中：e为近地面水汽压，单位为hPa；a、b为经验常数，a值约在0.34~0.66，b值约在0.033~0.127。由于经验常数因地区而异，给应用带来了不便。Swinbank(1963)指出下行长波辐射与水汽压之间并无关系，而仅仅与温度的平方有关，且Brunt(1932)经验公式有效的原因是水汽压与温度的正相关关系，进而提出了仅与近地面气温相关的经验公式(盛裴轩等，2013)：

$ {\varepsilon _{\rm{a}}} = aT_{\rm{a}}^2 $

(3)

式中：常数a=5.31×10^-14/σ; T_a为近地面气温，单位为K。

由于上式的常数不随地点而变，观测到的和估计的晴空大气下行长波辐射之间的相关系数为0.99，因而被广泛采用，但在高海拔地区，因水汽吸收的压力效应，需做高度校正(盛裴轩等，2013)。Brutsaert(1975)基于Schwarzschild方程和标准大气假设，提出了物理意义更严格的参数化方案：

$ {\varepsilon _{\rm{a}}} = a{\left({\frac{e}{{{T_{\rm{a}}}}}} \right)^b} $

(4)

从式中可以看出当水汽压为0时，该参数化方案得到的晴空大气发射率为0，但实际上，即使水汽含量为0，具有一定温度的大气同样能发射长波辐射，因此晴空大气发射率不应为0，故此结果并不能完全适用于计算晴空大气发射率。Prata(1996)指出，基于对单个气体吸收带的窄带模型和宽带模型的了解，可以用修正的指数带模型近似表示整个长波频谱，同时应考虑对水汽路径不均匀性加以修正，据此将辐射传输过程进行了高度简化近似，考虑了温度、湿度的垂直影响，引入了大气可降水量，提出了以下形式的参数化方案：

$ {\varepsilon _{\rm{a}}} = 1 - (1 + w){{\rm{e}}^{\left[ { - {{\left({{a_1} + {a_2}w} \right)}^m}} \right]}} $

(5)

式中：a₁，a₂和m是经验常数，a₁和a₂通过最小二乘拟合的方法获得，分别取1.2和3.0，m取1/2。w是大气可降水量，单位为g·cm^-2，可以根据以下方式进行计算：

$ w = c\frac{e}{{{T_{\rm{a}}}}} $

(6)

式中：c是一个常数，标准大气压假设下其取值为46.5。该参数化方案具有以下良好特性：当大气可降水量趋近于0，即大气接近为干空气时，只要具有一定温度，大气依然发出下行长波辐射，此时晴空大气发射率是一个常数，且该参数化方案估算的晴空大气发射率不会超过黑体的发射率。需要说明，随着海拔高度的升高，此参数化方案结果与观测值的均方根误差会增大，例如在海拔为3 580 m时，均方根误差达到长波辐射值的15%(Prata，1996)。鉴于此，本研究认为大气柱的厚度会对大气发射率产生影响，而长波辐射参数化方案在高寒地区的应用有望结合气压加以改进。

2 引入气压的参数化方案

由于Prata参数化方案具有干空气条件下，下行长波辐射依然存在和晴空大气发射率不超过黑体发射率的优点，本研究在Prata参数化方案的基础上，引入了气压因素，提出了以下三种形式的晴空大气发射率的参数化计算方案：

$ {\varepsilon \approx 1 - (1 + w)(1 + \zeta){{\rm{e}}^{ - {{(aw + b\zeta)}^c}}}} $

(7)

$ {\varepsilon \approx 1 - (1 + w)(1 + \zeta){{\rm{e}}^{ - {{\left[ {a{w^b} + c{\zeta ^d} + f{{(u\zeta)}^g}} \right]}^c}}}} $

(8)

$ {\varepsilon \approx 1 - {{\rm{e}}^{ - {{\left[ {a{w^b} + c{\zeta ^d} + f{{(u\zeta)}^g}} \right]}^c}}}} $

(9)

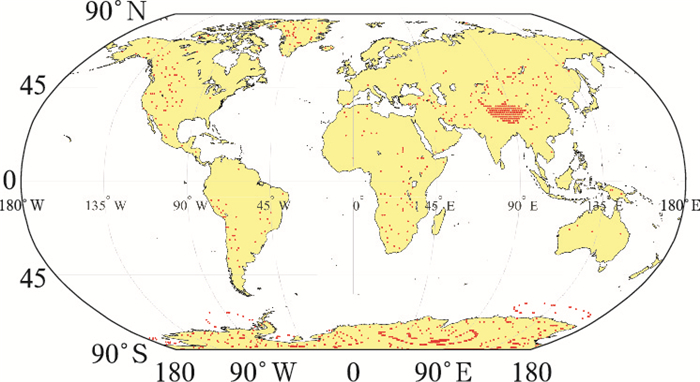
式中：ζ=p/p₀，p为当地大气压，p₀为标准大气压，w是大气可降水量，a、b、c、d、f、g均为经验常数。这里分别称式(7)~式(9)为方案1、方案2和方案3，上述三种方案中当气压趋近于0时，大气可降水量w趋近于0，则此时晴空大气发射率也趋近于0，且引入气压项后，晴空大气发射率依然不会超过黑体发射率。三种方案均保留了Prata方案在极限条件下的优良特性，但表达形式不同，大气发射率模拟结果也不相同。方案1参照了Prata进行水汽改正时的方法，在指数部分和系数部分同时添加气压项，方案2和方案3在方案1的基础上考虑了可降水量与气压的交互影响，因此理论上极限情况下表现更好。以上三种参数化方案中的经验常数通过使用2018年每月1日ERA-5全球再分析数据进行最小二乘拟合的方法获得。再分析数据包含全球范围的近地面气温、露点温度、气压、大气可降水量以及晴空大气下行长波辐射值，时间分辨率为1 h，空间分辨率为0.25°。为了充分考虑不同气压条件下长波辐射的差异，本研究对拟合数据进行了筛选，将每小时全球各点的气压值均从小到大排序并形成十个区间，在每个气压区间中随机挑选100个气压值，对应100个地面点，拟合样本容量为288 000个。作为示例，图 1给出了经筛选后2018年1月1日00时全球范围内用于拟合的数据对应的地面点分布，红色的点表示此时经过筛选的站点。

从图 1中可以看出，青藏高原地区等高海拔地区数据覆盖程度较高，因此晴空数据筛选结果能够更好地保证高海拔地区拟合结果的准确性，这也正是对再分析数据进行筛选的目的。在此基础上经过最小二乘拟合处理后，得到三种考虑气压影响的晴空下行长波辐射参数化方案的经验系数见表 1。

为了研究上述三种参数化方案对晴空大气发射率的模拟效果，本文将对应时间ERA-5再分析数据中获得的所有站点的晴空大气发射率作为参照(即实际值)，分别求得三种参数化方案模拟结果的平均偏差、均方根误差及与参照大气发射率的相关系数并做散点密度图，同时将Prata模型的模拟结果作为对照，比较不同的参数化方案的模拟精度。

图 2a~2d分别给出了本研究提出的三种新参数化方案及Prata参数化方案在全球按海拔均匀分布的多个随机站点(包含平原地区和高原地区)的晴空大气发射率散点密度，模拟时间为2018年每月1日，时间分辨率为1 h，样本容量为288 000。图中横轴为根据ERA-5再分析数据中晴空下行长波辐射得到的晴空大气发射率，根据式(1)有：

$ \varepsilon = \frac{{L{W_{\rm{d}}}}}{{\sigma T_{\rm{a}}^4}} $

(10)

纵轴为考虑气压的参数化方案与Prata参数化方案，分别通过ERA-5气压与可降水量数据计算得到的晴空大气发射率理论值，颜色表示散点密度，颜色越亮则该区域散点密度越大。从图中可以看出，考虑气压影响的三种参数化方案得到的晴空大气发射率理论值与实际值基本上表现出斜率为1的线性关系，而对于Prata参数化方案而言，由于其在大气可降水量不断减小时大气发射率逐渐收敛于0.665左右，因此对于大气发射率小于该极限值的情况无法进行模拟，这也解释了该参数化方案应用于大气可降水量较小的地区时而造成精度较低的问题。三种考虑气压的参数化方案与Prata参数化方案晴空大气发射率模拟结果相较于ERA-5数据的平均偏差(MBE)、均方根误差(RMSE)及相关系数(R)计算结果见表 2。

从表 2中可以看到，相对于ERA-5再分析数据，方案2和方案3的MBE较小，其中方案3的MBE仅为4.36×10^-5，Prata参数化方案的MBE较大，为0.068；对于RMSE和R而言，方案1、方案2及方案3亦均显著优于Prata参数化方案，其中方案2和方案3精度更高，相关性更好。因此，本研究所提出的三种参数化方案相比Prata的参数化方案能更精确地对晴空大气发射率进行模拟，尤其是在高海拔大气可降水量较小的区域，理论上能够弥补Prata参数化方案过早收敛的缺陷。

3 适用性分析

上一节中晴空大气发射率参数化方案的拟合数据是经过筛选的全球数据，因此理论上三种新的参数化方案可对全球范围具有不同气压和可降水量条件地区的晴空下行长波辐射进行模拟。为了进一步分析三种新的参数化方案在青藏高原及其他地区的适用性，本研究对青藏高原及其他地区的晴空下行长波辐射进行了理论计算，以位于青藏高原的安多县(海拔5 200 m)和位于阿根廷圣路易斯(海拔500 m)的两个站点为例，本文给出了利用站点数据对新方案与Prata方案的模拟效果进行比较的结果。

对安多地区晴空下行长波辐射的模拟使用了该地区1998年5月11日至9月16日的站点数据，包括气压、近地面气温、相对湿度等观测值。本研究通过计算云量的方法获取晴空时间(Zhu et al, 2017)：

$ n = 1 - \frac{{{S_{{\rm{in }}}}}}{{{S_{{\rm{clear }}}}}} $

(11)

式中：n表示云量，S_in表示实测太阳下行短波辐射值，S_clear为晴空时太阳下行短波辐射值，二者单位均为W·m^-2，后者可以通过理论模型计算获得。由于夜间太阳下行短波辐射减弱为0 W·m^-2，因此上述方法无法获取夜晚晴空时间，本研究仅取太阳天顶角小于70°且n值小于0.05时作为晴空。用于计算的大气可降水量无法通过观测获得，目前常用的推算大气可降水量的方法包括探空资料计算、地面气象资料推算、地基GPS探测资料反演等。由于目前探空资料和GPS数据较为缺乏，本研究中采用站点资料，根据经验公式计算青藏高原地区大气可降水量(Yang et al, 2010)：

$ w = 0.00493\frac{{R{H_{\rm{a}}}}}{{{T_{\rm{a}}}}}{{\rm{e}}^{\left({26.23 - \frac{{5416}}{{{T_{\rm{a}}}}}} \right)}} $

(12)

式中: RH_a为站点的相对湿度; w为大气可降水量，单位为g·cm^-2；T_a为气温，单位为K。得到晴空时间与可降水量后即可计算各参数化方案的晴空大气下行长波辐射理论值，并与下行长波辐射观测数据进行对比分析其误差。

图 3a~3d分别给出了根据方案1、方案2、方案3及Prata方案使用安多站点数据对该地区的晴空大气下行长波辐射的模拟结果。从图中可以看出，Prata参数化方案在青藏高原地区下行长波辐射较小时模拟效果较差，理论值普遍偏大，这与前面提到的该方案在晴空发射率较小时精度降低相一致。引入气压的三种新方案模拟的结果与下行长波辐射观测值更加吻合。表 3给出了该站点上述四种方案的MBE、RMSE及R。

从表 3中可以看出，三种考虑气压的参数化方案模拟结果的MBE、RMSE相对Prata方案均较小，说明引入气压后的参数化方案有效地改善了Prata参数化方案在青藏高原地区的模拟精度，在青藏高原的适用性更强。

由于圣路易斯与安多地区气象条件差异较大，本研究在对圣路易斯地区应用经验公式(16)计算理论大气可降水量时将理论可降水量与ERA-5再分析数据可降水量进行了比较，发现理论值较再分析数据普遍偏小，其RMSE达到6.6 g·cm^-2，因此该经验公式无法准确估计圣路易斯地区大气可降水量情况。为了验证引入气压的参数化方案在该地区的适用性，大气可降水量采用2014年ERA-5再分析数据，晴空时间的获取方法与安多地区相同。

图 4a~4d分别给出了根据方案1、方案2、方案3及Prata方案使用站点数据对圣路易斯地区的晴空大气下行长波辐射的模拟结果。从图 4d中可以看出，Prata参数化方案的晴空下行长波辐射模拟结果相比于ERA-5再分析数据普遍偏大，而引入气压的新参数化方案理论值与再分析数据的吻合情况更好。表 4给出了圣路易斯地区上述四种方案的MBE、RMSE及R。

根据表 4可知，考虑气压的新方案的MBE、RMSE均明显小于Prata参数化方案，三种新方案的模拟精度相当，方案2的RMSE最小，为14.393 W·m^-2，方案1和方案3的RMSE相对较大，分别为16.043和15.937 W·m^-2，因此在圣路易斯地区方案2的模拟精度相对更高，而考虑气压的参数化方案相较于Prata方案适用性更强。需要指出的是，本研究中参数化方案的适用性分析没有考虑局地校正，而是将最小二乘拟合结果直接应用于不同气压条件的站点，分析引入气压后的方案相对于不考虑气压的方案的改善情况，而结合对安多地区和圣路易斯地区模拟结果的分析可知，新参数化方案对不同地区晴空大气下行长波辐射理论计算的精度均有较为明显的改善。

4 结论与讨论

本研究基于Prata提出的晴空大气下行长波辐射参数化方案，针对其对高原地区下行长波辐射模拟结果误差较大及可降水量较小时大气发射率过早收敛的问题，考虑到不同长度的大气柱下行长波辐射发射量不同，通过引入气压作为新变量提出了三种新的晴空下行长波辐射参数化方案。新方案保留了Prata参数化方案的优点，当大气可降水量趋近于0时，大气依然发出下行长波辐射，此时晴空大气发射率收敛为一个常数，且该参数化方案估算的晴空大气发射率不会超过黑体的发射率。新方案的经验参数由全球ERA-5再分析数据通过最小二乘拟合的方式获得，在拟合的过程中充分考虑了高原地区大气压偏小的特点。本研究在不同地区使用新的参数化方案对晴空大气下行长波辐射进行了模拟，通过模拟精度的比较分析其在不同气象条件下的适用性。青藏高原的安多地区下行长波辐射模拟结果表明，引入气压的三种新的参数化方案能有效地改善Prata参数化方案在水汽较少时模拟精度明显降低的缺点，相对于下行长波辐射观测结果，三种新方案模拟结果的MBE分别为-1.596、-0.205和1.810 W·m^-2，RMSE分别为13.731、13.930和14.374 W·m^-2，较Prata方案均更小，表明在青藏高原等高海拔地区新方案的适用性优于Prata方案。对南美洲圣路易斯地区的晴空下行长波辐射模拟结果表明，Prata参数化方案的模拟结果相对于ERA-5再分析长波辐射数据整体偏大，其MBE、RMSE分别为22.853和26.803 W·m^-2，而新方案的模拟结果与再分析数据更加吻合，MBE分别仅为3.327、4.443和7.956 W·m^-2，RMSE也有明显的改善，分别为16.043、14.393和15.937 W·m^-2，因此在低海拔地区，引入气压的新参数化方案的适用性同样优于Prata参数化方案。

为了便于研究引入气压后的参数化方案相比于Prata方案模拟精度上的提高，分析不同方案的适用性，本文中的Prata参数化方案与考虑气压的新方案在适用性分析的过程中均没有经过局地校正，而事实上，下行长波辐射参数化方案经过局地校正后能有效地提高模拟精度。局地校正指的是确定参数化方案后，以特定的站点或区域数据为依据对方案进行拟合确定经验常数的方法，通过局地校正通常可以获得适用于该地区或该站点且精度较高的理论模型，例如Zhu et al(2017)研究指出，经过局地校正的青藏高原慕士塔格峰、扎当冰川等地的下行长波辐射参数化模型相较于未进行局地校正的模型，其MBE由-6 W·m^-2减小为0.1 W·m^-2，RMSE由14 W·m^-2减小为9.6 W·m^-2(Zhu et al, 2017)，因此本研究的三种考虑气压的参数化方案有望在局地校正后获得更高的精度，这会在将来的研究中加以验证。此外，由于大气可降水量无法直接观测，利用站点数据对下行长波辐射进行理论精确模拟需要具备适用于该站点的大气可降水量模型，根据本文对可降水量理论计算的结果可知，现有的可降水量模型无法适用于不同气象条件的站点，因此发展能精确计算站点大气可降水量的理论模型，也需要在将来的研究中进一步考虑。