引言

近几年我国气象部门大力开展智能网格预报业务，要求24 h预报时间分辨率达到1 h。在智能网格预报中，高分辨率模式的主导地位更加突显，模式性能的提升无疑决定了未来预报业务的主要发展方向。目前高分辨率模式仍存在诸多局限，主要来自于初始条件、边界条件、物理过程、同化技术、模式适用性(漆梁波，2015)等方面，因此模式订正技术的发展亦不可忽视。合理、客观、定量的订正方法是连接数值模式与精准预报的桥梁，是深入挖掘数值预报潜力不可或缺的环节，也是未来一段时间高分辨率模式应用的关键。

目前，基于经典统计学方法的温度预报订正技术已经优于预报员预报水平(吴启树等，2016)，在较长时间的累积降水量预报方面也有所进展，诸如频率匹配法(李俊等，2014；2015)、评分最优化订正法(吴启树等，2017)等方法被广泛使用。但是对于精细到逐小时的降水预报订正方法研究仍然比较匮乏。归根结底在于气温与降水两种要素存在巨大差异，与气温演变所表现出的连续性和平稳性不同，降水事件在时空分布上具有高度的非线性和随机性，从逐小时的降水事件来看这种随机性更加显著，所以传统的统计学方法对其订正作用十分有限。近年来，人工智能逐渐在图像识别、数据挖掘及医疗等诸多领域中得到了良好的结合与深入的应用，甚至为部分行业带来前所未有的变革，这对于现阶段预报技术发展具有重要的启发意义。气象数据是名副其实的“大数据”，而人工智能的前沿技术——深度学习(deep learning，DL)是迄今为止处理大数据的最有效算法之一。相比其他机器学习算法，DL的优势在于学习能力进一步增强，对各类复杂问题的适应性好，其数据驱动的特性尤其适用于对大数据包含的丰富信息进行自动挖掘。如何将DL应用于数值预报订正将是我们必须思考的问题。

近年来，DL在气象领域的结合应用案例日益增多，并展现出了巨大的潜在价值与广阔的应用前景(许小峰，2018)。孙全德等(2019)将DL应用于数值模式10 m风速预报的订正上，发现随着预报时效的增加，订正力度越来越大；Shi et al(2015；2017)将卷积长短期记忆(convolutional long-short term memory，LSTM)网络模型应用于临近降水预报，相比于光流法展现出了更优秀的预报能力，在此基础上又进行了网络结构的改进，在预测效果基本不变的前提下减少了冗余参数；针对雷达资料这种典型的时空结构数据，郭瀚阳等(2019)发现DL可以有效“学习”到雷达数据特征的内在关联，明显提高了强对流回波临近预报准确率；滕志伟(2017)根据LSTM对雷达回波外推问题的实践，提出了一种基于LSTM的RET-RNN模型，并对RET-RNN模型的结构和超参数进行了优化，该算法在外推时效较长时效果较好。卷积神经网络(convolutional neural network，CNN)是DL中一种经典的网络结构，其具有的局部连接、权值共享及池化操作等特性有效减少了冗余参数，易于训练，鲁棒性较强(周飞燕等，2017)。也由于这些优越特性，基于经典卷积神经网络LeNet-5的各类“升级版”网络模型在多届ImageNet大规模视觉识别挑战竞赛(imagenet large scale visual recognition challenge)中蝉联冠军，甚至超越了人类自身的识别水平。

然而，目前DL在气象领域的应用思路仍然集中在如何根据实况观测资料推测预报对象未来的演变过程，DL与数值预报的融合应用之先例相比甚少。能否在快速更新同化预报系统对未来几个小时的环流形势和环境条件预测的基础上进一步通过DL“推导”出相应的降水状况，是具有研究价值和实践意义的问题，亦是本文的研究重点。天气演变过程本质上仍是物理演变过程，任何尺度上的物理机制都必须受到物理定律的约束，这方面正是DL所不擅长的。DL仍是一种统计意义上的技术，只不过它的高度非线性变换能力赋予了它一定程度的“智能”，但在现阶段仍难以胜任模拟物理动力过程的任务。合理运用DL作为数值预报的“辅助”手段对其进行后处理，意味着把DL不擅长的物理过程演变问题转化为DL比较擅长的模式偏差订正问题，是两者取长补短的极佳结合点。本文应用历史观测资料与数值预报产品，建立和训练了基于卷积神经网络的逐时降水分级订正模型，并与频率匹配法进行2017—2018年测试集的对比试验和2019年数据集的模拟业务检验以评估模型订正效果，同时探讨了试验过程中遇到的样本不均衡、特征变量选取以及模型过拟合问题，为DL在气象领域的应用和数值预报后处理技术的发展提供了新的思路。

1 资料 1.1 观测资料

本试验主要针对福建省强降水频发的主汛期，选取2017—2019年5—9月福建省内自动站逐时雨量数据作为观测资料。具体空间范围为23.32°~28.51°N、115.68°~120.69°E，除省界边缘的少数站点外，涵盖了福建省内约2 200个雨量站。其中，从逐时、逐站的角度对2017—2018年观测资料进行采样以制作K折交叉验证的试验数据集，可得到约1 400万站次的有效样本；同样对2019年观测资料进行采样以制作用于模拟业务检验的数据集，约有736万站次的有效样本。根据业务实践将逐时雨量分为四个等级，通过观察样本分布情况(表 1)可以发现，逐时雨量数据存在着严重的不均衡特征，中等以上降水属于极小概率事件，所占比例大约只有0.3%，这也是在后续模型训练过程中必须处理的问题。

1.2 预报资料

采用华南区域中尺度模式系统(GRAPES Tropical Regional Modeling System，GTRAMS)提供的预报产品。该模式系统采用具有区域特点的三维参考大气动力框架及高分辨率地形数据集，辅以快速更新的雷达资料云分析技术，形成了一套区域内的逐小时快速更新同化预报系统GTRAMS-3 km-RUC(徐道生等，2014)，以下简称RUC。

选用2017—2019年5—9月的RUC历史预报产品作为预报资料。RUC产品的水平空间分辨率为0.03°×0.03°，垂直方向上分为12层，预报间隔为1 h。RUC预报产品种类丰富，其中包括涡度、散度、假相当位温、水汽通量散度等19种物理量产品。值得一提的是，RUC在2019年5月进行了一次较大调整，预报性能有所提升，但预报误差的分布也相应发生改变，因此应用2019年RUC预报资料进行模拟业务检验更能考验各订正方案的稳定性和适应性。

2 模式降水预报检验 2.1 检验方法

空间上，将RUC逐时降水预报的格点场通过最邻近法插值至观测站点；考虑到实际业务中存在的计算延迟，预报时效为3 h的模式资料具有较大的实际应用价值，故重点选取预报时效为3 h的模式预报进行分级检验。检验指标包括TS评分(TS)、ETS评分(ETS)、漏报率(PO)、空报率(FAR)、偏差(Bias)，各指标公式如下：

$ T S=\frac{N A}{N A+N B+N C} $

(1)

$ \begin{array}{l} E T S=\frac{N A-r}{N A+N B+N C-r} \\ r=\frac{(N A+N B)(N A+N C)}{N A+N B+N C+N D} \end{array} $

(2)

$ P O=\frac{N B}{N A+N B} $

(3)

$ F A R=\frac{N C}{N A+N C} $

(4)

$ Bias=\frac{N A+N C}{N A+N B} $

(5)

式中：NA为对应降水等级预报正确的站数，NB为漏报站数，NC为空报站数，ND为其余降水等级预报正确的站数。

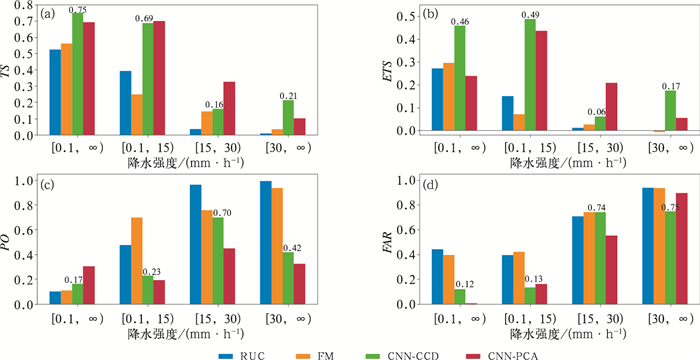
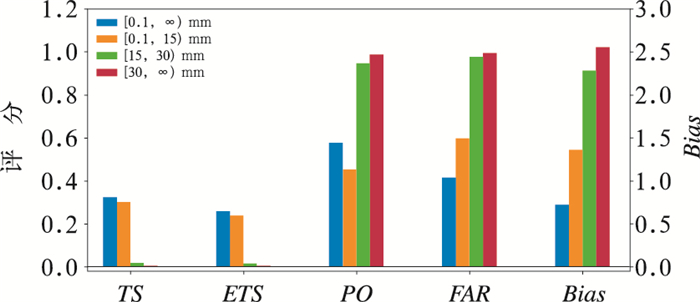
2.2 检验结果

由图 1可见，在2017—2018年5—9月RUC对于站点的逐时降水预报能力随着降水量增大而急剧减弱。晴雨和弱降水预报的TS评分与ETS评分相对较高，而超过15 mm·h^-1时均降至0.02以下；对于15 mm·h^-1以上降水预报的漏报率和空报率均超过0.9。从偏差来看，晴雨预报存在干偏差，而各降水等级的预报却存在明显的湿偏差，尤其是15 mm·h^-1以上降水的偏差达到2.2以上。从站点检验的角度来看，RUC对于中等以上降水预报基本失去参考意义。

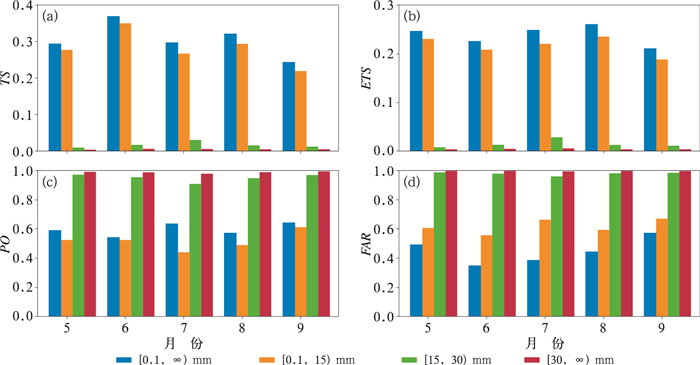
从图 2观察评估指标的月变化规律，发现RUC在各月的预报能力变化幅度较大。晴雨和弱降水的TS评分在6月达到最高，9月为最低；而从ETS评分来看，却是在8月表现最优，其余月份的差异相对较小；中等以上降水的TS评分和ETS评分均是在7月相对高一些。从图 2c和2d对比发现，晴雨预报的漏报率在所有月均高于空报率，而弱降水则相反；整体来看，9月的漏报和空报情况最为严重。造成这种月变化规律的主要原因可能是RUC对不同性质降水过程的预报能力存在明显的差异。

另外也以相同方法分别检验了预报时效为6、9和12 h的RUC降水预报(图略)，发现在TS、ETS、PO、FAR四项指标上的各分类预报相对水平分布均与预报时效3 h一致，差别在于随着预报时效的延长，这四项指标的绝对水平均呈现不同程度的转差趋势，如预报时效12 h的晴雨预报TS和ETS分别下降至0.15和0.08。在15 mm·h^-1以上降水预报的Bias则发生了较大变化，原先的显著湿偏差随着预报时效延长而迅速减小，预报时效12 h的中等降水和强降水预报Bias已分别降至1.31和1.10，甚至略低于同时效的弱降水预报Bias。

总之，尽管RUC预报具有较高的时空分辨率，但降水预报效果仍然不够理想，尤其是针对15 mm·h^-1以上量级的降水预报能力较差，需要合理的客观解释应用方法加以订正。

3 基于卷积神经网络的降水预报订正方案 3.1 基本原理

卷积神经网络的基本结构一般由输入层、卷积层、池化层、全连接层及输出层构成。在卷积层中，卷积核是一个权值矩阵(如对于二维平面而言可为3×3的矩阵)，它以固定顺序逐步滑动作用于原始输入矩阵，然后生成一个新矩阵，即新矩阵的元素为：

$ s(i, j)=\sum\limits_{m} \sum\limits_{n} x(i+m, j+n) w(m, n) $

(6)

式中：x为原始矩阵中的元素，s为新矩阵的元素，w为卷积核的权重，m、n分别为卷积核的列数、行数。卷积层通过卷积操作和激活处理(如ELU、RELU函数)提取特征，底层的卷积层用于提取低级特征，更高层的卷积层通过组合低级特征而提取出更高级的特征。为了让模型具备一定的泛化能力，紧跟在卷积层之后加入池化层，通过取最大值或平均值的方式来进一步降低分辨率，这种操作可以使卷积神经网络的识别获得平移不变性。通过多次卷积层和池化层的计算之后，中间变量进入全连接层，全连接层可以整合具有类别区分性的高维信息，然后输出最终的结果。

模式预报的物理量格点场与普通的图像数据具有许多相似之处：物理量的水平空间分布如同图像的像素矩阵，物理量的种类与层次则可类比于图像数据中的“通道”概念。订正模型试图借助卷积神经网络在识别领域的巨大优势以挖掘物理量场与逐时雨量等级之间可能存在的映射关系。然而，若将预报范围内的全部网格数据直接用于模型输入，则对于同一时刻的不同站点而言，其输入变量均不变，难以得到有意义的输出结果。为此需要构建属于单个站点“特有”的输入变量，采样方案为：以站点为中心，截取固定范围的矩形区域内的格点数据作为输入变量，即认为“局部”的物理量场与该站点的逐时雨量之间存在对应关系。这种从站点角度进行建模的优势在于不仅使自变量与因变量的对应关系变得更加清晰明朗，而且能够利用的数据量大幅增加，十分利于提升模型的学习效果。

3.2 方案设计 3.2.1 数据预处理

根据时空对应关系将观测资料与模式预报资料制作成数据集。空间上，以预测站点为中心截取出边长约为45 km的矩形网格作为输入变量；时间上，选取预报时效为3 h的预报产品作为对应的预报资料。

一般而言，图像矩阵在输入模型之前需要进行标准化或归一化处理，物理量数据包含各种不同量纲的物理量，所以同样需要类似的预处理。但物理数据不同于图像像素值存在着明确的上下限，而且不仅物理数据的空间分布是关键信息，其数值的相对高低对模型输出亦有至关重要的影响。为了较好地保留物理量场的空间分布以及数值区间的信息，采用先标准化后缩放计算的预处理方案：先计算出每种物理量场的空间平均值M，再对均值序列进行标准化处理，将标准化值与原先的空间平均值M之比作为缩放系数，最后将每个原始样本与对应的缩放系数相乘即得到比较合适的新样本数据。即对于每个样本中的物理量矩阵X作如下变换：

$ \boldsymbol{X}^{\prime}=\boldsymbol{X} \cdot \frac{\operatorname{std}(M)}{M} $

(7)

3.2.2 特征变量选取

模式生成的预报产品种类丰富，部分还涉及不同的高度层次，如果不加以筛选而将所有物理量作为输入特征变量，则由于物理量之间并非相互独立以及对模型输出的敏感性差，很可能导致订正效果大打折扣。这里采用两种特征变量选取方案进行对比试验，分别是相关系数判别(correlation coefficient discrimination，CCD)和主成分分析(principal component analysis, PCA)。前者根据物理量与小时雨量的相关系数绝对值大小进行挑选，以0.15为阈值从45个不同种类、不同层次的物理量中挑选出22个作为特征变量，该阈值已通过α=0.01的显著性水平检验，结果如表 2所示。后一种方案则是在预处理后对所有物理量进行主成分分析，由于输入特征变量的数目对模型训练存在影响，为了便于和前一种方案对比，也从45个主成分中挑选前22个主分量作为特征变量，这22个主分量的总解释方差比例已经超过了97%，可见PCA的特征降维作用十分明显，具体方案为：先对训练集中每个样本的场均值进行标准化处理，然后对标准化的场均值所组成的新序列进行主成分分析，获取的主分量变换系数将应用于对应样本的逐个格点上(经过如3.2.1节的预处理之后)，从而构造出浓缩了绝大部分旧变量变化信息的新变量。

3.2.3 K折交叉验证下的数据集划分

深度学习建模的核心在于训练过程，训练数据分布状况的好坏将会直接影响模型最终的学习效果。为了削弱这种数据随机性所导致的模型不稳定性，应用K折交叉验证方案将2017—2018年5—9月样本数据划分为8份，每份数据中的各等级降水样本比例均与总体保持相同。每次建模使用其中的7份作为训练集，剩余1份作为测试集，最后将8次试验的平均结果作为评估指标。为了避免数据不均衡问题导致模型训练出现“一边倒”的情况，采用随机欠采样方案使训练集样本分布保持平衡，即以强降水类的样本数为参考标准，从其他类中随机抽取相近数目的样本加入，缺点是其他类的数据利用率降低。另外，为了最大限度地利用现有数据集，从测试集中随机抽取80%的样本作为验证集，该做法不会影响试验的客观性，验证集的加入可以方便地跟踪模型在每一代训练阶段后其拟合能力和泛化能力的变化趋势。最终每次试验所用的数据集数量分布如表 3所示。

另外，应用2019年5—9月观测数据与相应的RUC预报资料制作用于模拟业务检验的数据集。2019年数据集包含了19 566个中等降水样本和5 323个强降水样本，另外分别随机抽取了50 000个无降水和50 000个弱降水的样本加入，样本总数共计为124 889个。该数据集体现了气象数据所具有的时间关联特征，能够为基于前两年数据训练而得到的订正模型提供比较真实的模拟测试条件。

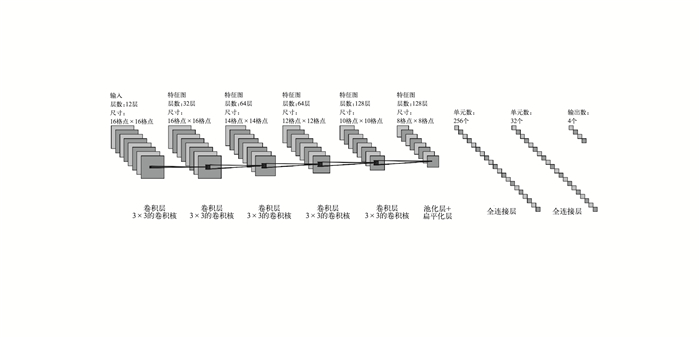
3.2.4 模型设计

试验设计的订正模型符合经典卷积神经网络的拓扑结构(图 3)，可训练的总参数量在81万个左右。第一层卷积层的卷积核尺寸设为1×1，主要目的在于使相对“平滑”的物理量场的空间分布信息更加突显，其余卷积层均采用3×3的卷积核。同时，考虑到截取的“局部”物理量场空间范围并不是太大，所以只在最终的卷积层之后才加入池化层，避免过度压缩导致丢失大部分信息。为了进一步加快收敛速度和减轻过拟合的影响，模型中加入批规范化层(Ioffe and Szegedy, 2015)和随机失活层(Liang and Liu, 2015)。最后由Softmax函数(Wang et al，2018)进行各个雨量等级的概率分布回归，挑选出最大概率的降水等级作为模型输出结果。模型训练的损失函数设为多分类交叉熵(cross-entropy，CE)(Kline and Berardi, 2005)，其公式为：

$ C E=-\sum\limits_{i=1}^{n} o_{i} \cdot \log \left(f_{i}\right) $

(8)

式中：o_i为观测值，f_i为预报值。交叉熵是度量两个概率分布间的差异性信息的指标，其保持高梯度状态的特性可以使模型的收敛速度基本不会受到影响。

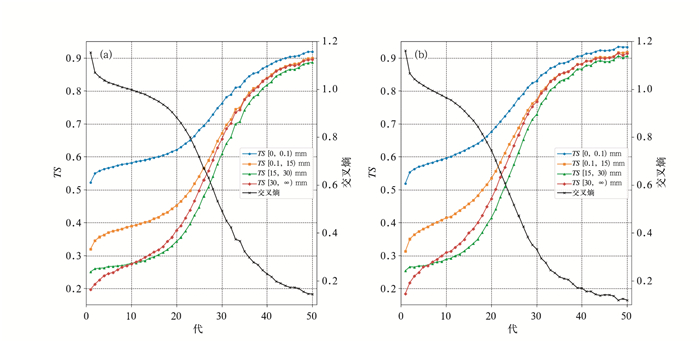
4 试验对比 4.1 不同特征变量选取方案下的训练过程对比

分别应用CCD和PCA两种特征变量选取方案对基于卷积神经网络的相同模型进行50次迭代训练，以8次交叉验证试验的平均TS评分作为跟踪指标观察模型在训练过程中的性能变化趋势。如图 4所示，两者在训练集上的TS评分和交叉熵变化均表现出“S”型曲线特征，总体趋势无显著差异。开始训练时模型的识别能力类似于模式的原始预报，与降水强度成反比，第25代训练以后，模型在训练集上的TS评分均超过了0.4，交叉熵降至0.6以下，反映了模型的拟合能力随着训练过程而显著改善。随着迭代数继续增加，模型不断加速收敛，对训练集中各个等级降水识别能力的差异性逐渐减小。最终TS评分达到0.8以上时收敛速度放缓，达到了理想的水平。在训练集上两个方案的最大差异在于PCA方案的训练指标改善速度更快，后期能够达到的极限水平也略高一些，这意味着PCA方案确实起到了压缩特征变量信息的作用，挑选出来的主分量可使模型的拟合能力进一步增强。

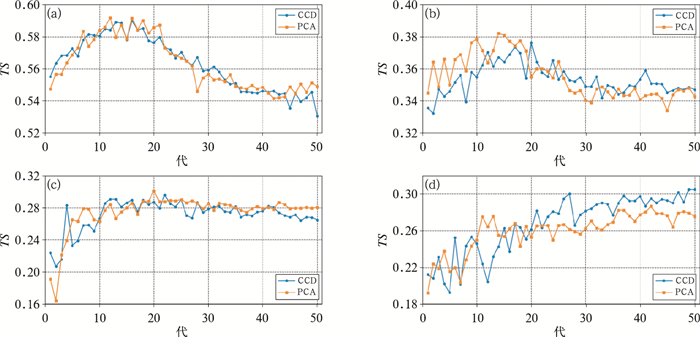
另一方面，模型在验证集上表现出较大反差(图 5)。模型对于陌生数据的识别能力在前15代中快速提升，之后根据降水等级表现出不同的变化趋势。无降水和弱降水的过拟合问题相对于中等降水和强降水更加严重，其评估指标在20代之后随着模型泛化能力转差呈现下滑的趋势。模型对中等降水的识别能力也在20代之后逼近极限，处于小幅振荡状态，对强降水的识别能力则一直缓慢提升。综合来看，本试验中订正模型对应的最佳训练期应在20代之前，20代之后的训练过程对于模型泛化能力的改善可能产生负作用。作为对比，同样计算得出RUC原始预报在8次验证试验中的平均TS评分，无降水、弱降水、中等降水、强降水分别为0.428、0.260、0.050、0.013，可见虽然模型出现过拟合现象，但是对RUC原始预报仍存在显著的改善作用，尤其对于中等降水和强降水的预报。另外，模型对中等降水和强降水的“学习”效果均优于另外两个等级，两者第20代的TS评分相比第1代分别提升了35%和36%左右。

进一步对比两种特征变量提取方案带来的差异。PCA方案在训练集上的收敛速度更快，从第10代起各项指标已明显超越了CCD方案，但也更早进入过拟合状态，40代之后模型严重的过拟合状态导致各项指标已难以继续提升。验证集上看，前期PCA方案下的TS评分在弱降水和强降水情况下优于CCD方案，但随着训练代数增加反而变得与CCD方案持平或者更差，其原因可能是PCA方案下的模型更早(20代前后)进入严重的过拟合状态，这也意味着更早进入“负效果”的训练阶段；相反地，CCD方案的模型学习能力却还在不断增强，后续达到了更具“潜力”的状态。不可忽视的是，验证集样本数量小于测试集和训练集，产生的随机性也会相对更大一些。

4.2 不同订正方案在2017—2018年测试集上的对比

为了评估模型的订正效果，在2017—2018年测试集上对比RUC原始预报以及频率匹配法(frequency matching，FM)、CCD方案下的模型(以下简称CNN-CCD)和PCA方案下的模型(以下简称CNN-PCA)这三种不同的订正方案。其中，FM的滑动统计窗口设为10 d。另外，根据CNN-CCD和CNN-PCA在验证集上的表现，分别选取第20代和第14代模型作为最佳训练期进行对比检验。

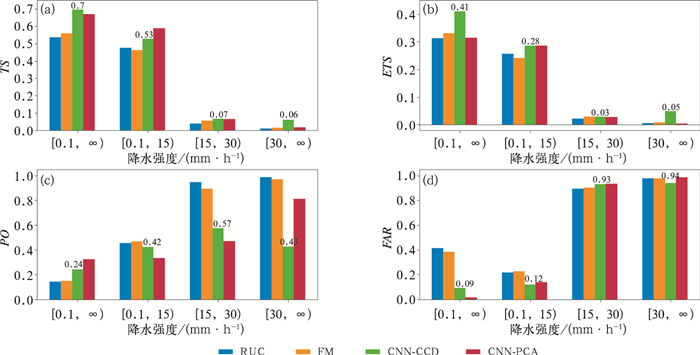
通过图 6a和6b可以看到，虽然基于卷积神经网络的订正模型出现过拟合问题，但仍然对RUC原始预报带来了一定程度的提升，尤其在晴雨、弱降水和强降水预报下订正效果更加显著，CNN-CCD在这三种情况下的TS评分分别为0.697、0.528和0.060，其相对于原始预报的技巧评分分别达到了0.160、0.052和0.051，比FM分别高出了0.137、0.066和0.046，其针对30 mm·h^-1以上的降水提升幅度最大。CNN-CCD与CNN-PCA的差异主要体现在强降水样本上，CNN-PCA对强降水等级的预报无明显改善作用。FM对RUC原始预报亦有微弱的改善作用，但是总体不如CNN-CCD与CNN-PCA。另外，无论哪种方案对中等降水等级的订正效果均为最差，甚至不如RUC原始预报，原因可能有二：RUC本身对于中等降水事件的预报能力已经足够优秀，可订正空间有限；中等降水对应的物理特征不够突出，难以和弱降水或强降水相互区分，导致“学习”难度大。

从漏报率和空报率分析不同方案的误差订正来源：CNN-CCD和CNN-PCA均能大幅减少中等降水预报的漏报率，但晴雨预报的漏报率却不降反升。另外，CNN-CCD大幅削减了强降水的漏报率，其削减率可达原始预报的56.8%，而CNN-PCA则在弱降水漏报率上表现最优。由图 6d可见，CNN-CCD和CNN-PCA均无法改善中等以上降水的空报率，但能够显著改善晴雨和弱降水的空报率。相比而言，频率匹配法对漏报率和空报率的削减幅度亦不如另外两种方案。总体来讲，CNN-CCD和CNN-PCA可以取得更加理想的订正效果，特别是CNN-CCD对强降水等级预报的订正十分有效。

4.3 不同订正方案在2019年数据集上的对比

为了更加真实地对比不同订正方案在实际业务应用中的表现差异，制作了2019年数据集进行检验。RUC在2019年5月进行了性能升级，进一步加大了不同方案的适应难度，能够更好地模拟完全陌生的实际业务数据环境。

首先从图 7观察到不同订正方案在2019年数据集上的表现差异不同于2017—2018年的测试集，主要原因是模式调整带来的误差分布变化，但仍然可以发现CNN-CCD和CNN-PCA在TS评分和ETS评分上基本超过了FM。从TS评分上看，CNN-CCD和CNN-PCA在晴雨预报和弱降水预报上差异不大，均超过了0.68的水平，而在中等降水和强降水上表现却截然相反，中等降水来讲CNN-PCA更优，这也是两个测试集之间具有较大差异之处；而在强降水上则是CNN-CCD显著超过CNN-PCA和FM，甚至达到了0.2以上。ETS评分的趋势与TS评分基本一致。

另外，图 7c的漏报率对比体现了CNN-PCA在分类订正方面更胜一筹，尤其是在弱降水和强降水预报上对漏报率的改善效果十分突出，但晴雨预报的漏报率反而最高。空报率方面，CNN-CCD和CNN-PCA的订正作用均主要体现在晴雨预报和弱降水预报上，中等降水和强降水的空报率削减幅度较不明显。通过在2019年测试集上的进一步检验可以看到，CNN-CCD和CNN-PCA对未知数据的稳定性和适应性均优于传统的统计方法，具备较高的实际业务应用价值。

5 结论与讨论

本文从站点的角度检验了RUC在福建省5—9月的逐时降水预报性能，建立和训练了基于卷积神经网络的逐时降水分级订正模型，应用CCD和PCA两种不同方案提取模式预报物理量作为输入特征变量分别在2017—2018年的K折交叉验证测试集和2019年的模拟业务数据集上进行订正试验，并与频率匹配法对比分析订正效果。试验结果表明：

(1) RUC的晴雨预报存在干偏差，其分类降水预报却存在湿偏差，对于15 mm·h^-1以上降水的预报能力弱。从TS评分上看，各订正方案对RUC原始预报均有不同程度的改进作用，但频率匹配法对弱降水预报反而起到负的订正作用。传统的频率匹配法直接从频率统计的角度改善模式降水预报的系统性误差，CNN-CCD与CNN-PCA则能够通过模式对环境条件的预报信息推测出降水分类结论，两者原理截然不同。从各类评估指标来看CNN-CCD与CNN-PCA对原始预报的提升幅度更加突出，尤其对晴雨和弱降水的改善效果更加理想，其中CNN-CCD对30 mm·h^-1降水预报的订正十分有效。

(2) 在模型的输入特征变量选取方面，PCA方案下训练时的收敛速度较快，最佳训练期有所提前，但也更早进入严重的过拟合状态，这也意味着更早进入“负效果”的训练阶段。相反，CNN-CCD在训练过程中表现出了较长的提升期，从而在强降水预报方面达到了更具“潜力”的状态。

(3) 基于卷积神经网络的订正方案对减少分类降水预报的漏报率、晴雨和弱降水预报的空报率具有显著作用，优化程度明显超过频率匹配法。

(4) 试验所设计的CNN-CCD对应的最佳训练期在20代左右，CNN-PCA对应的最佳训练期在14代左右。模型表现出来的过拟合问题反映了其拟合能力较强、泛化能力较差的缺陷，最主要原因可能是各类样本可分性较差、训练样本数量与模型容量不相适应等，下一步将针对此问题继续优化和改进。