引言

以地区电力负荷特性分析为基础，开展地区电网短期负荷预测研究，是提高地区电网短期负荷预测精度的有效途径，有利于提升当地发电设备利用率和经济调度有效性(康重庆等，2007)。短期电力负荷预测是指预测未来几小时、一日或者几日的电力负荷，是电力负荷预测的重要组成部分。短期电力负荷预测的结果可指导调度部门安排机组日发电计划和跨区域的平衡调度(康重庆等，2004)；对电力系统的安全、可靠运行，提高电网的供电质量有着重要的现实意义。随着国民经济的发展和人们生活水平的提升，带来更多的制冷和取暖设备的使用，使得电力负荷尤其是居民用电负荷受气象因素间的影响增大(胡江林等，2002b )。因此，电力负荷与气象因素间的定量分析已成为众多学者的研究重点。

许多研究表明(Le Comte and Warren, 1981; Quayle and Diaz, 1980; 郑贤等，2008；杨静等，2010；李湘华等，2012；高亚静等，2017)，气象因素是造成电力短期负荷变化的重要原因之一，可引起30%左右的电力负荷上升(廖峰等，2012)。由于气候条件、经济结构和发展水平的不同，各电网电力负荷与气象因子的关系也不尽相同(叶殿秀等，2013)。北京逐日最大电力负荷具有明显的线性增长趋势；夏季日最大负荷星期效应显著；温度、风速和相对湿度与日最大电力负荷的相关显著(张自银等，2011)。日平均气温大于20℃时，华中电网日负荷与日平均气温为正的相关关系，小于20℃时为负的相关关系(胡江林等，2002a )。气温变化对南京城市日最大电力负荷和用电量具有不同的季节性和周期性影响(张海东等，2009)。尹炤寅等(2017)利用体感温度对电力负荷进行了精细的分解，体感温度同气象负荷率具有较高的关联度。傅新姝和谈建国(2015)基于滤波技术将日最大电力负荷进行了有效分离，建立的气象预报模型取得了较好的结果。

目前，在建立电力负荷预测模型时，多利用电力负荷或分离后的气象负荷与气温或多个气象因子之间的关系建立预报模型(叶殿秀等，2013；赵娜等，2017)；而对气象因子在电力负荷预测模型中的影响定量评估分析不足。同时，在所建立的预报模型中，前一日电力负荷对当日负荷影响的关注相对较少，而前一日电力负荷对提高模型预测精度却尤为重要(胡江林等，2002b)。

近年来，随着新能源利用的快速崛起，导致电网结构发生转变，且考虑全球气候变暖带来的可能影响，不同区域电力需求的变化及其影响因子可能更加复杂。夏季出现连续高温天气，往往会使电力负荷达到最高值或突破历史极值，使电网安全受到严重影响。2017年7月下旬，武汉遭遇连续高温的侵袭，使电网最大用电负荷急剧攀升，23日最大负荷超过10000 MW，28日达到最大值11018 MW。2018年夏季，受持续高温的影响，7月16—27日武汉日最大负荷连续超过10000 MW，并于26日达到最大值11353 MW，突破历史极值。因此，开展电力负荷特征分析及与气象因子的定量关系分析显得尤为重要。基于以上认识，本文利用逐步回归和BP神经网络算法，对武汉夏季日最大电力负荷进行了预测研究，定量评估了气象因子在电力负荷预测模型中的影响，以期为其他地区开展电力负荷和气象因子的影响研究提供参考。

1 资料与方法 1.1 资料来源

本文所用的电力数据为武汉市电力公司调度中心提供的2016年1月1日至2018年12月31日逐15 min电力负荷数据，每日共有96个电力负荷值，选取其中最大值作为日最大电力负荷。在此基础上，采用比较滤波法(王雁平和乐春峡，2007)对逐日最大负荷数据进行质量控制。

气象数据为湖北省气象信息与技术保障中心提供的经过质量控制后2016年1月1日至2018年12月31日逐日气象资料，包括平均气温、最高气温、最低气温、降水量、平均相对湿度、平均风速和日照时数。夏季时段选择6月1日至9月31日；本文所使用的人体舒适度指数参考《人居环境气候舒适度评价》国家标准(冯明等，2012)。

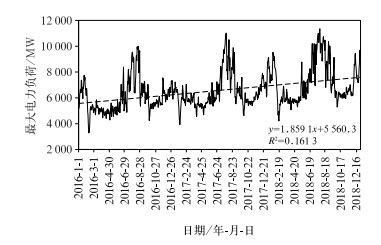
1.2 气象负荷的分离

图 1给出了2016—2018年武汉逐日最大电力负荷。可以看出，武汉地区年最大电力负荷总体呈现增长的趋势，增长系数通过0.05的显著性水平检验。年最大负荷呈现双峰型，第一次峰值出现在夏季，次峰值出现在冬季，且冬季最大电力负荷远小于夏季。日最大电力负荷波动变化特征显著，最大值与最小值相差在6500 MW以上。可见，武汉日最大电力负荷主要表现为随时间变化的趋势项，以及随不同时间尺度的气象因素、节假日和随机因素变化引起的波动项(陈正洪和洪斌，2000)。由于随机因素属于不可预测因素，对最大电力负荷的影响较小，本文重点研究受气象因素影响的波动项，称其为气象负荷。

根据陈正洪和洪斌(2000)的研究，利用最小二乘法将2016 —2018年逐日最大电力负荷分离出来，总负荷与负荷变化趋势的差值即为气象负荷。依据相关分析方法来分析气象负荷与气象因子的关系，利用逐步回归和BP神经网络方法建立武汉夏季日最大电力负荷的预报模型，并开展气象因子在最大电力负荷预测中的影响分析。

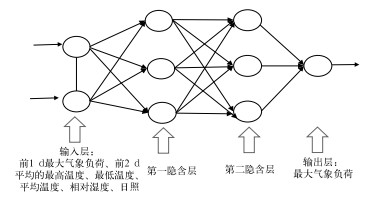
1.3 研究方法

BP神经网络核心是对实际值与预测值之间误差的一个反向传递过程，通过求误差对权值(或阈值)的导数，使权值(或阈值)不断地调整修正，最终将输出误差控制在允许范围内(Kacprzyk and Pedrycz, 2015)。通常包含输入层、隐含层和输出层，上下层实现全连接，而每层之间无连接。本文构建了多输入、单输出的双隐含层BP神经网络模型。输入层由n个节点组成，用于系统n个信号的输入；第一隐含层有m个神经元节点，用于完成输入信号的空间加权及激励输出；第二隐含层由k个神经元节点构成，用于提高网络对系统输入输出之间复杂关系的非线性映射能力；输出层由一个神经元节点构成，用于完成系统的输出(丁红等，2014)。本文所构建的多输入、单输出的双隐含层BP神经网络模型如图 2所示。

为表征气象因子在电网短期负荷预测中的影响，本文定义电力负荷气象敏感度(meteorological sensitivity，MS)，如果敏感度为正(负)值，表明气象因子对提高电力负荷预测精度为正(负)的贡献，计算方法如下：

$ M{S_{{\rm{SR}}}} = \frac{{|F{A_{SR - M}} - F{A_{{\rm{SR}}}}|}}{{F{A_{{\rm{SR}}}}}} \times 100\% $

式中：FA_SR表示直接依据电力负荷数据利用逐步回归方法得出的预测准确率，FA_SR-M表示依据电力负荷数据和气象数据利用逐步回归方法得出的预测准确率，MS_SR为逐步回归方法中气象敏感度。BP神经网络方法中气象敏感度计算方法与MS_SR类似，标记为MS_BP。

为了比较不同因子对负荷预测的影响，使用了三类模型。模型1采用前1 d最大气象负荷、前2 d平均的最高温度、最低温度、平均温度、相对湿度、日照时数共六个因子作为预报因子，模型2采用前1 d最大气象负荷作为预报因子，模型3采用前1 d舒适度作为预报因子。

2 负荷与气象因子的相关分析 2.1 与气象因子的关系

通过分析表明，去除了长期变化趋势后，气象负荷与平均气温、最高气温、最低气温及舒适度指数的相关性明显增强，相关系数提高了20%~40%，且均通过了0.01的显著性水平检验，表明气象负荷与气象因子的相关性更好(胡江林等，2002a )。因此，在进行夏季日最大电力负荷预测因子及模型的研究时，可用分离后的气象负荷代替原始最大电力负荷。

气象负荷与温度呈显著的正相关关系(表 1)，与平均温度、最高温度、最低温度的相关系数分别为0.78、0.76、0.64，且均通过了0.01的显著性水平检验，可见温度对夏季气象负荷变化的影响最为显著。此外，除温度要素外，日照时数与气象负荷也存在正相关关系，相关系数为0.47(通过0.10显著性水平检验)。由于日照时数的长短与气温变化存在较好的相关性，日照时数对夏季气象负荷也存在较大影响，在预测模型设置预报因子时也需考虑将其纳入。

相对湿度与气象负荷存在负相关关系，相关系数为－0.29，通过了0.10的显著性水平检验。综合考虑了温度和湿度的舒适度指数与气象负荷存在显著的正相关，相关系数高达0.74，表明夏季电力负荷的波动对舒适度的变化也很敏感。尽管不同月份的气象因子与气象负荷的相关系数存在一定差异，但气象负荷与平均气温、最高气温、最低气温、日照时数、人体舒适度存在稳定的正相关性，与相对湿度基本存在负相关，降水量、风速与气象负荷在不同月份的相关性差异较大，存在较大的不确定性。

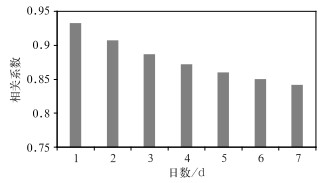
2.2 累积效应及周末效应的影响

由于历史气象负荷会对当日气象负荷产生重要影响，因此，本文首先分析了累积气象负荷因子与夏季最大气象负荷的相关性。将累积最大气象负荷定义为前1~7 d最大气象负荷的滑动平均，分别计算与当日最大气象负荷的相关系数，结果如图 3所示。可以看出，当日最大气象负荷与前1 d最大气象负荷的相关性最大，为0.93；前2~7 d滑动平均的最大气象负荷与当日最大气象负荷的相关性逐渐减小。因此，在建立预报模型时，将前1 d最大气象负荷作为重要的预报因子。

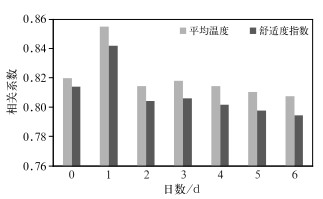
为进一步研究累积气象因子与气象负荷的影响，将累积气象因子定义为当日(0 d)与前1~6 d气象因子的滑动平均，并分别计算与当日气象负荷的相关系数(图 4)。根据前文分析，最大气象负荷与温度的相关性最高，本文选取平均温度为代表，计算其与最大气象负荷之间的相关系数。同时考虑到综合气象因子(舒适度指数)与气象负荷存在较好的相关性，一并计算了其与最大气象负荷之间的相关。可以发现，平均温度与舒适度指数前1 d的滑动平均与当日最大气象负荷的相关性最高，分别达到0.86和0.84；而与其他时段气象因子的平均相关性逐渐减弱，表明夏季最大气象负荷与前1 d平均温度和舒适度指数的变化最显著、敏感性最高。因此，建立最大气象负荷预测模型时，可将前1 d平均气象因子最为预报因子。

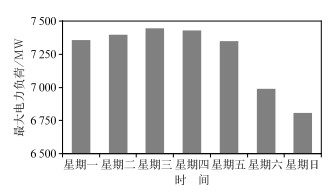
图 5给出了2016 —2018年武汉夏季最大电力负荷的周变化曲线，可以看出工作日的平均最大电力负荷比周末高6.5%~7.9%，说明武汉夏季最大电力负荷的周末效应明显。为分析周末效应在预报模型中的影响，分别建立预测模型，从预测结果看出，工作日和周末的预测误差在0.5%左右，差别不大。即，实况中武汉夏季最大电力负荷的周末效应较明显，但在预测模型中，周末效应相对较弱。因此，工作日与周末基础电力负荷的差异可能并不是造成两者最大电力负荷预测精度存在差异的主要原因(李琛等，2019)。在下文分析中，使用工作日和周末一起建立预报模型。

3 预测模型建立

根据上文分析，选取2016 —2017年前1 d最大气象负荷、前2 d平均的最高温度、最低温度、平均温度、相对湿度、日照时数共六个要素作为预报因子(模型1)，分别利用逐步回归和双隐含层BP神经网络方法，建立最大电力负荷预报模型(在气象负荷预测结果中叠加变化趋势项)，并利用2018年夏季的数据进行预测检验。

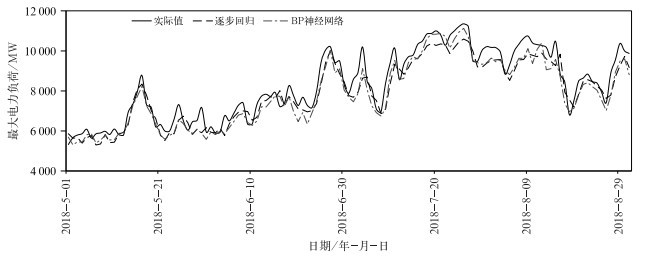
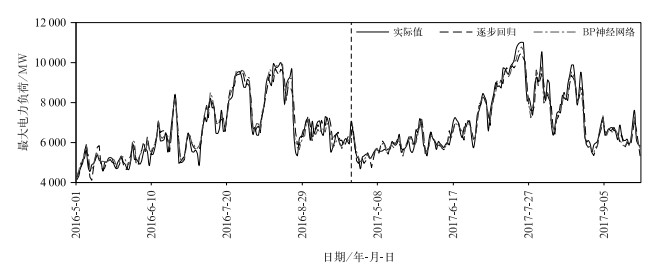
图 6为2016 —2017年武汉夏季最大电力负荷的回代计算结果。可以看出，逐步回归和BP神经网络算法可较好地拟合出武汉夏季最大电力负荷的变化特征。两种方法建立的预测模型较好地模拟了武汉夏季最大电力负荷逐渐增加的趋势；同时对日最大电力负荷的波动变化也有准确的刻画，武汉夏季最大电力负荷一般出现在温度最高的7月20日至8月10日前后。从预测误差结果看(表 2)，BP神经网络预测误差在5%以内占比为71.9%，逐步回归占比为61.8%，BP神经网络预测准确率高于逐步回归；预测误差在2%以内的占比结果也有类似的结论。可见，根据逐步回归和BP神经网络方法建立的预测模型，对2016 —2017年武汉夏季最大用电负荷具有较好的模拟能力。但从平均相对误差、最大相对误差、相关系数和均方根误差看，BP神经网络建立的预测模型要好于逐步回归。

图 7给出了2018年武汉夏季最大电力负荷的预测结果。可以看出，逐步回归和BP神经网络方法构建的预测模型可较好地模拟2018年武汉夏季最大电力负荷的变化特征。相对误差在5%以内的占比分别为43.0%和41.2%，相对误差在2%以内的占比为15.0%和16.9%。由于2018年夏季武汉遭受多轮极端高温天气，对电网最大电力负荷的变化产生显著的影响。这也是造成对2018年夏季最大电力负荷预测准确率较2016年和2017年相对低的原因。2018年7月15日至8月15日，最高温度大于35℃的天数达到24 d，其中7月15日至8月3日最高温度连续突破35℃，极端最高温度达38.6℃。受持续长时段高温的影响，武汉最大电力负荷一直处于高位运行，从7月16日开始最大电力负荷突破10000 MW，7月26日达到极大值11350 MW，一直持续到7月27日最大电力负荷连续在10000 MW以上运行。7月30日至8月2日、8月7—15日两个时段也连续突破10000 MW。两种预测方法对7月15日至8月15日这段高温过程造成的最大电力负荷高位运行的模拟结果较好，平均预测准确率分别在94.0%和95.4%。可见，逐步回归和BP神经网络可以较好地预测2018年武汉夏季最大电力负荷的变化，尤其是对持续高温造成高位运行的最大电力负荷的模拟。

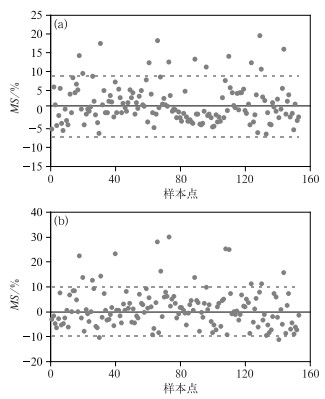
4 敏感性分析

为分析气象因子对电力负荷预测的敏感性，以2018年夏季为主要研究时段，将逐步回归和BP神经网络预测效果进行对比分析，敏感性计算方法如前所述，结果如图 8所示。可以看出，在逐步回归和BP神经网络方法建立的预测模型中，气象因子对最大电力负荷的敏感性(MS)在10%以内占比较大；但MS在10%以上的均对最大电力负荷预测为正的贡献。图 9给出了MS在不同区间的分布情况，MS_SR为正的10%以内的占比为35.3%，负的10%以内的占比为56.2%，表明在逐步回归方法建立的预测模型中，MS在10%内气象因子正的贡献要小于负的贡献。MS_BP为正的10%以内的占比为42.5%，负的10%以内的占比为40.5%，表明在BP神经网络方法建立的预测模型中，MS在10%内气象因子正的贡献要高于负的贡献。

但是，值得注意的是，MS高于10%的情况又是如何？而这往往是影响电力负荷预测的关键时段。从图 8和图 9可以看出，MS在10%以上的占比，MS_SR为8.5%，MS_BP为9.2%；表明敏感性在10%以上时，气象因子对电力负荷预测均为正的贡献。

为进一步说明气象因子对电力负荷预测的影响，选取了敏感性最大的前6个样本，分别给出了最大电力负荷实况、预测及对应的气象要素(表 3)。从统计结果可以看出，9月6日受降水影响，温度出现明显下降，最大负荷较前1 d下降了1680 MW，降幅为17.9%。在考虑了联合预测因子的模型1中，逐步回归和BP神经网络方法的预测准确率分别为96.8%、89.9%。但在仅考虑了气象负荷因子的模型2中，逐步回归方法的预测准确率仅为78.5%，而BP神经网络方法的预测准确率为83.3%，预测准确率远低于模型1；其他样本中存在类似的特征。可见，气象因子在电力负荷预测作为重要的因子，不容忽视。

为进一步探讨联合气象因子对负荷预测的影响，引进人体舒适度作为预测因子(模型3)得出的2018年夏季最大电力负荷，结果如表 4所示。模型2中，逐步回归和BP神经网络预测相对误差在5%以内的占比分别为50.9%和45.8%，在2%以内的占比分别为24.2%、18.9%；但模型3中，逐步回归和BP神经网络预测的最大负荷相对误差分别小于5%和2%的占比远小于模型2，其他参数也存在类似的特征，表明，单独以历史气象负荷为预报因子比以舒适度为预报因子对电力负荷预测影响更为显著。

5 结论与讨论

利用2016 —2018年武汉夏季最大电力负荷数据及同期气象资料，基于逐步回归和BP神经网络算法，开展了武汉夏季最大电力负荷的预测研究，同时进行了气象因子对电力负荷预测的敏感性分析，主要结论如下：

(1) 去除了长期变化趋势后，武汉夏季气象负荷与平均气温、最高气温、最低气温及舒适度指数的相关性明显增强，相关系数提高了20%~40%；在进行夏季日最大电力负荷预测研究中，用分离后的气象负荷代替原始最大电力负荷。

(2) 气象负荷与温度呈显著的正相关关系，与平均温度、最高温度、最低温度的相关系数分别为0.78、0.76、0.64；日照时数与气象负荷也存在稳定的正相关关系。当日最大气象负荷与前1 d最大气象负荷的相关性最大；前2~7 d滑动平均的最大气象负荷与当日最大气象负荷的相关性逐渐减小。平均温度与舒适度指数前1 d的滑动平均与当日最大气象负荷的相关性最高，而与其他时段气象因子的平均相关性逐渐减弱。

(3) 从2016 —2017年回算结果看，逐步回归和BP神经网络预测的最大电力负荷可以较好地拟合出实际值的变化特征。两者方法建立的预测模型较好地模拟了武汉夏季最大电力负荷逐渐增加的趋势；同时对日最大电力负荷的波动变化也有准确的刻画。从2018年预测结果看，两种方法可较好地模拟2018年武汉夏季最大电力负荷，但预测准确率要低于2016 —2017年回算结果。

(4) 气象因子对最大电力负荷MS_SR为10%以内的占比为35.3%，负10%以内的占比为56.2%；MS_BP为正的10%以内的占比为42.5%，负的10%以内的占比为40.5%。MS在10%以上的占比，MS_SR为8.5%，MS_BP为9.2%；表明敏感性在10%以上时，气象因子对提高电力负荷预测精度为正的贡献。

本文在研究中，采用去除夏季最大电力负荷的线性趋势的方法，来分离出气象负荷，但这很难完整地剔除城市基础电力负荷，这是本文的不足之处，也是以后研究的重点。尽管对2018年7月15日至8月15日这一持续高温过程中最大电力负荷的预测结果较好。但由于电力负荷变化规律的复杂性，叠加夏季复杂的天气过程，对最大电力负荷转折时间及持续时段的把握，依然是未来电力负荷预测的难点，这一过程必然离不开气象因子的贡献。未来需进一步深入挖掘气象因子对电力负荷预测的敏感性，借助深度学习、大数据分析、人工智能等先进方法，提高模型的预测精度，切实为电网调度安全运行提供气象保障。