引言

自动雨量站能够准确获得单点的降水强度和一段时间的累积降水量，截至2019年底，气象部门已经在全国建成约8万多个(http://data.cma.cn)自动雨量站用于业务观测，包括国家级自动站和区域自动站。自动站的观测资料具有分布范围广，时空分辨率高，传输及时等特点，在气象业务和服务中得到广泛应用。然而，自动雨量站也存在着一定的问题，如：雨量的测量受风场影响较大，尤其是翻斗式雨量计在大雨情况下由于翻斗来不及翻动造成雨量流失而使得观测值有较大误差；树叶污泥等遮挡、杂物堵塞、人为浇水、破坏以及维护不当等因素均可以造成雨量测量的误差(Habib et al, 2001；Yeung et al，2010)。因此，在定量使用自动站观测的降水数据之前，需要对其进行质量控制。

美国和北欧在雨量计数据质量控制方面走在前列，其相关的质量控制方法具有较强的代表性。美国为了应对不同数据部门的应用需求，如分别针对河流预报中心(RFCS)、水文数据系统(HADS)以及天气预报中心(WFOS)等部门，分别开发了三套较为典型的自动雨量站数据质量控制系统：(1)美国国家气候中心(NCDC)根据雨量站的位置和降水过程的时间及空间一致性(空间相关：0.5°，时间相关：1 h)开发了一套基于极端值点去除的方法(Kim et al，2009)。但是该方法较易误剔除一些真实的强降水站点值；(2)地球系统研究实验室(ESRL)根据日值和月值的气候统计变化的分析结果，专门针对日降水观测量进行数据质量控制(Tollerud et al，2005)；(3)美国强风暴实验室(NSSL)将其Q2系统下基于卫星、雷达、多种地面观测设备等多源数据融合的小时降水率拼图产品应用于自动雨量计的数据质量控制中(Rissanen et al，2000; Vejen et al，2002)。这些方法基本都是建立在认为某一空间范围内要素的分布均一的假设上，比较适合压强、温度、湿度要素的质量控制，而对于降水则有较大的局限性。我国对于地面自动雨量计观测资料已经制定了三级质量控制业务规范(任芝花和熊安元，2007)，利用常规格式检查、极值检查、空间一致性检查等对自动站的观测资料进行质量控制，但是在雨量计的随机误差中，由于机械故障、人为浇水等原因造成的污染数据，往往通过极值检查较难处理。为了解决极值法的局限性，任芝花等(2010)利用降水数据的时空一致性对全国区域自动站和国家级自动站实时上传数据资料进行质量控制。这种方法对于单纯的极值法是一种进步，但是对于周围雨量计较少的情况则有其局限性。王红艳等(2015)结合雷达资料，利用两步校准法建立雷达定量降水估测数据，对雷达QPE数据与雨量计观测数据之间的差异进行统计分析，确定自动雨量计质量控制的一些方法和标准，能够较好地在时空一致性上对自动雨量计进行质量控制。

目前，随着双偏振天气雷达升级进程的加速，以及双偏振天气雷达在云降水领域的广泛应用，在定量降水估测方面的精度进一步提高，对建立自动雨量计质量控制的规则及阈值带来更大的确定性(陈超等，2019)。本文利用海南省500多个自动雨量计及海口双偏振天气雷达对2019年第7号台风韦帕连续7 h的降水观测资料，采用空间一致性检测[反距离权重法(IDW)]和观测一致性检测[雷达定量降水估测值(QPE)]的质量控制方法，综合考虑天气过程的空间一致性及观测一致性，建立一套自动雨量计的综合质量控制方法。

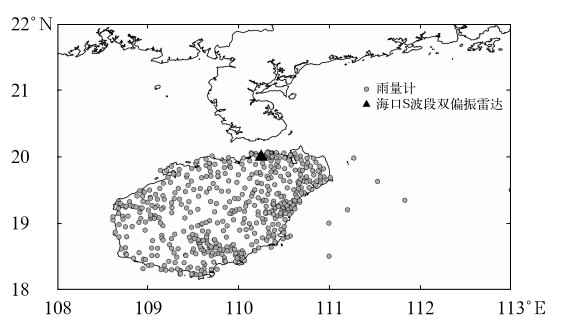
1 资料

本研究使用海南省500多个自动雨量站(国家级自动站和区域自动站)，自动雨量站资料为逐小时雨量数据，其降水量分辨率为0.1 mm；以及海口S波段双偏振天气雷达数据。雷达及雨量计的分布情况如图 1所示。

海口S波段多普勒天气雷达属于中国新一代天气雷达，并于2017年初实现了双偏振升级，资料格式、探测模式等参数均采用标准的VCP21D降水观测模式，体扫时间间隔为6 min扫描11个仰角，在常规雷达观测的基础上增加了差分反射率因子(Z_DR)、差分传播相移(φ_DP)和零滞后相关系数(ρ_HV)的观测，距离分辨率由1 km提升到了250 m。为了更好地使用偏振雷达观测数据，需要对雷达进行相应的标定及雷达基数据的预处理，其处理过程如下：

(1) 在对雷达Z_DR系统偏差校准方面，使用微雨法利用回波强度在15~25 dBz的小雨回波进行系统Z_DR偏差订正，小雨回波的Z_DR理论值在0 dB左右，Z_DR观测值与理论值之间的差异即为Z_DR系统偏差；

(2) 反射率因子(Z_H)和Z_DR使用中值滤波器以及沿径向上5个距离库的滑动平均值的方法来消除异常值和减少随机波动；

(3) 根据ρ_HV < 0.85的阈值来剔除地物杂波、湍流散射、异常杂波等非气象回波；

(4) 为了准确估测差分传播相移率(K_DP)，首先，根据地物杂波的差分相位均值来标定系统的初始相位，然后再平滑滤波，最后通过线性编程的方法来计算K_DP(Huang et al, 2016)同时确保K_DP值的非负性。

本文使用2019年第7号台风韦帕降水过程为例，在大面积强降水过程中，研究自动雨量计数据综合质量控制方法，分析验证质量控制效果，以获得适用于海南省自动雨量站数据质量控制的有效方法和规则。本文选用2019年8月1日02—08时(北京时)台风过程中海南省境内出现大面积降水的过程作为研究对象，其降水信息统计结果如下表 1所示。

其中有降水记录站点个数表示平均每小时累积降水量大于0 mm的站点个数，雨量计总数表示平均每小时参与质量控制的雨量计总数。有效降水平均强度表示平均每小时雨量计小时雨量大于0 mm的站点的雨强平均值。

2 综合质量控制法

联合天气雷达定量降水估测(QPE)对雨量计进行数据质量控制，基于空间一致性和观测一致性的综合质量控制方法。空间一致性检测根据待测站点周围雨量计的观测值计算其估计值，并统计分析待测站点观测数据的可疑性；观测一致性检查使用雨量计上空雷达QPE(订正后)与雨量计观测值进行对比分析，对可疑雨量计进行二次确认。综合质量控制算法流程如图 2所示。

2.1 空间一致性质量控制

对于区域降水而言，每个参与测量的雨量计之间应存在一定的相关性，距离越近的雨量计之间的相关性越强(刘雨佳等，2014)，自动雨量计的空间一致性质量控制就是利用这种相关性，找出表现异常的站点。由于降水具有较强的时空不均匀性，对降水数据进行空间一致性质量控制时，应尽量选取距离较近的站点。

反距离权重(IDW)插值法按照距离赋予周边站点不同的权重，目标站点雨量估测值计算表达式如下：

$ G_{\mathrm{e}}=\frac{\sum\limits_{i=1}^{n} G_{\mathrm{m}(i)} W_{i}}{\sum\limits_{i=1}^{n} W_{i}} $

(1)

$ W\left(d_{i}\right)=\left\{\begin{array}{ll} 1 / d_{i} ~~~~~~~~ 0<d_{i} \leqslant R / 3 \\ (27 / 4 R)\left[\left(d_{i} / R\right)-1\right]^{2} ~~~ R / 3<d_{i} \leqslant R \\ 0 ~~~~~~~~ d_{i}>R \end{array}\right. $

(2)

$ \Delta=\frac{\left|G_{\mathrm{e}}-G_{\mathrm{m}}\right|}{\sigma} $

(3)

式中：G_e为目标站点的反距离权重估测雨量值，G_m为目标站点的观测雨量值，G_m(i)表示目标站点周边雨量计的观测值；W(d_i)表示周边第i个雨量站的权重系数，周边雨量计距离目标雨量计越近，权重越大(Chen et al, 2015)；d_i表示目标雨量站与周边雨量站的距离(单位：km)，其中R为搜索半径(单位：km)；σ取距离最近12个雨量计观测值与估计值之差的标准差(勾亚彬等，2014)，其权重随距离的变化如图 3所示。

考虑到局部区域内的雨量计相对稀疏以及较远处观测资料对目标站点的代表性相对较差(勾亚彬等，2014)，周边雨量计的搜索半径(影响范围)设置为10 km。通过对比式(3)的计算结果与事先设定的阈值，对目标雨量计进行质量控制。一些经验性的阈值设置根据3倍标准差的判断准则(莱以特准则)，选择Δ的阈值为3。如果雨量计分布稀疏或者雨量计站点无降水数据，则有可能σ很小甚至为0，导致Δ很大引起错误的判断。此时，有必要进一步考察目标站点的估测雨量(G_e)与观测雨量(G_m)的相对误差及绝对误差。考虑到降水系统空间分布的不均匀性，及自动观测资料空间采样的不确定性，需结合相对误差和绝对误差进行判断。降水较弱的雨量计站点主要考虑绝对误差，降水较强的雨量计站点主要使用相对误差为判断依据。目标站点数据是否可疑的具体标准为：当目标站点的观测雨量小于一定的阈值(本文设定10 mm)，则使用绝对误差阈值进行检验(本文设定2.5 mm)，当目标站点的观测雨量大于设定阈值，则使用相对误差进行检验(本文设定30%)。

2.2 基于CSU-HIDRO最优化雷达定量降水估测

双偏振雷达定量降水估测CSU-HIDRO优化算法是由美国科罗拉多州立大学Cifelli et al(2011)提出的。该算法主要是在模糊逻辑法水凝物分类的基础上(冯亮等，2018)，根据不同的降水类型及K_DP、Z_H、Z_DR的阈值选择不同的降水率计算公式。其算法流程如图 4所示，图中的关系如式(4)~式(7)所示。

$ R\left(Z_{\mathrm{H}}\right)=a_{1} Z_{\mathrm{H}}^{b_{1}} $

(4)

$ R\left(K_{\mathrm{DP}}\right)=a_{2} K_{\mathrm{DP}}^{b_{2}} $

(5)

$ R\left(Z_{\mathrm{H}}, Z_{\mathrm{DR}}\right)=a_{3} Z_{\mathrm{H}}^{b_{3}} 10^{c_{3}z_{\mathrm{DR}}} $

(6)

$ R\left(K_{\mathrm{DP}}, Z_{\mathrm{DR}}\right)=a_{4}\left(K_{\mathrm{DP}}\right)^{b_{4}} 10^{c_{4}z_{\mathrm{DR}}} $

(7)

式中：R为降水率(单位：mm·h^-1)，Z_H为反射率因子(单位：mm⁶·m^-3)，Z_DR为差分反射率因子(单位：dB)，K_DP为差分传播相移率(单位：°·km^-1)。

由于降水率与偏振量参数之间的关系受雨滴谱变异性的影响较大(Tang et al, 2014)，因此，本文利用安装在海口站的雨滴谱仪收集到的雨滴谱数据(“韦帕”台风过程)。使用非球形粒子的散射模型(T-Matrix)和观测到的雨滴谱数据对S波段雷达的偏振量进行模拟(Zhang et al, 2001)，结合滴谱数据信息计算其降水率，拟合出各表达式中的参数，以减小由于滴谱变异性所带来的误差。拟合参数如表 2所示。

2.3 雷达定量降水估测校准订正

双偏振雷达定量降水估测采用最低仰角(0.5°)偏振量观测数据，由2.2节的降水估测算法反演各时次的瞬时雨强，采用时间线性平均法(李建通等，2005)逐点累积得到定量降水估测初始降水场。为了降低雷达定量降水估测的系统误差，联合质量控制后的雨量计数据(空间一致性质量控制)，采用薄板样条(TPS)插值法(杜国明和贾良文，2009)对偏振雷达定量降水估测的初始降水场进行校准订正，以降低偏振雷达定量降水估测的系统误差(东高红和刘黎平，2012；李建通等，2015)。

双偏振雷达QPE校准订正过程如下：首先，利用空间一致性质量控制后的雨量计观测数据与雨量计上空雷达定量降水估测值形成匹配数据对，数据的匹配采用雷达降水估测数据向地面进行投影与分辨率内的雨量计进行匹配(郭佳等，2020)，要求匹配数据对中的降水数据均非零，其比值作为订正因子。然后，利用TPS法对比值进行内插，得到整个雷达观测范围内的订正因子。最后，雷达定量降水估测值乘以订正因子，得到校准后的雷达定量降水估测值。

2.4 观测一致性质量控制

观测一致性质量控制主要是针对经过空间一致性质量控制后被认为是可疑的雨量计站点数据。建立可疑雨量计数据与雷达定量降水估测值(订正后)之间的配对关系，通过分析雨量计观测值与雷达估测值之间的统计误差对可疑自动雨量计进行二次判定。

与2.1中的方法类似，使用相对误差与绝对误差相结合的统计分析方法进行判断，相对误差及绝对误差定义如下所示。

$ R E=\left\{\begin{array}{ll} \frac{R_{\mathrm{g}}-R_{\text {Corr } R}}{R_{\mathrm{g}}} \times 100 \% & R_{\mathrm{g}} \geqslant R_{\text {CorrR }} \\ \frac{R_{\text {CorrR }}-R_{\mathrm{g}}}{R_{\text {CorrR }}} \times 100 \% & R_{\mathrm{g}}<R_{\text {CorrR }} \end{array}\right. $

(8)

$ ABS=|R_{\rm g}-R_{\text {CorrR }}| $

(9)

式中：R_g为自动雨量计小时降水量观测值，R_CorrR为雷达小时降水估测值(订正后)，RE为相对误差，ABS为绝对误差。由于降水强度的不同，RE和ABS表现差异较大。在降水较弱时，相对误差的波动较大，使用相对误差容易出现误判; 相反，在强降水时，自动雨量计与雷达降水估测值之间的绝对误差波动较大，使用绝对误差则误判较多。因此，算法需要综合考虑强弱降水的不同情况。一些经验性的阈值设定，例如，本文设定绝对误差的判定阈值为2.5 mm，相对误差的判定阈值为30%，区分强弱降水的判定阈值为10 mm·h^-1。当雨量计观测值小于10 mm·h^-1，采用绝对误差进行判定，当雨量计观测值大于10 mm·h^-1，采用相对误差进行判定。其主要目的是在剔除差别较大观测数据的同时，允许空间差异在一定范围内的观测数据。考虑到业务应用的推广及算法优化的需要，这些算法阈值设置为可调阈值，以便今后进一步对这些阈值进行优化验证。

3 质量控制效果检验分析 3.1 空间一致性质量控制效果检验与分析

利用2019年台风韦帕8月1日02—08时时段数据对质量控制效果进行检验，此时段内台风韦帕在海南省形成大面积强降水。

根据第2节关于空间一致性的质量控制方法，使用待测站点周围10 km范围内的雨量计计算其估测值，并计算周围雨量计观测值的标准差σ。根据待测站点的估测值、观测值及周围雨量计观测值的标准差σ之间的统计分析结果判断其可疑性。根据统计分析的结果，将可疑站点分为以下三类：第一类：周围10 km范围内无雨量计的待测雨量计站点；第二类：周围雨量计数目过少(使用5个站作为阈值)且观测值与估测值之间的相对误差、绝对误差均不在合理范围内(相对误差阈值为30%，绝对误差阈值为2.5 mm)的待测雨量计站点；第三类：观测值与估测值之差的绝对值大于3倍标准差σ的待测雨量计站点。

由于空间一致性质量控制对于待测站点周围雨量计数目的依赖程度较大。因此，还不能直接将可疑站点认定为错误站点，需要观测一致性质量控制的二次确认。空间一致性质量控制方法主要是允许观测资料在空间上存在一定差异的同时，挑选出差别较大的观测资料视为可疑，以期在后续的质量控制方法中进行二次确认，同时又有利于后续雷达定量降水估测值的校准订正。

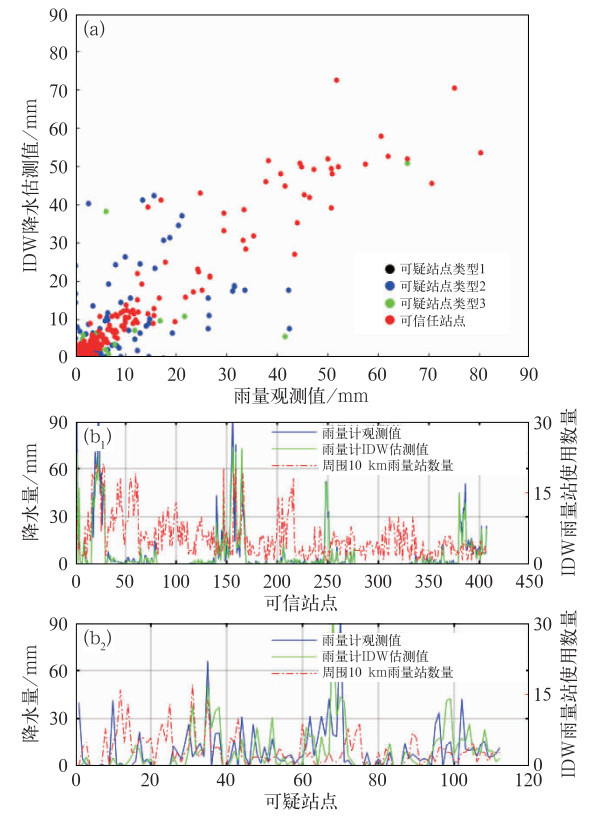
图 5给出了2019年8月1日05—06时雨量计数据空间一致性质量控制后可疑站点与可信站点的观测值、估测值的散点分布及整体趋势的对比分析结果。图 5a给出了各类可疑站点、可信站点观测值与估测值的散点分布。根据三种类型可疑站点的散点分布情况可知，第二类可疑站点的数量分布较多，由于雨量计在局部区域的分布不均，待测站点周围雨量计相对较少，导致IDW估测结果不确定性增大，待测站点观测数据的可疑性增大所致。第一类可疑站点的数量相对较少，主要是使用了大量的雨量计站点(国家站和区域站)，因此，待测站点周围10 km范围内完全没有雨量计存在的情况相对较少，与实际情况较为吻合。第三类可疑站点主要是估测值与观测值偏差较大的站点，其为错误站点的概率也相对较高。

图 5b给出了可疑站点、可信站点的观测值、估计值和周围10 km站点数量的整体趋势，从图中可知，可信站点的观测值与估计值的整体趋势更为吻合，且周围雨量计的分布数量相对更多。相反，可疑站点的观测值与估计值的整体趋势差异较大，其周围雨量计的分布数量相对偏少。说明，空间一致性质量控制法对雨量计的分布状况有较大的依赖性，对于雨量计分布较为稀疏的局部区域容易出现误判。因此，需要有其他的质量控制方法对其中可疑站点进行二次判定。

3.2 双偏振雷达定量降水估测及校准结果分析

根据2.2节中双偏振雷达定量降水估测CSU-HIDRO优化算法，反演从2019年8月1日02—08时，雷达各时次体扫的瞬时雨强，并逐点、逐小时累积得到雷达定量降水估测初始降水场。使用经过空间一致性质量控制后认为是可信数据站点的雨量计与雷达定量降水估测初始降水场进行配对，采用薄板样条插值法(TPS)对雷达定量降水估测值进行校准订正。图 6给出了校准前后，雷达小时降水估测值与雨量计小时观测雨量分布对比(图 6a，6b)，及雨量计小时雨量与雷达小时降水估测值配对数据的散点分布图(图 6c)，降水时次为2019年8月1日04—05时。从图 6a和6b中可以发现，校准前，雷达小时降水估测值总体上相对于雨量计观测值偏小，尤其在强降水区域低估更为明显；校准订正后，雷达降水估测低估现象明显改善。根据图 6c的散点分布结果可知，校准订正前，雷达小时降水估测值在总体趋势上同雨量计观测值较为吻合，但是也存在以下两个问题：(1)雷达小时降水估测值在雨强较大时存在低估，降水越强低估越明显；(2)在雨量计观测值为0 mm的站点处出现了雷达降水估测值高于0 mm的情况。由于此图例中使用了所有的雨量计数据，未经过空间一致性质量控制。因此，这些雨量计处于雨带边缘的可能性较大。校准订正后，雷达小时降水估测值精度更高，订正前的低估现象得到较大改善。但是，对于雨量计无降水而雷达降水估测值大于0 mm的情况基本没有得到改善。如果单独使用观测一致性质量控制方法，这些处于降水边缘的雨量计站点极有可能被判定为错误数据站点。由此，选择先进行空间一致性质量控制，在对质量控制后认为是可疑的数据站点进行二次判定的方法能较大程度地规避这样的误判。

3.3 观测一致性质量控制效果检验与分析

观测一致性质量控制法使用可疑数据站点与雷达小时降水估测值(校准订正后)建立配对关系，通过分析配对数据之间的统计误差，最终确定雨量计站点的可疑性。

使用空间一致性质量控制后判定为可疑数据的雨量计站点进行观测一致性质量控制，如果能够通过联合雷达QPE的观测一致性质量控制，并判定为可信数据，则解除其在空间一致性中的可疑性。否则，待测雨量计最终被认定为错误(存在故障)站点。图 7给出了2019年8月1日03—08时雨量计数据经过观测一致性质量控制后，错误站点、可信站点观测值与雷达降水估测值的散点分布和整体趋势的对比分析结果。根据站点数据的观测值及估测值散点图(图 7a)，可以发现，经过观测一致性质量控制后，多数雨量计站点的可疑性被解除，少量的雨量计依然可疑，最终被确认为错误站点数据。同时存在较多雨量计观测值为0 mm而雷达降水估测值高于0 mm的情况，说明在雨量计分布稀疏的情况下，此方法对于降水边缘的雨量计站点可能存在一定的误判。同时，根据各类雨量计站点的观测值与雷达估计值的分布趋势(图 7b)。表明，错误站点的观测雨量与雷达降水估测值(订正后)偏差较大，其为错误站点数据的可能性较高。

最后，本次降水过程各时次雨量计站点数据经过综合质量控制后的统计结果如下表 3所示。根据最后的错误数据站点率，全过程各时次的错误站点率在5%以下，说明雨量计站点数据较为可靠。综合质量控制方法判定出的错误站点可信度较高。

4 结论与讨论

本文采用雨量计联合双偏振天气雷达QPE对雨量计数据进行质量控制，分别从空间一致性和观测一致性两个角度对雨量计进行综合质量控制。结合海南省海口市业务应用的S波段双线偏振雷达及海南省自动站网数据，使用2019年第7号台风韦帕降水过程对综合质量控制方法进行验证，并得出如下结论：

(1) 单独使用空间一致性质量控制法会出现大量的误判，主要是由于小尺度局部强对流的存在，使得小区域的降水值偏高，同时这个区域的雨量计分布稀疏时将形成较多误判。需要结合雷达定量降水估测的观测一致性质量控制方法，以此排除这样的误判。

(2) 在进行空间一致性质量控制过程中，待测站点周围雨量计的数量及距离对判定结果的影响较大，离待测站点距离较近的雨量计越多，其判定结果越准确，反之亦然。

(3) 双偏振雷达定量降水估测的初始降水场经过薄板样条(TPS)插值法校准订正后具有较高的精度，对观测一致性质量控制起到较好的正向作用。

(4) 本次降水过程共计6 h，整体错误站点率在5%以下，说明雨量计站点的可信度较高。同时，部分错误站点是由于其观测雨量值为0 mm而雷达降水估测值非零所致，可能是由于雨量计分布稀疏且同时处于降水带边缘造成。

利用双偏振雷达QPE对雨量计进行数据质量控制，可以提醒设备维护人员对雨量计进行及时的检查和维护，以提高雨量计数据在气候研究和气象服务等方面的应用水平。同时，需要说明的是，本文使用的综合质量控制方法也有一定的不足。如在雨量计分布稀疏的情况下，其待测站点周围雨量计相对较少，空间一致性质量控制会判定为可疑。如果这样的雨量计又处于降水边缘，在观测一致性质量控制的过程中，其观测雨量与雷达定量降水估测值存在一定的偏差，最终判定为错误站点。因此，对于这种情况可能存在一定的误判，有待改进。