2. 中国人民解放军93995部队, 西安 710000
2. Unit 93995 of PLA, Xi'an 710000
台风是影响中国的主要灾害性天气系统之一,其登陆后的灾害往往是由台风暴雨引发的(程正泉等,2005), 而暴雨引发的洪涝、泥石流、城市内涝等灾害,可能会对社会经济,人民生命财产安全等造成严重危害。台风降水具有非对称性特征(张亚洲等,2011),其暴雨的强度可能与大尺度环流背景、中尺度系统、局地地形、边界层辐合等许多方面关系密切(周福等,2014),因此有关台风暴雨的研究一直是国内外气象学者们尤为关注的热点和难点问题之一(孙力等,2015)。目前在台风暴雨机理方面有了较多的研究进展。如,丁治英和陈久康(1995)、孙建华和赵思雄(2000),研究发现高空急流入口区右侧的强辐散区对台风暴雨具有加强作用,而其下方台风环流的涡度、散度、温度场等非均匀分布极大地加强了高层热成风,这种高低空配置导致低层强辐合,利于形成台风倒槽,登陆后的台风暴雨位于台风倒槽的强辐合区和台风北侧的暖平流中(陶祖钰等,1994)。Chien and Smith (1977)的研究则强调了潜热释放以及暖平流对热带气旋发展的重要作用,而杨晓霞等(2008)、杜惠良等(2011)的研究也表明持续获得暖湿能量输送可以减缓北上台风的衰减速度,配合弱冷空气影响,可继续引发暴雨。陈联寿等(2017)将台风暴雨区细分为环流内暴雨(眼壁暴雨、螺旋雨带暴雨、小涡暴雨、倒槽暴雨、切变暴雨)及环流外暴雨(台前飑线暴雨、远距离暴雨和变性下游效应暴雨)并总结分析各暴雨区的形成机理;陈联寿和许映龙(2017)分析特大台风暴雨(1 000 mm·d-1)形成原因,发现其与登陆台风停滞时间、不同系统相互作用、山脉地形、台风高层云团中微物理过程密切相关,这些最新的研究结果对台风暴雨业务预报具有重要的参考价值。
天气形势演变为暴雨提供了大尺度背景场,而暴雨的发生则取决于降水的内在物理机制(韩沁哲等,2009),因此可以用一些表征大气动力、热力、水汽的物理参数对暴雨进行物理诊断分析。Q矢量、湿位涡等物理量被广泛应用于诊断台风暴雨分析之中,并取得了一定研究成果(岳彩军,2014)。如许多学者运用非地转湿Q矢量对台风暴雨的诊断分析发现,台风暴雨带位于低层非地转Q矢量散度梯度大值区且靠近辐合区(张亚洲等,2011),而低层非地转Q矢量散度辐合区强度与未来6 h降水强度具有正相关对应关系(姚秀萍和于玉斌,2000;Yao et al,2004;高留喜等,2008;吴星霖等,2008;傅灵艳等,2009)。Hoskins et al(1985)指出湿位涡(MPV)因考虑了水汽作用,与实际台风暴雨生成条件更加接近(曹楚等,2016)。对流层高层湿位涡下传,有利于位势不稳定能量的存储和释放,增强降水的发生(曹楚等,2016;何丽华等,2007;于玉斌和姚秀萍,2000;赵宇等,2004),台风暴雨区位于对流层中低层MPV1负值区与MPV2正值区的叠加区(曹楚等,2016;何丽华等,2007;赵宇等,2004;张建海和庞盛荣,2011;余贞寿等,2010)。
上述这些常用的物理量基本上是基于空间某一或某几个气压层的定性诊断分析,而究竟哪一层对台风暴雨具有强指示意义,该物理量能否预报出暴雨的强度量级等问题仍有待研究。因此基于暴雨形成机理,分析暴雨发生的动力、热力、水汽因子的配合和空间结构演变(韩沁哲等,2009),引入一些关键物理因子,构建可以指示暴雨强度的综合物理诊断量对提升暴雨预报能力具有重要意义,而这一物理诊断量的构建过程即被称为“配料法”(Doswell Ⅲ et al,1996)。配料法的优势在于,针对某种天气现象,选取引起其发生的重要物理量进行组合搭配来预测该天气,利用该方法建立的预报指标具有清晰的物理意义,为预报员提供了一种简单、快捷的预报思路(李德帅等,2016)。“配料法”在国外发展较快,在预报暖季雷暴(Doswell Ⅲ,1987;McNulty,1978)、暴洪(与洪水相关的短时暴雨)(Doswell Ⅲ et al,1996)、冬季降水(Wetzel and Martin, 2001;Schultz et al,2002)等方面均得到了一些可观的成果;近年来,我国学者在基于“配料法”的暴雨预报研究方面也取得了一些成果:来小芳等(2007)、刘勇等(2015)、李德帅等(2016)都采用“配料法”研发了强降水指数,其预报效果均好于单一物理量预报;何钰等(2018)、刘国忠等(2013)、张萍萍等(2012)则基于不同天气类型采用“配料法”研究暴雨预报并取得了较好的预报效果。
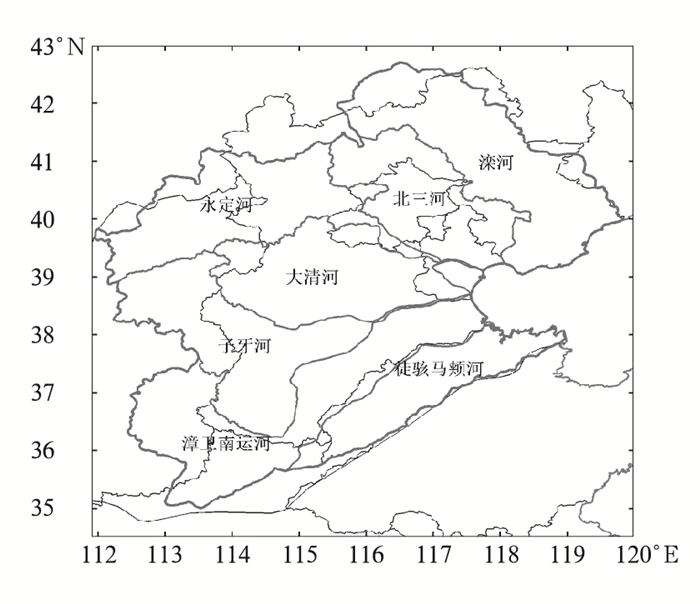
海河流域地处华北平原(图 1),流域河系众多复杂,山区平原过渡期短,遇强降水易产生洪涝灾害。北上台风是汛期影响海河流域产生暴雨的重要天气系统,且进入20世纪末期以来北上台风显著增多(高松影等,2017;史得道等,2014),仅2018年7—8月就有台风安比、摩羯、温比亚三个台风北上直接影响海河流域,造成了流域区域性大到暴雨的天气,增加了流域致洪风险。因此,本文从影响降水的动力、热力及水汽条件入手,注重分析台风暴雨特点,采用“配料法”构建综合物理指数,并用北上台风暴雨个例进行普适性检验,旨在为海河流域北上台风暴雨预报提供一些有价值的参考。
|
图 1 海河流域及河系分区 Fig. 1 Haihe River Basin and its partition |
大气是一种非线性系统,降水的形成与大气环流背景及其物理参数关系十分密切(Kunz,2007),其强降水的发生往往需充足的水汽、不稳定层结和足够的抬升条件,是三者共同作用的结果,但真正发生强降水时,不一定所有的物理量指标都比较大,而是其组合信号较大时,强降水发生概率有所增大,因此对强降水发生前期各物理量的强信号进行处理与挖掘,构建综合物理指数对提升强降水预报能力十分重要。李德帅等(2016)基于动力、水汽、不稳定三者“交集”区域的思路建立的综合THP(temperature, helicity and precipitable water)指数,尽管对于强降水预报有一定预报效果,但是该指数中没有包含垂直运动条件,也并不是对于所有天气系统都适用,通过检验发现THP指数往往会放大北上台风暴雨预报落区(图略)。因此本文采用“配料法”,基于上述取“交集”的构建思路,并侧重考虑台风发生发展的特点,研发一种适用于北上台风强降水预报的综合物理指数,为北上台风强降水预报提供一定的参考。
1.1 不稳定条件大气不稳定条件包括热力不稳定和动力不稳定。
1.1.1 热力不稳定参数热力不稳定也称静力不稳定或层结不稳定,大多数热力不稳定属于“潜在不稳定”,当没有释放机制存在时,这种不稳定没有意义(孙继松和陶祖钰,2012)。强风暴发生前往往有不稳定能量的聚集,而发生时不稳定能量将得到迅速释放。本文选取的热力不稳定参数为李德帅等(2016)研究的热力不稳定参数假相当位温(θse)通量散度之差Γ,该参数是根据干、湿绝热过程的假相当位温(θse)守恒性(朱乾根等,2007)推导出来的。Γ具体表达式为
| $ \begin{array}{l} \mathit{\Gamma} = \frac{\partial }{{\partial t}}\left( {\frac{{\partial {\theta _{{\rm{se}}}}}}{{\partial p}}} \right) = \frac{\partial }{{\partial p}}[ - {\nabla _h} \cdot ({\theta _{{\rm{se}}}}{\mathit{\boldsymbol{V}}_h})]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{\nabla _h} \cdot {{({\theta _{{\rm{se}}}}{\mathit{\boldsymbol{V}}_h})}_{{\rm{high}}}} - {\nabla _h} \cdot {{({\theta _{{\rm{se}}}}{\mathit{\boldsymbol{V}}_h})}_{{\rm{low}}}}}}{{{p_{{\rm{high}}}} - {p_{{\rm{low}}}}}} \end{array} $ | (1) |
该热力不稳定度参数具有明确的物理意义,θse通量散度[
从运动学的观点来看,旋转的流体有利于能量的维持,对风暴的发展与维持起到了积极作用。在对流层低层几千米内(一般指3 km),相对于风暴的风向随高度顺转是风暴旋转发展的关键因子,风暴相对螺旋度H表征垂直风切变环境中风暴运动所产生的旋转潜势,是一种表征对流系统动力不稳定性的重要参数,其具体公式为
| $ \begin{array}{l} H = \int_0^h {({\mathit{\boldsymbol{V}}_h} - \mathit{\boldsymbol{C}}) \cdot {\mathit{\boldsymbol{\omega }}_k}{\rm{d}}z} = \\ \sum\limits_{n = 0}^{N - 1} {[({u_{n + 1}} - {c_x})({v_n} - {c_y}) - ({u_n} - {c_x})({v_{n + 1}} - {c_y})]} \end{array} $ | (2) |
式中:Vh=(uz, vz)为各高度层上环境水平风场;C=(cx, cy)为风暴移动速度;ωk=k×dVh/dz为水平涡度矢量, k为z方向的单位矢量;h为气层厚度,N为计算时取环境风的层次。实际计算时,选取850~400 hPa平均风风向向右偏转40°、风速的75%(李德帅等,2016)作为该点的风暴移动速度。积分层次N取NCEP资料925~650 hPa的等压层,共7层:925、900、850、800、750、700和650 hPa。
1.2 水汽与动力条件降水产生的直接原因是由充足的水汽和垂直运动共同作用的结果,而水汽凝结量既是水汽辐合上升的结果产物,又是产生降水直接物质来源。因此,文中引入单位时间的水汽凝结量即水汽凝结率(WC)作为综合诊断水汽和垂直运动的物理参量,推导过程如下:
假设单位时间内,一个底边长为ΔL、高为ΔZ的立方体中水汽凝结率为
| $ WC = - \rho \frac{{{\rm{d}}{q_s}}}{{{\rm{d}}t}} \cdot \Delta L \cdot \Delta L \cdot \Delta Z $ | (3) |
将静力平衡公式ΔZ=-Δp/ρg代入到式(3),整理后得到:
| $ WC = \frac{1}{g}\frac{{{\rm{d}}{q_s}}}{{{\rm{d}}t}} \cdot \Delta {L^2} \cdot \Delta Z $ | (4) |
若取上式中物理量单位:g:cm·s-2; qs:g·kg-1; L:cm; p:hPa=kg·cm-1·s-2, 则计算得到水汽凝结率的单位为g·s-1。
取底边边长ΔL=1 cm, 截面高Δp=-1 hPa,则单位体积内的水汽凝结率为
| $ WC = - \frac{1}{g}\frac{{{\rm{d}}{q_s}}}{{{\rm{d}}t}} $ | (5) |
单位为g·s-1·cm-2·hPa-1。
引入凝结函数
| $ \frac{{{\rm{d}}{q_s}}}{{{\rm{d}}t}} = F\omega $ | (6) |
式中:ω为垂直速度。
由于只有湿空气上升达到饱和时才会发生凝结,所以引入系数δ,则
| $ \frac{{{\rm{d}}{q_s}}}{{{\rm{d}}t}} = \delta F\omega $ | (7) |
式中:当q≥qs且ω<0时,δ=1;否则δ=0。
将式(7)代入式(5),则单位体积内水汽凝结率
| $ WC = - \frac{\delta }{g}F\omega $ | (8) |
由于凝结函数F恒大于0(朱乾根等,2007),而ω<0才有意义,所以上式恒大于0。
从式(8)可以看出,水汽凝结率可以综合反映湿绝热系统的垂直运动、水汽以及凝结潜热释放热信息。而台风的发展维持是大尺度运动与积云对流相互作用的结果,即积云对流释放的凝结潜热提供驱动大尺度运动所需的热能,而大尺度扰动又产生发生积云对流所需的湿空气辐合(朱乾根等,2007)。可见在台风北上过程中,如果没有明显的北方冷空气侵入或者冷空气很弱的情况下,则潜热释放在其维持发展中仍起到不可缺少的作用。故包含潜热释放信息的水汽凝结率作为台风暴雨的一个重要诊断参数具有一定合理性。构建指数时,取整层最大水汽凝结率(WCmax)进行计算,即
| $ W{C_{{\rm{max}}}} = {\left( { - \frac{\delta }{g}F\omega } \right)_{{\rm{max}}}} $ | (9) |
本文采用“配料法”,取降水发生三要素:动力、水汽、不稳定的“交集”进行构建,将热力不稳定参数即θse通量散度差、动力不稳定参数即风暴相对螺旋度H、动力与水汽综合参数即最大水汽凝结率进行组合,得到新型强降水指数THWC(temperature, helicity and water condensation),为避免负号带来的影响,构建指数时取各物理参数的绝对值进行构建,即
| $ THWC = \left| \mathit{\Gamma} \right| \times \left| H \right| \times \left| {{W_{{\rm{cmax}}}}} \right| $ | (10) |
本文所使用的降水实况资料来自于中国气象局下发MICAPS系统逐小时加密自动站资料。首先将逐小时加密自动站降水量资料处理为08—14、14—20、20—02和02—08时逐6 h累积降水量资料,并采用Cressman方法将流域内(32°~43°N、112°~120°E)降水站点资料插值到0.05°×0.05°网格点上。
本文所用的再分析资料来自于美国国家环境预报中心及大气研究中心(NCEP/NCAR)6 h间隔再分析资料,包括500 hPa位势高度场、水平风速场(u, v)、垂直速度场(w),相对湿度场以及温度场。其中所用再分析资料集为NCEP-GFS(ds083.4)数据集(https://rda.ucar.edu/datasets/ds083.3/index.html),其空间分辨率为0.25°×0.25°,数据长度为2015年7月8日至今;由于2015年之前无0.25°×0.25°分辨率数据集,2015年之前的台风个例选用同样是来自全球数据同化系统(GDAS)的NCEP GFS-FNL(ds083.2)数据集(https://rda.ucar.edu/datasets/ds083.2/),其空间分辨率为1°×1°。为统一再分析资料空间分辨率,将该数据集采用双线性内插的方法插值到0.25°×0.25°网格上。
2.2 THWC指数的诊断应用本节首先采用NCEP再分析资料计算THWC指数并检验其在2018年第14号台风摩羯中的应用效果,然后选取2012—2018年所有影响海河流域的北上台风个例,采用空间相关分析、闭合中心极值对比的方法检验其普适性。
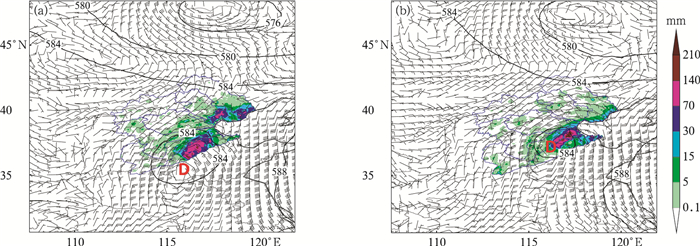
2.2.1 台风摩羯个例检验2018年14号台风摩羯于8月8日14时生成,并于12日23:35前后在浙江省温岭沿海登陆并继续北上,14日早晨开始影响海河流域。08时(图 2a)台风摩羯中心位于山东偏西部地区,500 hPa存在闭合等值线,环流比较完整,受其影响,北部高空槽系统位置偏北,850 hPa台风倒槽切变线向东北方向延伸至滦河及北三河的下游地区,流域内的大暴雨区(>70 mm)位于“摩羯”台风中心北侧的强辐合区以及倒槽切变线的最北端,且台风中心北侧强辐合区出现了140 mm以上的降水中心。14日14时,北侧高空槽系统基本稳定在流域的最北端,而台风摩羯继续北上,台风中心靠近徒骇马颊河的中游地区,暴雨区仍位于台风中心东北侧的强辐合区且位置略向北移至漳卫南运河下游地区。
|
图 2 2018年8月14日08时(a),14时(b)500 hPa高度场(黑线,单位:dagpm)、850 hPa风场以及滞后6 h后海河流域降水分布(填色) Fig. 2 The 500 hPa geopotential height (black lines, unit: dagpm), 850 hPa wind and distribution of rainfall (shaded area) in Haihe River Basin during following 6 h at (a) 08:00 BT and (b) 14:00 BT 14 August 2018 |
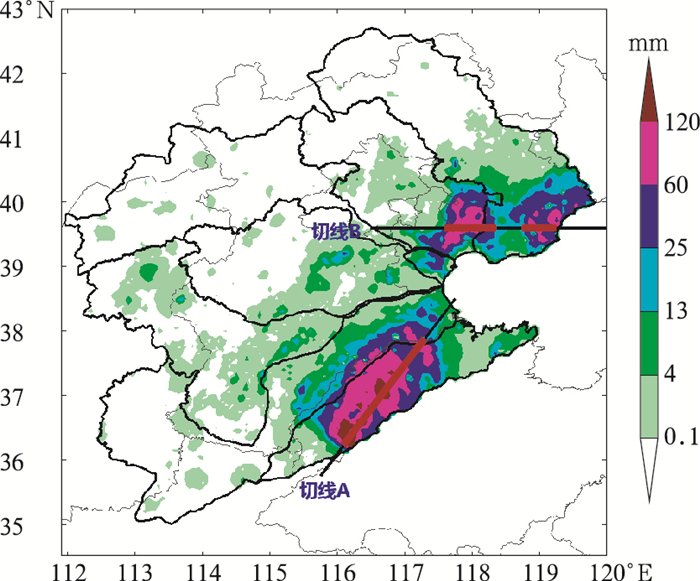
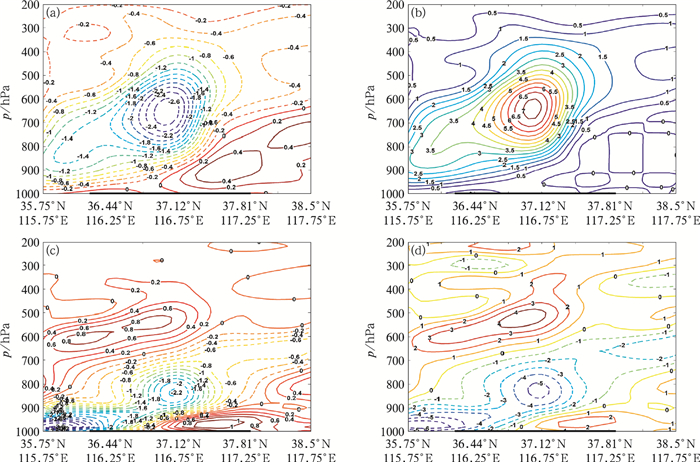
诊断分析14日08—14时台风中心偏北侧的暴雨区(图 3切线A)及切变线最北端暴雨区(图 3切线B)物理参数剖面,研究此次暴雨过程的机理。台风中心偏北侧的暴雨区物理参数剖面(切线A)如图 4所示,可以看到:暴雨区内部的垂直上升区域自西南向东北略向上抬升,在远离台风中心一端低层有明显的下沉气流侵入;尤其在大于70 mm的强降水区上空垂直上升运动剧烈且伸展到对流层顶部,垂直上升运动中心位于650 hPa附近(图 4a)。水汽凝结率(图 4b)分布与垂直速度剖面分布基本一致,均在强降水区上空650 hPa附近存在凝结中心,说明垂直速度对于水汽凝结率具有决定性作用。水汽通量散度(图 4c)呈现出低层强辐合、高空弱辐散的分布特征,其强降水区上空850 hPa附近存在强水汽辐合中心,说明水汽辐合集中在对流层中低层,对流层顶部由于水汽稀少而弱化了高层辐散特征。而θse通量散度(图 4d)在强降水区上空则表现出强度相当的低层辐合(中心位于850 hPa附近)、高层辐散(中心位于400 hPa附近)特征,这在一定程度上强调了高层辐散对低层辐合上升的维持加强作用以及带走积云对流释放潜热的通风作用,这样低层暖湿气流辐合、高层气流辐散的配置加大高低空的温湿差异,反映出强降水发生时的不稳定层结。综合而言,在强热力不稳定的环境下,对流层中低层(600 hPa以下)强水汽通量辐合增大了本地的水汽聚集,并垂直向上输送到对流层中层(800~500 hPa)时,在强垂直上升运动的作用下发生强烈的水汽凝结,最终形成此次台风暴雨。
|
图 3 2018年8月14日08—14时6 h降水量分布(填色)及剖面切线位置(黑实线) Fig. 3 Distribution of rainfall (shaded area) from 08:00 BT to 14:00 BT 14 August 2018 and the location of cross-section lines (black solid lines) |
|
图 4 2018年8月14日08时沿台风暴雨中心切线A剖面(x轴黑色加粗线为图 3中红色实线位置)的(a)垂直速度(单位:Pa·s-1), (b)水汽凝结率(单位:10-10g·s-1·cm-2·hPa-1), (c)水汽通量散度(单位:10-5 g·s-1·cm-2·hPa-1), (d)假相当位温通量散度(单位:10-2 K·s-1) Fig. 4 Vertical cross sections of line A (The bold black line is the red line in Fig. 3) (a) vertical veloctity (unit: Pa·s-1), (b) water condensation (unit: 10-10 g·s-1·cm-2·hPa-1), (c) divergence of moisture flux (unit: 10-5 g·s-1·cm-2·hPa-1), (d) divergence of pseudoequivalent potential temperature flux (unit: 10-2 K·s-1) at 08:00 BT 14 August 2018 |
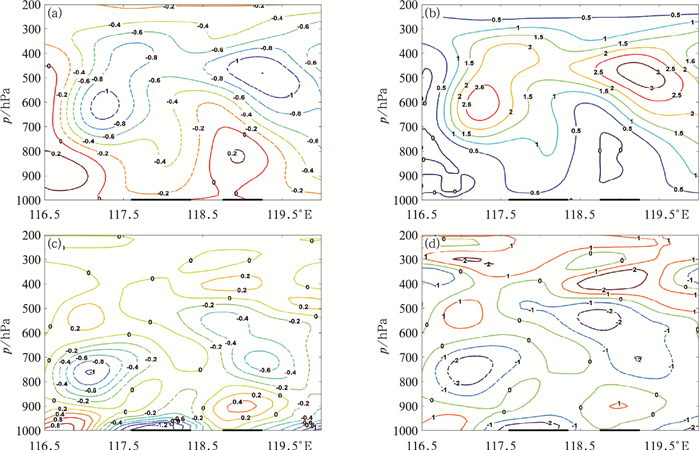
分析倒槽切变线顶端的暴雨区剖面(切线B)可以看到,位于118°E附近以及119°E附近两个暴雨中心上空的动力、水汽、不稳定条件远远小于台风中心附近暴雨区。118°E附近暴雨区除近地层950 hPa以下有较强的水汽通量辐合及θse通量辐合(图 5c、5d)外,其上空的各种物理参数均较弱但仍有明显的垂直上升运动及水汽凝结,为降水形成提供了一定动力、水汽条件;反而,在其西侧对流层中低层有明显的水汽强辐合中心(图 5c)且对应着中层的强垂直上升区及强水汽凝结区,因此随着系统东移,这可能是造成该地区强降水的一个主要原因。而119°E附近暴雨区低层800 hPa以下的动力条件较差,主要以下沉辐散气流为主(图 5a、5c);而水汽辐合区及上升凝结区位置偏高,水汽在750 hPa附近发生强烈辐合并上升至500 hPa附近发生强烈的水汽凝结(图 5a~5c),为降水发生提供了有利的动力、水汽条件;此外,与水汽通量辐合、水汽垂直上升凝结区对应的高度上,自下向上存在一对θse通量辐合、辐散区(图 5d),加大了上下层的温湿层结的差异,这为强降水发生提供了有利的热力不稳定层结。
|
图 5 同图 4,但为沿台风倒槽顶部暴雨中心切线B剖面 Fig. 5 Same as Fig. 4, but for vertical cross sections of the inverted trough rainstorm center line B |
引入基于动力、水汽、不稳定条件构建的新型强降水指数THWC对暴雨区进行诊断分析,THWC指数及各组成物理量分布特征如图 6所示。由图可见,组成THWC各物理量均在位于徒骇马颊河中上游的台风中心北侧暴雨区附近出现了大值区,但是热力不稳定参数θse通量散度差较暴雨区位置略有南偏,且大于40×10-6K·s-1·hPa-1的大值中心范围明显偏大(图 6a);表征动力不稳定参数的风暴相对螺旋度在徒骇马颊河中心位置较暴雨区更偏东偏北,强度明显偏大(达210 m2·s-2以上)(图 6b);整层最大水汽凝结率大值区与暴雨区基本一致但也略有南偏,其中心区与暴雨中心基本重合,但强度明显小于暴雨中心强度(仅为70×10-11 g·s-1·cm-2·hPa-1)(图 6c)。可见组成THWC指数的三个物理参数对于徒骇马颊河的暴雨区均有所反映,但是其范围或中心强度较暴雨区均有所偏差,而综合考虑了这三个因素的THWC指数大值区(图 6d)与台风中心北侧暴雨区几乎完全重合,尤其大于140×10-16 K·m2·kg-1中心位置及强度也与大于140 mm的暴雨中心基本重合,这说明新型强降水指数THWC对于暴雨区的位置及强度均具有较好的预报指示意义,其预报效果优于单一物理参数。
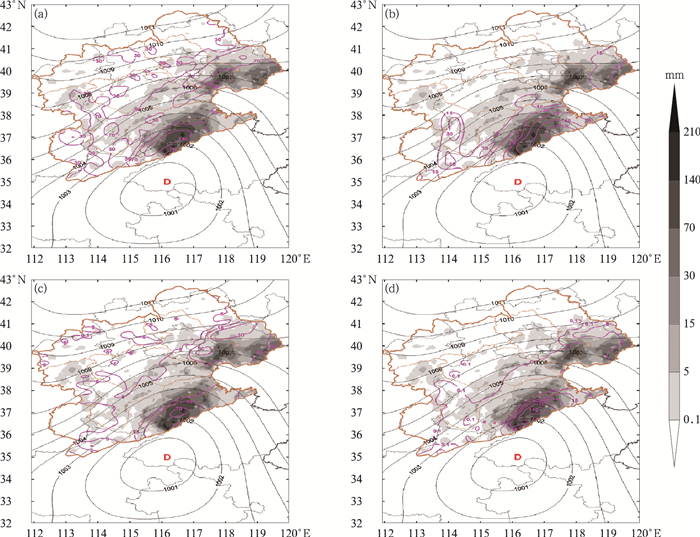
|
图 6 2018年8月14日08时海平面气压场(黑线, 单位:hPa)、物理量(粉线)与滞后6 h降水量分布(填色) (a)θse通量散度差(单位:10-6 K·s-1·hPa-1), (b)风暴相对螺旋度(单位:m2·s-2), (c)整层最大水汽凝结率(单位:10-11 g·s-1·cm-2·hPa-1), (d)THWC指数(单位:10-16 K·m2·kg-1) Fig. 6 Distributions of sea level pressure (black line, unit: hPa), physical parameters (pink line), and distribution of rainfall (shaded area) in Haihe River Basin during the following 6 h at 08:00 BT 14 August 2018 (a) θse flux divergence (unit: 10-6 K·s-1·hPa-1), (b) storm relative helicity (unit: m2·s-2), (c) the max water condensation (unit: 10-11 g·s-1·cm-2·hPa-1), (d) THWC index (unit: 10-16 K·m2·kg-1) |
但是值得注意的是对于滦河及北三河下游的台风倒槽顶部暴雨区,尽管组成THWC指数的物理量均有一定的反映,但其物理量中心区位置及强度与两个暴雨中心偏差较大,这说明对于具有明显的南风与东北风辐合、存在冷空气侵入破环台风环流的地区(图 2a),强降水THWC指数可能并不适用。进一步分析假相当位温及温度平流剖面可以看出,在台风中心北侧暴雨区中,低层存在很强的暖平流输送,从而减缓了北上台风衰减速度(杨晓霞等,2008;杜惠良等,2011),利于台风环流保持完整,暴雨发生在假相当位温锋区(等值线密集带)内(图 7a);而切变线顶部的降水区上空温度平流很弱,中低层有弱冷平流输送,没有明显的能量锋区(图 7b),这也从侧面印证了强降水THWC指数可能对于台风中心附近暴雨区的强降水诊断具有较好的适用性,而对于因被冷空气破坏后的台风环流造成的暴雨区适用性并不强。
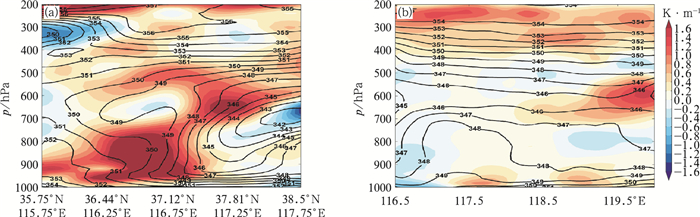
|
图 7 2018年8月14日08时假相当位温(实线, 单位:K)及温度平流(填色)剖面(a)沿台风北侧暴雨中心切线A剖面, (b)沿倒槽暴雨中心切线B剖面 (x轴黑色加粗线为图 3中红色实线位置) Fig. 7 Vertical cross sections of θse (solid line, unit: K) and temperature advection (shaded area) of (a) cross-section of typhoon main rainstorm area line A and (b) the inverted trough rainstorm line B in Fig. 3 at 08:00 BT 14 August 2018 (The bold black line in Fig. 7a is the red line in Fig. 3) |
北上台风作为影响我国北方沿海地区的重要天气系统,20世纪末期以来有明显增多的趋势(高松影等,2017;史得道等,2014)。本文通过统计2012—2018年台风个例发现,共有5个台风或减弱台风环流北上(1810号“安比”、1814号“摩羯”、1818号“温比亚”、1710号“海棠”、1210号“达维”)造成海河流域出现暴雨天气。为检验强降水指数THWC在北上台风暴雨中的普适性,本节通过分析THWC指数与降水落区分布的空间相关性以及两者闭合中心最大值差异来判别THWC指数对台风暴雨落区、强度的预报指示作用。
表 1依次分析了5个台风主要影响流域时段内THWC指数及各组成物理量与滞后6 h降水分布的空间相关性,可以看出强降水指数THWC及组成THWC指数的动力、水汽、不稳定参数均与滞后6 h的降水分布具有显著的空间正相关性(通过0.05的显著性水平检验)。对比三个组分,可以看出整层最大水汽凝结率与降水分布空间相关性最大,大多数时间段内空间相关系数可达0.7以上(通过0.05的显著性水平检验),尤其对于2018年最强北上台风1810号安比(台风北上直接穿过海河流域东部)而言,影响海河流域期间两者的相关系数均大于0.7,这说明水汽凝结率作为引起降水的物质基础,对未来6 h降水空间分布具有决定性作用。强降水指数THWC与降水分布的空间相关性似乎略小于水汽最大凝结率与降水的空间相关性,但是在大多数时段也基本上达到0.6以上(通过0.05的显著性水平检验),其结果仍优于θse通量散度之差、风暴相对螺旋度H与降水的空间相关性;尤其对于1814号“摩羯”8月14日14时和1210号“达维”8月3日14时,THWC指数与降水的空间相关性大于组成THWC指数的各组物理量与降水的空间相关性,预报效果优于单一物理参数。因此综合而言,强降水指数THWC对未来6 h降水落区预报具有较好的指示意义。
|
|
表 1 强降水指数THWC(ZTHWC)及其各组分与滞后6 h降水分布空间相关系数 Table 1 The spatial correlation coefficients between heavy rain THWC index (ZTHWC) and its component and precipitation in the following 6 h |
但值得注意的是THWC指数与少数台风暴雨区分布空间相关性相对较小,其中1813号“温比亚”8月19日08时、14时以及1710号“海棠”8月2日14时和20时,THWC指数与降水分布虽然具有一定的显著正相关性,但空间相关系数很小,仅在0.3左右(表 1)。分析原因这些时段台风中心位置离流域相对较远,流域内的暴雨或由台风外围的南风与东北风形成的倒槽切变线造成或为台风倒槽与北部高空槽系统相互作用造成(图略),暴雨区并不是由台风环流直接造成,这与1814号“摩羯”个例分析结果一致,再次从侧面证实了THWC指数仅对于台风中心附近的暴雨区预报具有较好的指示作用,对于由于有明显冷空气侵入台风环流而形成的倒槽切变线强降水或台风残余环流与高空槽系统结合造成的强降水预报效果并不理想。此外,对于1710号“海棠”8月3日02时,台风环流完全被破坏,强降水位于高空槽前低层850 hPa暖式切变线附近(图略),此时THWC三个组成物理量与降水分布空间相关系数尽管达到0.7以上,但THWC指数与降水的空间相关系数仅有0.59,这也从反面再次证明了THWC指数仅适用于台风中心附近环流较完整区域的暴雨预报。
文中对比THWC闭合中心值与滞后6 h强降水区中心最大降水值,探究THWC指数对台风暴雨区强度的预报指示作用(表 2),可以发现,对于1814号“摩羯”两个主要强降水时段,其THWC闭合中心值与暴雨中心最大降水量相当接近,很好地指示出此次降水过程各时段大暴雨、特大暴雨降水量级大小;但是综合分析这5个台风可以发现,THWC指数表现出非稳定性的特征,中心数值有时极端偏大(如1710号台风海棠8月3日02时THWC指数为1 142.6×10-16 K·m2·kg-1), 有时极端偏小(如1210号台风达维8月3日14时THWC指数为11.6×10-16 K·m2·kg-1);尤其1810号最强台风安比,2018年07月24日02时THWC闭合中心值为71.5×10-16 K·m2·kg-1,约为滞后6 h降水中心(137 mm)的1/2,而后一个时刻(08时)THWC闭合中心值为695.6×10-16 K·m2·kg-1)又为降水中心(127.7 mm)5倍多。基于此原因,文中继续将THWC指数进行改造,尝试消除单位的影响,构建了标准化的强降水指数ZTHWC,公式如下:
|
|
表 2 强降水指数THWC(ZTHWC)闭合中心最大值及滞后6 h降水中心值 Table 2 The max value of closed center in THWC index (ZTHWC) and precipitation centre in the following 6 h |
| $ \begin{array}{c} ZTHWC = \kappa \cdot \frac{{THWC - \overline {THWC} }}{{\sigma (THWC)}} = \\ \kappa \cdot \frac{{THWC - \frac{1}{n}\sum\limits_{i = 1}^n {THW{C_i}} }}{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{(THW{C_i} - \frac{1}{n}\sum\limits_{i = 1}^n {THW{C_i}} )}^2}} } }} \end{array} $ | (14) |
式中:κ=2称为平衡系数;i=1,2,…,n为流域内的网格点。
分析标准化的强降水指数ZTHWC可以发现,对于1814号台风摩羯暴雨,ZTHWC分布与滞后6 h的降水落区分布基本重合(图 8),相关系数在0.7上下(表 1),可以较好地预报出本次过程的降水落区分布;进一步分析这5个北上台风,ZTHWC指数与ZHC指数的空间分布十分相似,ZTHWC与滞后6 h降水落区的空间相关系数较THWC几乎未发生改变,因此对降水落区仍具有较好的预报效果(表 1)。而分析ZTHWC指数闭合中心最大值可以发现,标准化的ZTHWC指数相对稳定,没有出现极端值,虽然对于个别时刻ZTHWC会出现偏大或偏小的情况,但是对于大多数时刻来说ZTHWC指数明显优于THWC指数,普适性更强,基本能指示出未来6 h的最大降水量级大小,尤其对于具有完整台风环流的1810号“安比”两个强降水时段,ZTHWC中心值与降水中心最大值相差仅为十几,对本次过程暴雨中心量级定量预报效果非常好,这说明台风环流越完整,ZTHWC对台风暴雨区中心量级预报效果越好。
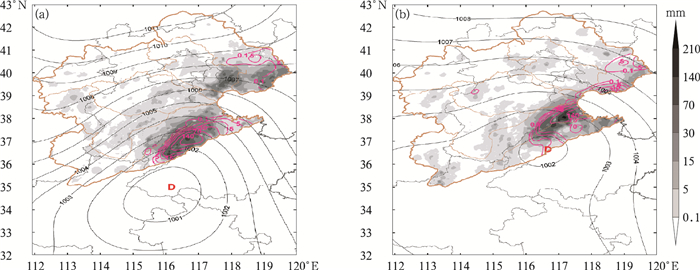
|
图 8 2018年8月14日08时(a)和14时(b)海平面气压场(黑线,单位:hPa)、ZTHWC指数(粉线)与滞后6 h降水量分布(填色) Fig. 8 Distributions of sea level pressure (black line, unit: hPa), ZTHWC index parameters (pink line) and rainfall (shaded area) in Haihe River Basin during the following 6 h at 08:00 BT (a) and 14:00 BT (b) 14 August 2018 |
基于降水发生的动力、水汽、不稳定三要素,采用“配料法”构建综合强降水指数THWC,并运用THWC指数对2018年8月13—14日北上影响海河流域的台风摩羯进行了诊断分析;最后选取2012—2018年影响海河流域的5个北上台风,通过分析THWC指数与降水实况分布的空间相关性、闭合中心最大值差异检验THWC指数对台风暴雨落区、中心量级预报的普适性,得到以下几点结论。
(1) 水汽凝结率包含了湿空气垂直运动条件、水汽条件以及潜热能量交换信息,对于需要潜热释放维持环流的台风系统来说较为重要。而基于动力、水汽、不稳定三者“交集”构建的强降水指数THWC全面描述了台风暴雨发生前期的强信号,THWC指数中引入的最大水汽凝结率能侧重反映出台风发展特点,从理论上讲更适合描述台风暴雨的发生。
(2) 组成THWC指数的三个物理量中,最大水汽凝结率作为降水产生物质基础,对未来6 h的由北上台风造成海河流域产生降水的落区分布具有一定的决定作用;而THWC指数预报效果在一定程度上优于单一信号,其大值区与未来6 h降水落区具有显著的正相关性,对未来6 h环流完整的台风暴雨落区分布具有很好的预报指示作用,但对于有冷空气侵入的台风倒槽及残余台风环流造成的暴雨,预报性不强。
(3) THWC指数可以指示台风暴雨区中心量级大小,尤其可以定量预报台风摩羯未来6 h台风暴雨中心大小,但是对于其他个例普适性不强,其暴雨中心量级的定量预报稳定性差,易出现极端值;而标准化的ZTHWC指数较THWC指数稳定,在大多数情况下,对未来6 h的台风暴雨分布及中心量级大小均有较好的预报意义,且台风环流越完整,预报效果越好,因此ZTHWC指数可以作为北上台风暴雨落区及中心量级定量预报指标。
曹楚, 王忠东, 刘峰, 等, 2016. 2013年"菲特"台风暴雨成因及湿位涡诊断分析[J]. 气象与环境科学, 39(4): 86-92. Cao C, Wang Z D, Liu F, et al, 2016. Diagnostic analysis of moist potential vorticity for heavy rain caused by "Fitow" (2013) typhoon[J]. Meteor Environ Sci, 39(4): 86-92 (in Chinese).
|
陈联寿, 孟智勇, 丛春华, 2017. 台风暴雨落区研究综述[J]. 海洋气象学报, 37(4): 1-7. Chen L S, Meng Z Y, Cong C H, 2017. An overview on the research of typhoon rainfall distribution[J]. J Mar Meteor, 37(4): 1-7 (in Chinese).
|
陈联寿, 许映龙, 2017. 中国台风特大暴雨综述[J]. 气象与环境科学, 40(1): 3-10. Chen L S, Xu Y L, 2017. Review of typhoon very heavy rainfall in China[J]. Meteor Environ Sci, 40(1): 3-10 (in Chinese).
|
程正泉, 陈联寿, 徐祥德, 等, 2005. 近10年中国台风暴雨研究进展[J]. 气象, 31(12): 3-9. Cheng Z Q, Chen L S, Xu X D, et al, 2005. Research progress on typhoon heavy rainfall in China for last ten years[J]. Meteor Mon, 31(12): 3-9 (in Chinese).
|
丁治英, 陈久康, 1995. 不同雨强台风的诊断对比与数值试验研究[J]. 南京气象学院学报, 18(2): 234-241. Ding Z Y, Chen J K, 1995. Diagnosis, comparative analysis and simulation of typhoons with different rainfall intensities[J]. J Nanjing Inst Meteor, 18(2): 234-241 (in Chinese).
|
杜惠良, 黄新晴, 冯晓伟, 等, 2011. 弱冷空气与台风残留低压相互作用对一次大暴雨过程的影响[J]. 气象, 37(7): 847-856. Du H L, Huang X Q, Feng X W, et al, 2011. The effect of the interaction between weak cold flow and typhoon depression on a rainstorm[J]. Meteor Mon, 37(7): 847-856 (in Chinese).
|
傅灵艳, 寿绍文, 黄亿, 等, 2009. 圣帕台风暴雨的非地转湿Q矢量的诊断分析[J]. 气象科学, 29(6): 727-733. Fu L Y, Shou S W, Huang Y, et al, 2009. Analysis on ageostrophic wet Q vector of the rainstorm caused by Typhoon "Sepat"[J]. Sci Meteor Sin, 29(6): 727-733 (in Chinese). DOI:10.3969/j.issn.1009-0827.2009.06.003
|
高留喜, 丛春华, 李本亮, 2008. 非地转湿Q矢量在北上台风"桃芝"造成山东大暴雨中的应用[J]. 热带气象学报, 24(5): 533-538. Gao L X, Cong C H, Li B L, 2008. Application of ageostrophic wet Q-vector in torrential rainfall of Typhoon "Toraji" in Shandong Province[J]. J Trop Meteor, 24(5): 533-538 (in Chinese). DOI:10.3969/j.issn.1004-4965.2008.05.014
|
高松影, 赵婷婷, 宋丽丽, 等, 2017. 1949-2015年北上热带气旋特征[J]. 气象科技, 45(2): 313-323. Gao S Y, Zhao T T, Song L L, et al, 2017. Study of northward moving tropical cyclones in 1949-2015[J]. Meteor Sci Technol, 45(2): 313-323 (in Chinese).
|
韩沁哲, 蔡荣辉, 匡方毅, 2009. 基于"配料法"的湖南省暴雨落区预报[J]. 广东气象, 31(1): 12-14, 18. Han Q Z, Cai R H, Kuang F Y, 2009. The ingredients-based methodology for forecasting rainstorm area in Hunan Province[J]. Guangdong Meteor, 31(1): 12-14, 18 (in Chinese). DOI:10.3969/j.issn.1007-6190.2009.01.004
|
何丽华, 孔凡超, 李江波, 等, 2007. 影响河北两次相似路径台风的湿位涡对比分析[J]. 气象, 33(4): 65-70. He L H, Kong F C, Li J B, et al, 2007. Analysis of wet potential vorticity of two similar typhoons affecting Hebei Province[J]. Meteor Mon, 33(4): 65-70 (in Chinese).
|
何钰, 陈小华, 杨素雨, 等, 2018. 基于"配料法"的云南短时强降水预报概念模型建立[J]. 气象, 44(12): 1542-1554. He Y, Chen X H, Yang S Y, et al, 2018. Forecast conceptual model establishment of short-time severe rainfall on Yunnan based on the "Ingredients"[J]. Meteor Mon, 44(12): 1542-1554 (in Chinese).
|
来小芳, 张艳玲, 陆汉城, 等, 2007. "配料法"用于长江下游暴雨预报[J]. 南京气象学院学报, 30(4): 556-560. Lai X F, Zhang Y L, Lu H C, et al, 2007. An ingredients-based methodology for forecasting rainstorm in the lower reaches of the Yangtze River[J]. J Nanjing Inst Meteor, 30(4): 556-560 (in Chinese). DOI:10.3969/j.issn.1674-7097.2007.04.018
|
李德帅, 王式功, 王金艳, 等, 2016. 一种新的综合物理指数构建及其在强降水预报中的应用[J]. 地球物理学报, 59(6): 1957-1970. Li D S, Wang S G, Wang J Y, et al, 2016. Construction of a new index and its application to forecasting heavy rainfall[J]. Chinese J Geophys, 59(6): 1957-1970 (in Chinese).
|
刘国忠, 黄开刚, 罗建英, 等, 2013. 基于概念模型及配料法的持续性暴雨短期预报技术探究[J]. 气象, 39(1): 20-27. Liu G Z, Huang K G, Luo J Y, et al, 2013. Research on the short-term forecasting technique of persistent rainstorm with conceptual model and ingredients based method[J]. Meteor Mon, 39(1): 20-27 (in Chinese).
|
刘勇, 郭大梅, 姚静, 等, 2015. 配料法在暴雨精细化预报中的应用[J]. 干旱气象, 33(3): 514-520. Liu Y, Guo D M, Yao J, et al, 2015. Applications of ingredients-based forecasting methodology to refine rainstorm forecast[J]. J Arid Meteor, 33(3): 514-520 (in Chinese).
|
史得道, 易笑园, 刘彬贤, 2014. 台风"达维"不对称结构特征分析[J]. 气象与环境学报, 30(3): 10-17. Shi D D, Yi X Y, Liu B X, 2014. Analysis of the asymmetric structure of Typhoon Damrey[J]. J Meteor Environ, 30(3): 10-17 (in Chinese). DOI:10.3969/j.issn.1673-503X.2014.03.002
|
孙继松, 陶祖钰, 2012. 强对流天气分析与预报中的若干基本问题[J]. 气象, 38(2): 164-173. Sun J S, Tao Z Y, 2012. Some essential issues connected with severe convective weather analysis and forecast[J]. Meteor Mon, 38(2): 164-173 (in Chinese).
|
孙建华, 赵思雄, 2000. 登陆台风引发的暴雨过程之诊断研究[J]. 大气科学, 24(2): 223-237. Sun J H, Zhao S X, 2000. Diagnoses and simulations of typhoon (Tim) landing and producing heavy rainfall in China[J]. Chin J Atmos Sci, 24(2): 223-237 (in Chinese). DOI:10.3878/j.issn.1006-9895.2000.02.11
|
孙力, 董伟, 药明, 等, 2015. 1215号"布拉万"台风暴雨及降水非对称性分布的成因分析[J]. 气象学报, 73(1): 36-49. Sun L, Dong W, Yao M, et al, 2015. A diagnostic analysis of the causes of the torrential rain and precipitation asymmetric distribution of Typhoon Bolaven (2012)[J]. Acta Meteor Sin, 73(1): 36-49 (in Chinese). DOI:10.3969/j.issn.1005-0582.2015.01.008
|
陶祖钰, 田佰军, 黄伟, 1994. 9216号台风登陆后的不对称结构和暴雨[J]. 热带气象学报, 10(1): 69-77. Tao Z Y, Tian B J, Huang W, 1994. Asymmetry structure and torrential rain of landing Typhoon 9216[J]. J Trop Meteor, 10(1): 69-77 (in Chinese).
|
吴星霖, 张云瑾, 郭荣芬, 等, 2008. 湿Q矢量分析法在台风"圣帕"暴雨过程中的应用[J]. 云南大学学报(自然科学版), 30(S2): 311-317. Wu X L, Zhang Y J, Guo R F, et al, 2008. Application of ageostrophic wet Q-vector analysis in torrential rain of typhoon "Sepat"[J]. J Yunnan Univ, 30(S2): 311-317 (in Chinese).
|
杨晓霞, 陈联寿, 刘诗军, 等, 2008. 山东省远距离热带气旋暴雨研究[J]. 气象学报, 66(2): 236-250. Yang X X, Chen L S, Liu S J, et al, 2008. A study of the far distance tropical cyclone torrential rainfalls in Shandong Province[J]. Acta Meteor Sin, 66(2): 236-250 (in Chinese). DOI:10.3321/j.issn:0577-6619.2008.02.010
|
姚秀萍, 于玉斌, 2000. 非地转湿Q矢量及其在华北特大台风暴雨中的应用[J]. 气象学报, 58(4): 436-446. Yao X P, Yu Y B, 2000. Non-geostrophic wet Q-vector analysis and its application to typhoon torrential rain[J]. Acta Meteor Sin, 58(4): 436-446 (in Chinese). DOI:10.3321/j.issn:0577-6619.2000.04.006
|
于玉斌, 姚秀萍, 2000. 对华北一次特大台风暴雨过程的位涡诊断分析[J]. 高原气象, 19(1): 111-120. Yu Y B, Yao X P, 2000. The diagnosis analysis of potential vorticity for a severe typhoon rainstorm in North China[J]. Plateau Meteor, 19(1): 111-120 (in Chinese). DOI:10.3321/j.issn:1000-0534.2000.01.014
|
余贞寿, 闵锦忠, 楼丽银, 等, 2010. 台风"凤凰"和"诺瑞丝"路径与降水分布对比分析[J]. 气象科技, 38(1): 32-36. Yu Z S, Min J Z, Lou L Y, et al, 2010. Analysis of typhoons "Fung-Wong" and "Norris" with similar tracks and different rainfall patterns[J]. Meteor Sci Technol, 38(1): 32-36 (in Chinese). DOI:10.3969/j.issn.1671-6345.2010.01.006
|
岳彩军, 2014. Q矢量、螺旋度、位涡及位涡反演在台风暴雨研究中的应用进展[J]. 暴雨灾害, 33(3): 193-201. Yue C J, 2014. Progress in application study of Q vector, helicity, potential vorticity and its inversion to torrential rainfall associated with typhoon[J]. Torr Rain Dis, 33(3): 193-201 (in Chinese). DOI:10.3969/j.issn.1004-9045.2014.03.001
|
张建海, 庞盛荣, 2011. "莫兰蒂"台风(1010)暴雨成因分析[J]. 暴雨灾害, 30(4): 305-312. Zhang J H, Pang S R, 2011. Analysis on the cause of rainstorm of the Typhoon Meranti (1010)[J]. Torr Rain Dis, 30(4): 305-312 (in Chinese). DOI:10.3969/j.issn.1004-9045.2011.04.003
|
张萍萍, 龙利民, 张宁, 等, 2012. "分型配料法"在湖北省暴雨预报中的应用研究[J]. 热带气象学报, 28(5): 771-776. Zhang P P, Long L M, Zhang N, et al, 2012. Applications of typing ingre-dients-based methodology to heavy rainfall forecast in Hubei Province[J]. J Trop Meteor, 28(5): 771-776 (in Chinese).
|
张亚洲, 梅华, 邓文彬, 等, 2011. 台风登陆后非对称降水的非地转湿Q矢量研究[J]. 气象科学, 31(6): 710-717. Zhang Y Z, Mei H, Deng W B, et al, 2011. Ageostrophic wet Q-vector study on asymmetric precipitation after typhoon landing[J]. J Meteor Sci, 31(6): 710-717 (in Chinese). DOI:10.3969/j.issn.1009-0827.2011.06.006
|
赵宇, 杨晓霞, 孙兴池, 2004. 影响山东的台风暴雨天气的湿位涡诊断分析[J]. 气象, 30(4): 15-20. Zhao Y, Yang X X, Sun X C, 2004. A diagnostic analysis of moist potential vorticity for typhoon heavy rain in Shandong Province[J]. Meteor Mon, 30(4): 15-20 (in Chinese).
|
周福, 钱燕珍, 朱宪春, 等, 2014. "菲特"减弱时浙江大暴雨过程成因分析[J]. 气象, 40(8): 930-939. Zhou F, Qian Y Z, Zhu X C, et al, 2014. Cause analysis on the severe rainfall in Zhejiang during the weakening of Fitow[J]. Meteor Mon, 40(8): 930-939 (in Chinese).
|
朱乾根, 林锦瑞, 寿绍文, 等, 2007. 天气学原理和方法:第4版[M]. 北京: 气象出版社: 1-642. Zhu Q G, Lin J R, Shou S W, et al, 2007. The Principles and Methods of Meteorology: 4th ed[M].
Beijing: China Meteorological Press: 1-642 (in Chinese).
|
Chien H H, Smith P J, 1977. Synoptic and kinetic energy analyses of Hurricane Camille (1969) during transit across the southeastern United States[J]. Mon Wea Rev, 105(1): 67-77. DOI:10.1175/1520-0493(1977)105<0067:SAKEAO>2.0.CO;2
|
Doswell Ⅲ C A, 1987. The distinction between large-scale and mesoscale contribution to severe convection:a case study example[J]. Wea Forecasting, 2(1): 3-16.
|
Doswell Ⅲ C A, Brooks H E, Maddox R A, 1996. Flash flood forecasting:an ingredients-based methodology[J]. Wea Forecasting, 11(4): 560-581. DOI:10.1175/1520-0434(1996)011<0560:FFFAIB>2.0.CO;2
|
Hoskins B J, McIntyre M E, Robertson A W, 1985. On the use and significance of isentropic potential vorticity maps[J]. Quart J Roy Meteor Soc, 111(470): 877-946. DOI:10.1002/qj.49711147002
|
Kunz M, 2007. The skill of convective parameters and indices to predict isolated and severe thunderstorms[J]. Nat Hazards Earth Syst Sci, 7(2): 327-342. DOI:10.5194/nhess-7-327-2007
|
McNulty R P, 1978. On upper tropospheric kinematics and severe weather occurrence[J]. Mon Wea Rev, 106(5): 662-672. DOI:10.1175/1520-0493(1978)106<0662:OUTKAS>2.0.CO;2
|
Schultz D M, Cortinas Jr J V, Doswell Ⅲ C A, 2002. Comments on "an operational ingredients-based methodology for forecasting midlatitude winter season precipitation"[J]. Wea Forecasting, 17(1): 160-167.
|
Wetzel S W, Martin J E, 2001. An operational ingredients-based methodology for forecasting midlatitude winter season precipitation[J]. Wea Forecasting, 16(1): 156-167. DOI:10.1175/1520-0434(2001)016<0156:AOIBMF>2.0.CO;2
|
Yao X P, Yu Y B, Shou S W, 2004. Diagnostic analyses and application of the moist ageostrophic vector Q[J]. Adv Atmos Sci, 21(1): 96-102. DOI:10.1007/BF02915683
|
 2020, Vol. 46
2020, Vol. 46 
