引言

强对流天气时空尺度小、发展快、致灾性强，准确预报其落区和强度可最大限度减少生命财产损失。传统的强对流天气预报是根据对流发展的环境条件，使用全球或者区域数值模式预报的对流参数来预报(薛纪善，2006)，无法提供强对流天气的精确信息(对流形态、对流移动速度、对流强度等)。随着计算能力的提高，对流许可尺度数值模式CPMs(convection-permitting models，通常认为水平格距小于5 km)已成为强对流天气预报中不可或缺的工具，如美国、法国、英国、日本等气象局目前使用的区域中尺度模式空间分辨率达到了1~4 km，可以直接预报γ中尺度对流风暴。CPMs在中尺度对流系统的回波形态、对流组织性、发生频率等方面明显优于采用对流参数化方案的低分辨率(格距10~20 km)数值模式(Weisman et al, 2008；陈德辉和沈学顺，2006)，能够为预报员提供直接的对流尺度产品(如雷达反射率因子、10 m瞬时大风等)，还可计算闪电、雷暴、冰雹等对流的强度和特征(McCaul et al, 2009)，为预报员判断强对流天气的类型和强度提供了更为直接的指导产品。

GRAPES_3 km模式作为我国自主研发的对流许可尺度中尺度数值模式，许晨璐等(2017)评估了该模式的降水预报，指出模式夏季日降水频率随降水量的变化与观测相似程度高，大降水频率和区域分布和实况较为吻合，并能够反映降水过程的日变化特征。唐文苑等(2018)利用分数技巧评分(FSS)对比评估了该模式和华东中尺度模式的组合反射率预报在华北地区几次典型强对流天气过程中的预报能力，探讨了该模式在强对流天气中良好的预报性能，但尚未利用多种检验方法对其进行全面评估。因此，本文以GRAPES_3 km模式的对流风暴预报为评估对象，并同GRAPES_Meso模式的预报评估结果对比，分析不同分辨率中尺度模式在强对流天气中的预报能力，从而为基于该类模式预报产品进一步发展强对流天气的智能网格预报技术和产品提供参考依据。

1 观测资料和模式资料

评估所用的观测资料为全国雷达组合反射率数据，空间分辨率为0.01°，时间分辨率为6 min，区域范围为12.2°~54.2°N、70°~135°E。模式资料来源于GRAPES_3 km和GRAPES_Meso两个中尺度模式，两者差异主要体现在：(1)预报区域和空间分辨率不同(徐枝芳等，2013；黄丽萍等，2017)；(2)起报时间和预报时效不同；(3)模式初值和背景场不同(毛冬艳等，2014)。具体说明见表 1。

由于模式预报与实况观测数据时空分辨率不同，统一空间分辨率时将观测资料进行了稀疏化，但为保留对流天气的强回波信息，取所稀疏网格周边区域的最大值。

2 检验方法和检验对象 2.1 检验对象

以对流风暴作为检验对象来评估GRAPES_3 km模式对流天气的预报能力。对流风暴在雷达观测中定义为组合反射率超过一定阈值的具有一定体积的连续区域。本文评估时将其划分为三个等级(Dixon and Wiener, 1993)：对流风暴外围的层状云带、对流风暴及强对流风暴；其最低阈值分别定义为20、35和50 dBz。

首先使用点对点TS评分对两个模式的逐小时预报进行整体评估，检验区域为我国中东部地区(17°~50°N、102°~135°E)，检验时段为2018年4—8月。由于GRAPES_3 km模式为一日两次的预报，GRAPES_Meso模式为一日8次滚动预报，评估时采用两者相同的起报时间(每日08时和20时)进行对比评估。

应用新型检验方法进行评估时，为使结果更有代表性，选取了10次强对流天气过程(见表 2)，预报区域包含了华南、江汉江淮、华北黄淮等强对流较为多发的区域，检验时段为强对流个例发展较为强盛的时段。模式评估对象为：对流发生时，GRAPES_3 km模式前一日20时和当日08时起报的预报；GRAPES_Meso模式最临近(最新)起报和前一时次(次临近)起报的预报。通过两个模式不同起报时间的预报效果对比，评估对流许可尺度模式和快速更新同化模式在对流风暴预报中的性能。

2.2 检验方法 2.2.1 传统点对点检验

TS评分是基于二分类表，针对预报和观测发生和未发生有四种可能的情况计算模式与实况匹配的程度。传统点对点检验是对比预报格点和观测格点重合程度，给出总体评分。TS评分综合考虑了命中(a)、空报(b)和漏报(c)的情况，计算公式如下：

$ TS = \frac{a}{{a + b + c}} $

(1)

2.2.2 时空邻域TS检验

传统预报检验具有一定的参考意义，但是对于高分辨率模式，随着格点间距的减小，微小的位置和形态的差异在传统的评分会造成很大的影响(命中率和虚警率的双重惩罚)。邻域法解决了“双惩罚”现象(Ebert, 2008)，能够接受预报值和观测点位置上的细微差异。邻域法通常是指空间邻域法(Ghelli and Lalanrette, 2000)，是指将预报格点和以其为中心向外拓展的实况邻域进行的点对面评分。强对流天气发生发展迅速、局地性强，对流风暴在短时间内形态、强度均可能有比较大的变化，评估时使用预报整点的瞬时值和对应时刻的整点实况，可能无法客观评价对流在该时段内发展变化，因此需要引进时间邻域的概念，使用累积实况来体现该时间段强对流的影响区域和强度变化。

本文的邻域TS法同时引入时间邻域和空间邻域(简称为时空邻域TS法)，具体算法是：以0.0、0.4°、0.8°、1.2°、1.6°、2.0°、3.0°、4.0°方形网格为空间邻域，分别以雷达回波在Δt、2Δt、3Δt时段内超过某一阈值(如35 dBz)的次数为时间邻域，计算TS评分。邻域TS法是传统点对点TS方法的延伸，当邻域尺度为0时，与点对点评分一致。利用邻域尺度可变的特性，时空邻域TS法可以得到单点预报时(比如机场预报等)模式预报的最优技巧尺度，这个尺度是向用户显示预报结果的合适尺度。

2.2.3 分数技巧评分

分数技巧评分(FSS)是基于邻域法给出空间技巧评估的另一个手段，比较预报邻域与相应观测邻域的差异，是“面对面”的检验，衡量场的相似度(Roberts and Lean, 2008)。

$ FSS = 1 - \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{P_{{\rm{for }}}} - {P_{{\rm{ols }}}}} \right)}^2}} }}{{\frac{1}{n}\sum\limits_{i = 1}^n {P_{{\rm{for }}}^2} + \frac{1}{n}\sum\limits_{i = 1}^n {P_{{\rm{ole }}}^2} }} $

式中：P_fcst和P_obs分别表示邻域内预报格点数和观测格点数占邻域窗口的比例；n是窗口的个数，当FSS值趋向于1时预报技巧最高。

将“最低技巧尺度”定义为FSS值超过0.5+0.5f_obs的尺度，其中f_obs为研究区域内满足某一给定阈值的观测格点占整个区域的百分比。FSS能够评估模式对于不同尺度对流风暴预报的位置偏差，并给出相应的最低预报技巧尺度。

2.2.4 对象检验

对象检验(MODE)也是“面对面”的检验(Davis et al，2006)，通过识别和匹配不同空间场里的对象，计算对象的相似度并评估两个场的综合相似度(李佰平等，2016；茅懋等，2016; 刘凑华和牛若云，2013)。该方法除了能够评估空间场的相似程度外，还可以检验对象的位置、面积、轴向、形状等特征。其有5个步骤：(1)卷积滤波；(2)聚类：将离散的小对流风暴合并成大对流风暴(Marzban and Sandgathe, 2006)；(3)椭圆识别：对聚类后的对流风暴进行椭圆拟合(Rodrigue and Laio, 2014)；(4)匹配：根据面积膨胀法，取椭圆交集最大的配对；(5)评分：利用面积重叠比计算最后的评分值。

3 典型强对流个例检验

新型检验方法是否能够客观评估模式对流风暴的预报能力？以2018年3月19日的强对流过程为例进行探讨。该过程是一次较为典型的华南前汛期由地面锋面触发的强对流天气，锋面呈“人”字型分布。午后到傍晚，广西多站观测到冰雹、8级以上雷暴大风。

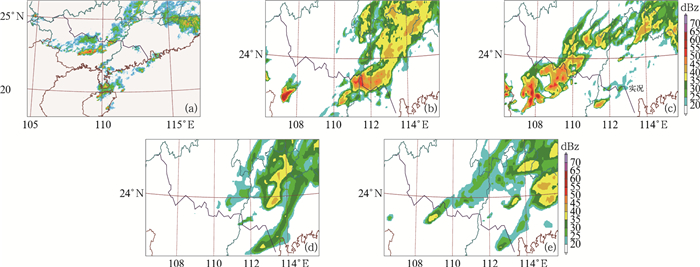
首先，检验MODE拟合的椭圆能否较为准确地代表对流风暴尺度、位置、轴角等基本特征，评估是否具有可信性？以19日18时实况为例(图 1)，从预报员的主观检验来看，GRAPES_3 km模式前一日20时起报的预报位置偏东，强度偏弱，当日08时起报的预报最好，能够较为准确地预报对流风暴及其外围层状云带，但是对强对流风暴的形态预报(南北向)与实况(东西向)有一定的差异。GRA- PES_Meso模式预报对流风暴的位置明显偏东、强度偏弱，对强对流风暴的预报基本漏报。

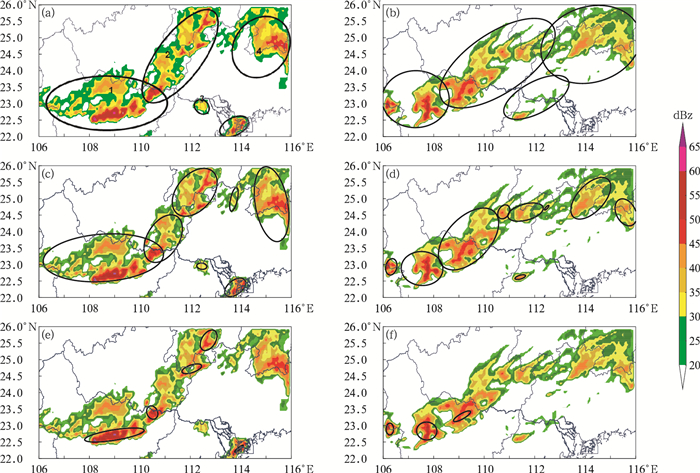
图 2为不同聚类尺度的MODE评分，可以评估模式对不同尺度对流风暴的预报能力(Tustison et al, 2001; Roberts and Lean, 2008)。GRAPES_3 km模式的MODE评分明显高于GRAPES _Meso模式，这也与预报员的主观判断一致。以GRAPES_3 km模式08时起报的最优评估尺度(分别为0.2°、0.6°、3.0°)拟合的椭圆空间分布(图 3)可见，MODE识别和匹配的椭圆基本能反映对流风暴的尺度、形状等特征，可以用其作为模式评估的依据。

FSS评估结论与MODE大致相同(图 4)，GRAPES_3 km模式的FSS评分显著高于GRA- PES_Meso模式。GRAPES_3 km模式当日08时起报的预报最好，各阈值均达到了最低技巧尺度(0.3°、0.8°、3.5°)，而前一日20时起报的空间偏差较大，尤其是强风暴预报没有达到最低技巧尺度。GRAPES_Meso模式对于35 dBz以上的对流风暴均没有达到最低技巧尺度。

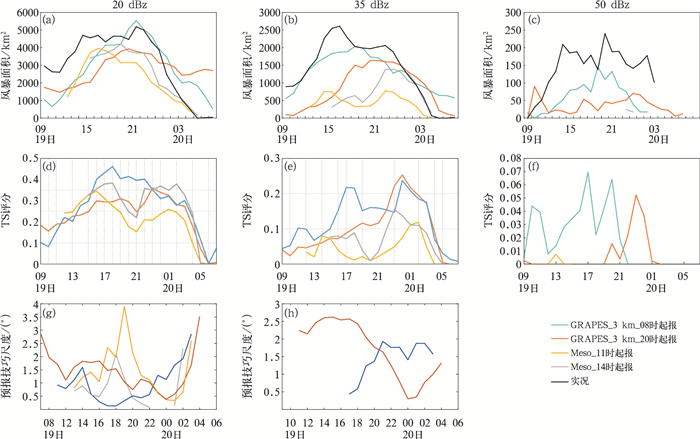
采用MODE拟合的风暴面积结合邻域TS评分和FSS的最低技巧尺度来分析对流风暴发展变化的预报能力。图 5a~5c中黑色实线为基于MODE最优技巧尺度拟合的对流风暴面积实况。19日午后对流风暴的面积快速增长，在15—16时和21—22时两个时段，面积达到峰值，呈现出双峰结构。GRAPES_3 km模式的对流风暴面积预报较为准确，但是对初生时间预报滞后，其中当日08时起报滞后2 h左右，对于午后到傍晚时段预报较好；前一日20时起报滞后4 h，对于傍晚到前半夜的预报与实况更接近。GRAPES_Meso模式是快速更新同化模式，对流初生和发展的时段预报和实况较为一致，能够看到明显的双峰结构，但由于空间分辨率较粗，对流风暴的面积预报明显偏小。

邻域TS评分和FSS可以评估模式对不同阶段的对流风暴发展变化的能力。对于08—21时时段，GRAPES_3 km模式当日08时起报的对流风暴(35 dBz)邻域TS评分高于其他预报，其中17时TS评分最高，FSS也显示该时刻最低技巧尺度最小(0.3°)，位置预报偏差最小。对于50 dBz的强对流风暴，评分具有明显的日变化特征，模式在热力条件更好的午后到前半夜的刻画能力明显好于其他时段，傍晚到前半夜评分最高，其他时次评分基本为0。但由于模式对强对流风暴的面积预报仅为实况面积的一半，所以邻域TS评分最高仅为0.07，FSS未达到最低技巧尺度。对于21—02时时段，FSS和邻域TS评分均显示GRAPES_3 km模式前一日20时起报的对流风暴预报最好，其中在00时时TS评分最高，35 dBz的邻域TS评分达到0.25，最低技巧尺度(空间偏差)为0.2°左右。该起报时间的强对流风暴面积预报为实况的1/5，漏报较多，因此邻域TS评分最大值仅为0.06，FSS也显示无预报技巧。GRAPES_Meso模式对流风暴预报的TS评分仅为GRAPES_3 km模式的一半，对强对流风暴无预报能力为0(图 5f)，FSS评估该模式预报未达到最低技巧尺度(图略)，这可能与对流风暴面积预报偏小有关。

从本次强对流过程来看，GRAPE S_3 km模式预报对流的初生时间滞后，对流风暴的位置和面积预报较好。GRAPES_Meso模式能够较为准确地描述对流初生和发展的时间，但是对对流风暴的强度、面积预报能力较差。预报员制作强对流天气预报时可以综合考虑两模式的特点对主观预报进行订正。

4 整体检验评估

从前文的典型个例来看，新型检验方法能够较为客观评估模式对流风暴的预报能力，因此下文中将针对2018年4—8月两个模式预报效果进行整体检验，以得到具有统计意义的评估结论。

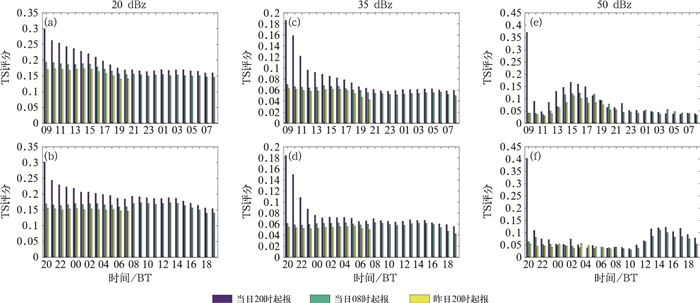
4.1 点对点TS评分整体评估

图 6是基于传统点对点TS方法对GRAPES_3 km模式对流风暴预报进行的整体评估。为分析不同起报时间的预报效果，将不同起报时间对同一时刻实况的预报评分放在一起对比。例如预报员在制作强对流天气预报时，在某一时刻(如09时)，对应有三个不同起报时间的预报, 即图中标注的当日08时、昨日20时和昨日08时起报的预报，哪个起报时间的预报效果最好？

从逐小时评分变化可以看到：(1)模式起报的最初3 h预报评分最高，基本不存在“spin-up”的问题，3 h后评分明显下降，这与初始场加入云分析有关。云分析是指加入观测和模式的初始分析构造初始云水物理场，缓解模式需要运行几个小时才能成云致雨的过程。云分析的有效时间大概在3 h左右，与之前的研究结论(Xiao and Sun, 2007)相吻合。(2)50 dBz以上的强对流风暴预报评分具有明显的日变化特征，午后到傍晚评分最高，凌晨评分最低。20和35 dBz日变化不显著。

从不同起报时间对于相同时间的预报对比可以看到：(1)起报时间越新预报效果越好，预报员可以直接采用最新预报产品；(2)评分发展变化的趋势并不一致，这间接反映了不同起报时间的预报对于对流风暴发展过程的刻画是有区别的；(3)50 dBz评分峰值与20、35 dBz峰值无明显对应关系。通过个例检验发现，50 dBz评分高的个例，对应的20、35 dBz的范围通常偏小。

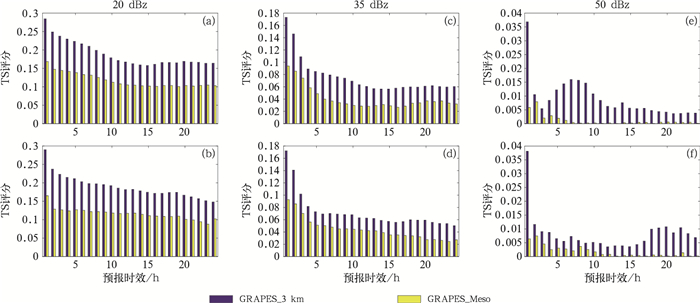
从GRAPES_3 km和GRAPES_Meso两个模式不同预报时效的对比来看(图 7)，无论是08时还是20时起报，GRAPES_3 km模式的预报效果均优于GRAPES_Meso模式。20和35 dBz的预报，GRAPES_3 km模式TS评分是GRAPES_Meso模式的两倍。大于50 dBz的预报评分差异更加明显，GRAPES_3 km模式在严格点对点检验中评分仍能达到0.01以上，说明该模式对于强对流风暴具有一定的预报能力。GRAPES_Meso模式的预报评分在多个时次几乎接近于零，说明该模式对于强对流风暴的预报能力非常有限，这与位置和强度预报偏差都有关系。

4.2 时空邻域TS方法评估

Lynn et al(2012)对空间分辨率为4 km的高分辨率模式预报进行检验评估时，由点对点检验改为空间邻域为12、36 km时，预报评分大大提高。但邻域的扩大降低了预报的空间分辨率，会使预报信息被平滑(Mass et al, 2002)。因此使用邻域法检验需要关注的问题是：模式对于哪个邻域尺度可预报性最强、预报技巧最高？模式最优预报技巧尺度(Roberts, 2005)是多少？

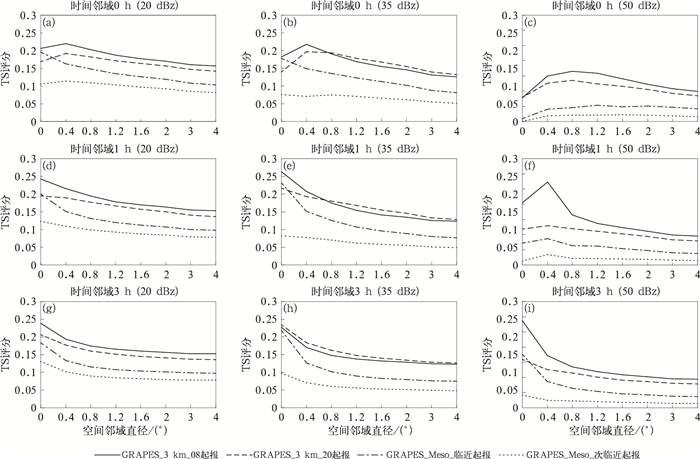
图 8是时空邻域TS评分，横坐标为空间邻域尺度(点对面直径)。从传统的点对点评分来看(第一行第一列当空间邻域为0时)，对于20和35 dBz，预报评分高低依次是：GRAPES_3 km模式当日08时起报、GRAPES_Meso模式最临近时刻起报、GRAPES_3 km模式前一日20起报、GRAPES_Meso模式前一个时刻起报的预报。考虑了空间邻域时(图 8a~8c)，GRAPES_3 km模式当日08时起报的预报仍为评分最高的预报，与点对点方法判定的结论一致。

空间邻域使TS评分有所提高，GRAPES_3 km模式在邻域尺度0.4°时TS评分达到最大，GRA- PES_Meso模式随邻域尺度增大TS评分持续下降，说明该模式由于实时同化最新资料的缘故，虽然对位置预报较好，但当忽略一定的空间偏差(邻域)时，模式对范围和形态的预报能力逊于GRAPES_3 km模式。再同时考虑时间邻域时(图 8d~8f、图 8g~8i)结果又有所不同。时间邻域尺度的增加扩大了实况样本的数量，当拓展到1 h(图 8d~8f)可以使模式预报的空间偏差完全忽略，且评分高于空间邻域的瞬时实况评分。当拓展到3 h(图 8g~8i)时由于实况样本过多导致漏报率增加，因此评分低于时间邻域为1 h的评分，这也说明中尺度系统对于局地影响的时间尺度在1 h左右。

对于尺度较小的50 dBz的强对流风暴预报，传统点对点TS评分(图 8c中空间邻域为0时)已经展示出GRAPES_3km模式的优越性，TS评分是GRAPES_Meso模式的4倍，这与4.1节结论一致。仅考虑空间邻域时，GRAPES_3 km模式邻域尺度在0.8°时，GRAPES_Meso模式在1.2°左右预报评分最高，说明GRAPES_3 km模式对强对流风暴预报的空间偏差更小。同时考虑时间邻域时，两个模式在时间邻域拓展到3 h评分最高，GRAPES_3 km模式采用空间点对点TS评分最高，GRAPES_Meso模式仍存在一定的空间偏差，邻域尺度为0.2°。

综合以上可以发现：(1)传统点对点方法和时空邻域TS方法检验结论是具有一致性，点对点方法对于高分辨率模式对流风暴预报的评估也具有参考价值。(2)时空邻域TS高于传统点对点TS评分。对于不同阈值的对流风暴，模式评估的时空邻域尺度不同：GRAPES_3 km模式对于20和35 dBz采用时间邻域为1 h，空间点对点时预报技巧最高；50 dBz采用时间邻域3 h，空间点对点时预报技巧最高。这与不同尺度对流风暴的可预报性一致，强对流风暴尺度小可预报性差，需要的时空邻域尺度也就更大。

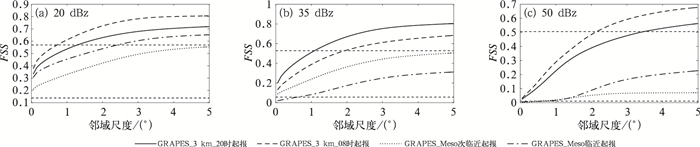
4.3 FSS评估

FSS通过邻域(窗区)大小的变化，评估预报和实况在邻域中的发生频率差异来分析模式的预报能力，当模式预报存在可容忍的空间偏差时仍能给出有价值的评分结果(Millermaier and Roberts, 2010)。图 9可见FSS评估与点对面的邻域法TS评估结论一致，GRAPES_3 km模式在各个邻域的FSS评分均高于GRAPES _ Meso模式，其中当日08时起报的预报技巧最高。

表 3为FSS评估的模式最低技巧尺度，该尺度是根据图 9中第二个横虚线对应的横坐标确定，尺度越小说明模式预报的空间偏差越小。GRAPES_3 km模式对于不同阈值的对流风暴均能达到最低技巧尺度，而GRAPES_Meso模式对于35 dBz以上的预报无法达到最低预报技巧尺度，对流风暴的预报能力较差。

4.4 MODE评估

使用MODE评估时，聚类尺度等参数很大程度依赖于研究者的主观判断(Davis et al，2006)。本节通过对比两个模式不同聚类尺度下的对流风暴预报与实况的差异，评估MODE方法的最优评估聚类尺度。

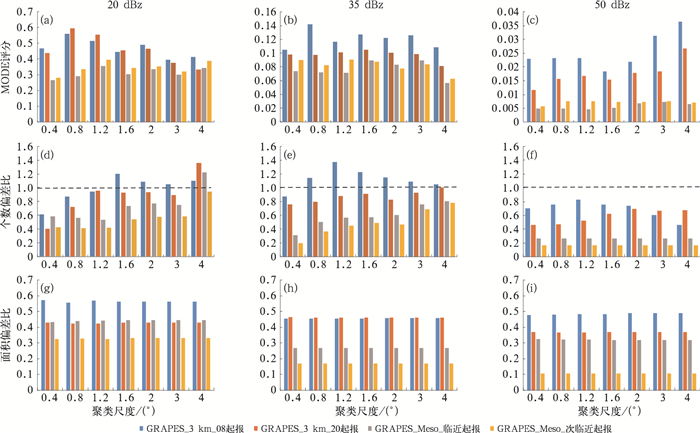
图 10a~10c为不同聚类尺度的MODE评分。GRAPES_3 km模式不同的聚类尺度MODE评分均高于GRAPES_Meso模式。20和35 dBz的评分呈中间高两边低的“拱形”，GRAPES_3 km模式最优评估聚类尺度为0.8°，GRAPES_Meso为1.2°，说明GRAPES_3 km模式能够刻画更小尺度对流风暴的特征。对于50 dBz的强对流风暴，MODE评分随着聚类尺度增大而提高，模式最优预报尺度为4°，该尺度说明两个模式强对流风暴特征的预报能力均比较有限。对比来看，GRAPES_3 km模式对于强对流风暴预报更好，当日08时起报的预报MODE评分是GRAPES_Meso模式的3倍。

表 4为模式基于MODE方法的最优预报技巧尺度。MODE的聚类尺度与FSS的邻域窗口相似，都是分析不同邻域中预报场和观测场的差异，但是MODE同时考虑了对流风暴的个数、面积、形状、轴向等信息，FSS仅考虑邻域发生概率，所以虽然两方法对模式预报优劣的评估结果一致，但最优空间邻域尺度的范围有所差异。50 dBz的强对流风暴预报MODE的最优尺度更大，说明模式相对于对流风暴的面积和强度，对于形状、轴向等特征的预报较差。

图 10d~10f为不同聚类尺度的椭圆个数偏差比(预报与实况的比值，等于1时最接近实况)。对于20和35 dBz，GRAPES_3 km模式08时预报偏差比接近于1，与实况个数较为一致，前一日20时起报的预报椭圆个数较实况略偏少；GRAPES_Meso模式预报较实况偏少明显，仅为实况个数的一半，这也是其TS评分较低的原因之一。对于50 dBz以上的强对流风暴，两个模式预报个数均偏少，GRAPES_3 km模式为实况的一半，GRAPES_Meso模式仅为实况的1/5。

图 10g~10i为不同聚类尺度的椭圆面积偏差比，两个模式对于各个尺度的对流风暴面积均低估，特别是强对流风暴预报面积明显偏小，这与Cai and Dumais(2015)在对流许可尺度模式的检验结果类似。对比来看，GRAPES_3 km模式面积预报明显好于GRAPES_Meso模式，其中当日08时起报的预报效果最好。

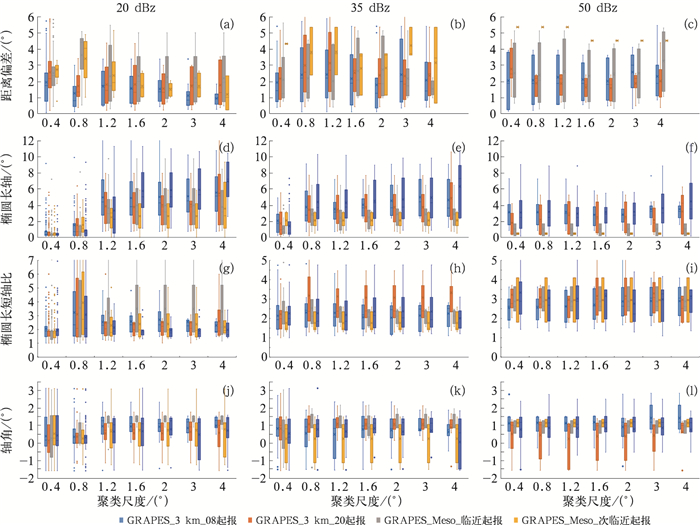
图 11以箱线图的形式统计不同聚类尺度椭圆的距离偏差、长轴、长短轴比和轴角, 分别体现了对流风暴的尺度，形状和角度。

距离偏差(图 11a~11c)是指MODE拟合的对流风暴中心的距离偏差，距离越小说明模式预报位置偏差越小。从距离偏差的中值和离散度来看，GRAPES_3 km模式预报对流风暴的距离偏差在1°~3°左右且离散度较小，GRAPES_Meso模式的距离偏差在3°~4°且离散度较大，说明GRAPES_3 km模式对位置的预报确定性更高、更稳定，同时距离偏差较小。

椭圆长轴(图 11d~11f)基本反映了对流风暴的尺度，总体来看，两个模式对小尺度的对流风暴(聚类尺度小于1.2°)预报尺度偏大、对于较大尺度的对流风暴(聚类尺度大于1.6°)预报尺度偏小。从不同模式不同起报时间的预报来看，GRAPES_3 km模式08时起报与实况较一致，对中小尺度(聚类尺度为0.8°~2.0°)对流风暴的尺度预报较好，前一日20时起报预报尺度偏小且离散度较大。GRAPES_Meso模式最临近时刻起报的对流风暴预报尺度明显偏小，仅是实况的一半，50 dBz的强对流风暴尺度预报为实况的1/6；而前一时刻起报的预报基本无预报能力。

椭圆长短轴比和轴角(图 11g~11i)反映了对流风暴的形态。长短轴比接近1是圆形，大于1时是椭圆型。轴角是椭圆与正东分量的夹角，夹角范围为，逆时针旋转为正，夹角为正时椭圆为西南—东北向，夹角为负则椭圆为东南—西北向，轴角越大说明越倾斜(南北方向分量越大)。两个模式对尺度较小的对流风暴形状预报更圆且轴角更小，尺度较大的对流风暴预报形状更扁轴角更大。GRAPES_3 km模式当日08时起报的形态预报与实况较为一致，前一日20时起报较实况更扁，轴角更偏向东南—西北向。GRAPES_Meso模式形态预报较实况更圆，轴角更小。GRAPES_Meso模式对流风暴形态预报的偏差较GRAPES_3 km模式更大，无法准确刻画出对流风暴的细节特征，这可能与其分辨率较低有关。

综合以上，基于MODE方法的对流风暴特征预报，GRAPES_3 km模式位置预报的偏差更小且确定性更高，能够较好地反映出β中尺度对流风暴的尺度和形态，但是对γ尺度对流风暴尺度预报偏大、形状偏圆、轴角偏小，对α尺度对流风暴尺度预报尺度偏小、形状偏扁、轴角偏大。GRAPES_Meso模式预报的位置偏差较大，各个尺度预报均偏小，形状预报较实况偏圆、轴角偏小，对50 dBz以上的强对流风暴预报能力较差。

5 结论与讨论

本文通过传统点对点TS评分，时空邻域TS、FSS和MODE对比分析了GRAPES_3 km和GRAPES_Meso两个模式对流风暴的预报能力，结论如下：

(1) 传统点对点TS评分显示，GRAPES_3 km模式对于不同阈值的对流风暴预报均优于GRA- PES_Meso模式，对于不同起报时间的预报，起报时间越新预报效果越好。GRAPES_3 km模式最初3 h评分最高，基本不存在“spin-up”，3 h后评分明显下降。50 dBz以上的强对流风暴预报具有明显的日变化特征，20和35 dBz日变化不显著。

(2) 邻域TS方法能够得到点对面预报时的最优评估尺度。两个模式对于20和35 dBz最优评估尺度为时间邻域尺度为1 h，空间采用点对点；对于50 dBz的强对流风暴时间邻域尺度需要拓展到3 h，此时GRAPES_Meso模式仍有0.4°的空间偏差(空间邻域直径)，说明GRAPES_Meso模式预报时间和空间差异均较大。当忽略一定的空间偏差(邻域)时，GRAPES_3 km模式预报TS评分明显高于GRAPES_Meso模式，其中GRAPES_3 km模式当日08时起报的预报效果最好。

(3) GRAPES_3 km模式在各个邻域的FSS均高于GRAPES_Meso模式，对于不同阈值的对流风暴GRAPES_3 km模式均能达到最低技巧尺度，GRAPES_Meso模式对于35 dBz以上的对流风暴预报无法达到最低预报技巧分数。

(4) MODE可以客观识别对流风暴的位置、形状、方向等信息，GRAPES_3 km模式对流风暴个数的预报较好，面积预报偏小，对β中尺度对流风暴的预报效果最好。GRAPES_Meso模式的对流风暴面积、个数、尺度预报均低估，无法准确刻画对流风暴细节特征。MODE评估的强对流风暴的最优尺度大于FSS，原因可能与模式对强对流风暴的形状、轴向等刻画能力较差有关。

(5) 通过强对流典型个例评估表明，多种评估方法可以客观全面地评估对流风暴特征的预报性能，分析模式对流风暴初生和发展变化的预报能力，从而给模式开发人员重要的反馈信息，同时为预报员在模式使用时做出修正和正确的决策方案提供依据。

本文通过几种不同检验方法对GRAPES_3 km模式和GRAPES_Meso模式进行了整体评估，每种评估方法虽然给出的信息不同，但结论基本一致，都可以作为高分辨率模式评估的依据。这几种检验方法的区别为：时空邻域TS是“点对面”的检验，这对于机场等固定点的单点预报非常有意义。FSS是将实况邻域和模式邻域的两个场进行比较，衡量不同尺度(邻域)发生概率的相似度，同时FSS可以给出模式的最低预报技巧尺度。MODE也是基于两个场的检验，但对检验对象是否配对的条件更加严格。MODE需要人为地规定卷积和聚类尺度，更适合针对小区域短时临近预报中的人机交互检验。综合以上，用户可以根据不同目的选择不同的检验方法，单一的检验方式不可能包含模式预报性能的全部信息。本文所得结果可为智能网格预报产品和业务短临预报提供参考。另外，发展检验技术的实时评估结果也可为多模式集成预报技术提供模式评估结果，今后将进一步研究这些评估方法在多模式集成预报技术中的应用方法。