引言

地球表面的60%~70%被云覆盖；云、降水物理过程是大气水循环的核心组成部分，是地球大气的热量、水分和动量平衡的关键因素，它不仅影响局地和短期天气过程，也影响着大气环流和全球气候变化。此外，云与大气辐射的相互作用还会影响大气辐射平衡、大气污染传输等。

数值模式中云计算方案的优劣很大程度上决定着模式的性能，因此云计算方案的研究越来越得到重视。关于云量计算方面，已有的工作主要有诊断方案、预报方案、统计方案和统计动力预报方案等。云量诊断方案的代表是Slingo(1987)的工作；云量预报方案中Tiedtke(1993)，通过对云形成与消散的影响因子研究，推导出了云量预报方案；云量统计方案的代表性工作为Sommeria and Deardorff(1977)；而统计动力预报方案的代表性工作为Tompkins(2002)。很多学者对大气模式中的云量问题进行了多方面的探索。Teixeira(2001)研究低云量与相对湿度的关系，从一个稳定的云量预报方程出发，得到了一个关于亚热带边界层的云量诊断方程。Gu et al (2003)从云的光学性质出发，改进了UCLA(University of California, Los Angeles) AGCM模式(Atmospheric General Circulation Model)中的云辐射方案，对全球总云量的计算提高了5%的准确率。戴福山等(2004)提出了一个基于统计的低云参数化方案，用于CCM3(Community Climate Model)模式后显著增强了对大洋东部冷海域低云云量的模拟。郑晓辉等(2013；2016)在GRAPES_Meso模式中引进了欧洲中期天气预报中心(ECMWF)的云量诊断方案并进行了部分优化，提高了模式的预报准确率。随着云计算研究的不断深入，云顶高度、云顶气压、云顶温度、云量、云光学厚度等云参数的计算过程越来越重要。云量对辐射过程具有极其重要的影响，而云顶高度是区分云类型的重要标准之一(宇路和傅云飞，2017)。降水概率与云参数相关性较高，随着云顶温度降低、云光学厚度及云顶粒子平均尺度增加而增加(桂海林等，2019)。对流初生阶段，云顶高度在短时间内快速升高，云顶温度快速降低(周鑫等，2019)。研究表明，云参数的变化可以体现大气运动的变化，对未来天气变化具有先导性价值。鉴于全球三维观测系统的局限性，数值预报模式中这些云参数的分析和计算仍然具有一定的挑战性(Miller et al, 2014)。

近年来，随着遥感技术的迅猛发展，观测云的手段变得越来越多样化。目前云观测主要有卫星红外可见光遥感、卫星微波遥感、云高仪、偏振雷达、星载云雷达、全天空成像辐射仪等云观测手段(韩成鸣等，2015)；地基和空基雷达可以精确地获得高时空分辨率的云水平和垂直结构，毫米波雷达的波长更接近小粒子尺度，可以探测云的各种特性，以及宏观和微观结构。由于云随着时间、空间变化非常迅速多样, 因此，基于卫星和雷达探测得到的资料并不能获取全面的云信息。随着航空业务上的需求增长，对云底高度、云顶高度、云顶温度、云顶气压、云光学厚度等云属性进行更为精确的预报变得越来越重要。由于缺乏广泛分布的云观测设备，航空业务上对于各种云属性的预报需求仍是一种挑战。

越来越丰富的卫星观测资料为诊断分析云计算方案中部分云参数的准确性提供了观测依据；借助于卫星资料发现云计算方案的误差，进而对其优化改进，为研究云计算方案提供了一种新的手段和方法。本文尝试将一些云变量，如云顶温度、云顶高度等相关物理量作为输出变量，与卫星遥感可得到的资料进行比对，从而发现现有模式中云计算方案的不足之处，通过修改相关云方案，以期得到更为准确的云变量，为GRAPES_Meso模式云计算方案的进一步完善提供有益的参考。

1 资料与云计算方案 1.1 资料

美国国家环境预报中心(National Centers for Environmental Prediction，NCEP)每日四次的再分析资料(水平分辨率为0.5°×0.5°)，作为模式初始场和侧边界条件。

用于分析模拟结果的(准)观测资料包括：①日本气象卫星(Himawari-8)的0.05°×0.05°分辨率云产品，要素包括云顶高度和云顶温度，资料来源于：日本宇宙航空研发机构(Japan Aerospace Exploration Agency，JAXA)，ftp://ftp.ptree.jaxa.jp/pub/himawari/L2/CLP/bet/；②风云二号气象卫星0.1°×0.1°分辨率的逐小时相当黑体温度(TBB)产品、总云量(CTA)产品及卫星云图，资料来源于：国家卫星气象中心，http://www.nsmc.org.cn/NSMC/Home/Index.html；③我国多普勒天气雷达反射率因子三维组网拼图资料；④ECMWF再分析云量资料，包括高、中、低云量，空间分辨率为0.125°×0.125°，资料来源于EC官网：https://apps.ecmwf.int/datasets/；⑤全国加密站逐小时地面2 m温度资料，约为2 600个站，其中包括站号、经度、纬度以及地面2 m温度，由中国气象局数值预报中心提供；⑥国家站辐射逐小时资料数据集，包括中国99个站的总辐射(曝辐量)、站号、经度、纬度、站名等，由全国各级气象台站进行质量控制，资料来源于国家气象业务内网。

1.2 云计算方案

现有GRAPES_Meso模式使用的是从ECMWF模式引进的诊断云方案，该方案主要公式如下：

$ {C_{\rm{u}}} = \min \left[ {0.8, \max \left({0.0, 0.125\ln {P_{\rm{r}}} - 1.5} \right)} \right] $

(1)

$ C_{\mathrm{c}}=\left\{\begin{array}{ll} 0.4 C_{\mathrm{u}} & C_{\mathrm{u}} <0.4 \\ \max \left[0.4 C_{\mathrm{u}}, 2\left(C_{\mathrm{u}}-0.3\right)\right] & C_{\mathrm{u}} \geqslant 0.4 \end{array}\right. $

(2)

$ C_{\mathrm{g}}=\left(\frac{R H-C R H}{1-C R H}\right)^{2} $

(3)

$ C_{\mathrm{T}}=\min \left[1.0, \max \left(0.0, C_{\mathrm{c}}+C_{\mathrm{g}}\right)\right] $

(4)

式中：P_r为调用两次辐射方案之间的对流降水率，单位：mm·s^-1; C_u为计算积云量的中间量，C_c为积云量；C_g为利用相对湿度等变量计算得到的格点云量；RH为相对湿度；CRH为相对湿度阈值，不同模式中可能略有不同(Slingo，1987)，GRAPES模式中其范围在0.7~0.9，与所在模式层高度相关；C_T为总云量，为积云量C_c与格点云量C_g相加所得。

2 云量计算方案中问题的发现

由于云变量观测的困难和稀缺，特别是云内部变量观测的缺失，人们经常以雷达等地基观测大致确定云底变量，而用卫星等空基观测大致确定云顶变量的大小。利用云顶变量可以用卫星直接观测或反演的特征，首先对GRAPES_Meso模式云计算方案的云顶部分变量进行诊断分析，以发现云计算方案存在的问题。

本文选取了2018年5月5日和7月5日两次降雨天气过程，对其进行了数值模拟，对模式计算的相关云顶变量进行了输出，并与卫星观测得到的对应云顶变量进行了对比分析。试验所用模式为GRAPES_Meso 4.1.2.1版本，美国NCEP的GFS资料(水平分辨率为0.5°×0.5°)作为模式预报的初始场和侧边界条件，将雷达资料及FY-2卫星资料(包括相当黑体温度数据和总云量数据)加入模式的云分析过程中。模式水平分辨率为5 km，垂直分层49层，模式层顶高度为28 000 m。物理过程参数化方案做如下选择：WSM6微物理过程方案，RRTM长波辐射方案，Dudhia短波辐射方案，Monin-Obukhov近地面层方案，Noah陆面过程方案，MRF边界层方案以及KFeta积云对流参数化方案。分别以2018年5月5日00时(UTC, 下同)和7月5日00时作为模式的初始积分时间，时间步长取为60 s，共积分24 h。

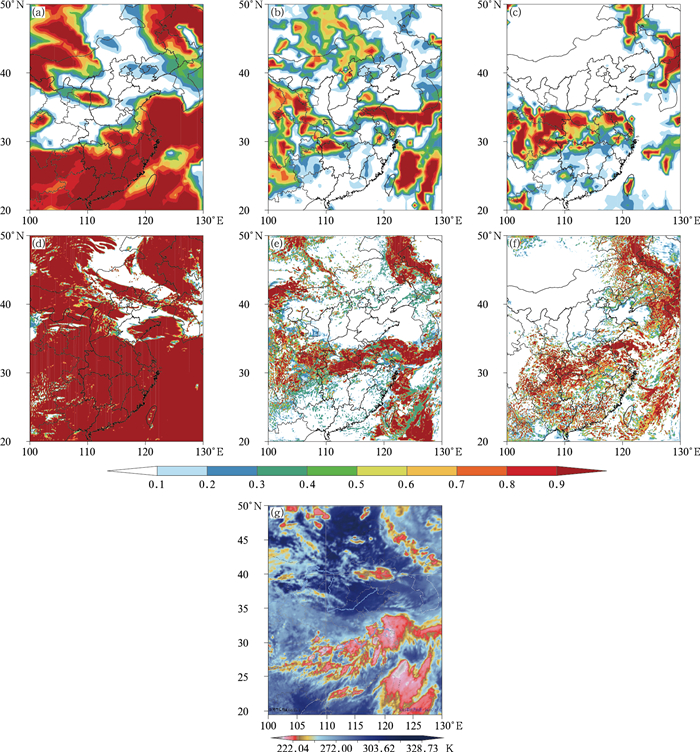
2.1 云量对比

图 1为2018年5月5日06时EC再分析(准观测)和模拟的高云、中云和低云的云量分布以及卫星云图实况。对比图 1a和图 1d, 1g可知，模拟的高云云量明显偏多，特别是在华南和南海北部，空报了大片的高云；对比中云(图 1b, 1e)，模拟的中云的范围和分布与EC再分析比较一致，但模拟的密闭云区的云量不够密实，即比EC的云量少一些；对比低云(图 1c, 1f)，模拟低云的云区(图 1f)比EC再分析的云区范围偏大，而密闭云区云量偏少。总起来看，计算的中低云的范围与卫星观测(图 1g)相比大致相符。

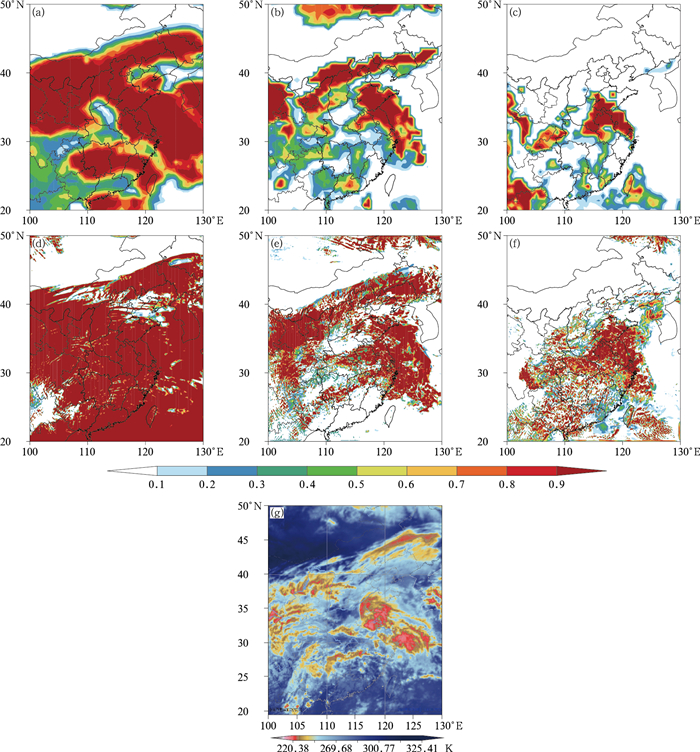
图 2为2018年7月5日06时EC再分析(准观测)和模拟的高云、中云和低云的云量分布和卫星云图实况，对比图 2a和图 2d, 2g可知，模拟的高云云量明显偏多，特别是在华北和江淮北部，空报了大片的高云；对比中云(图 2b, 2e)和低云(图 2c, 2f)与图 1分析结果相类似。

从以上初步分析可知，在目前的云计算方案中，模拟的高云云量偏多，而模拟的中低云密闭云区云量偏少。

利用卫星资料可以得到大气中接近观测的云顶高度和温度，这为研究和改进云顶变量计算方案提供了可能。为此，本文对模式计算的云顶温度和高度进行了诊断和分析。为避免图表过多，以下仅给出2018年5月5日个例的结果。

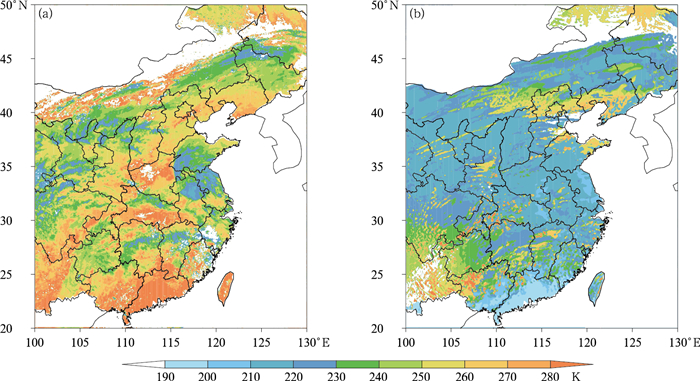
2.2 云顶温度对比

图 3为2018年5月5日06时卫星观测和模式计算得到的云顶温度分布。由图可知，模式模拟的云顶温度在我国的西南地区和华北北部区域与卫星观测较接近，但也存在偏低现象；其他区域模拟的云顶温度是明显偏低的，这说明模式关于云顶的计算存在较大的误差，需要对云顶温度计算进行优化和改进。

2.3 云顶高度对比

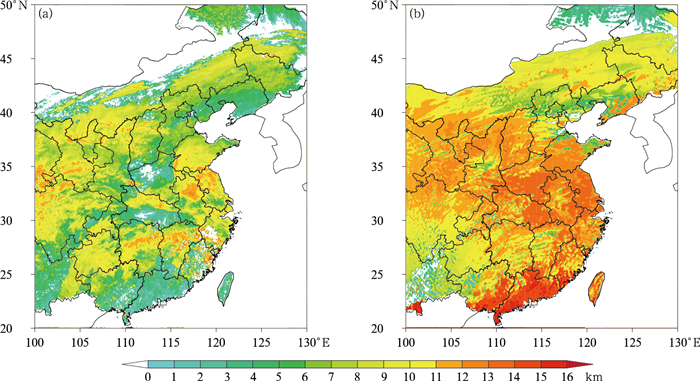
图 4为5月5日06时卫星观测和模式计算得到的云顶高度分布图。由图可知，模式模拟的结果在我国的西南地区和华北北部区域与卫星观测较接近，但也存在偏高现象；其他区域模拟是明显偏高的，这说明模式关于云顶高度的计算存在较大的误差，需要对云顶高度的计算进行优化和改进。

3 云计算方案的优化

从上面分析可以看出，模式现用的云计算方案中，存在三个问题：(1)计算的高云云量偏多；(2)云顶高度偏高；(3)云顶温度偏低。对其他天气个例的模拟计算也存在这三个问题，这里不再详述。

针对存在的问题，对云计算的原理和公式进行了解读，对计算公式进行了优化改进。并进行多次数值试验后发现，以上计算误差主要与高云的格点云量计算有关，其中相对湿度的计算是导致云顶偏高的主要原因。原方案中相对湿度的计算公式为：

$ R H=Q / {{Q}_{\rm{s}}} $

(5)

$ Q_{{\rm{s}}}=0.622 e s /(p-0.378 e s) $

(6)

$ \mathit{es} = \left\{ {\begin{array}{*{20}{l}} {6.1078\exp \left[ {\frac{{17.2693882(T - 273.16)}}{{T - 35.86}}} \right]}\\ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(T \ge 273.15)\\ 6.1078\exp \left[ {\frac{{21.8745584(T - 273.16)}}{{T - 7.66}}} \right] \end{array}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(T < 273.15)} \end{array}} \right. $

(7)

式中：RH为相对湿度，单位：%；Q为比湿，Q_s为饱和比湿，单位：kg·kg^-1；p为大气压，es为饱和水汽压，单位：hPa；T为温度，单位：K。其中饱和水汽压的计算采用了Tetens(1930)经验公式。目前国际上公认的饱和水汽压方程为Goff-Gratch公式(Goff, 1957)，而在0℃以下，Tetens公式与Goff-Gratch公式的相对误差随温度降低而逐渐增大(Mokdad et al, 2012；Xu et al, 2012)。虽然Goff-Gratch公式最为准确，但由于其过于繁琐，并不适用于本模式，因此本试验采用WMO(1996)在第六版《气象仪器和观测方法指南》中公布的饱和水汽压计算公式替换原方案中的公式，从而对原方案中云计算部分进行优化，具体修改公式如下：

$ f(p)=1.0016+3.15 \times 10^{-6} p-0.074 p^{-1} $

(8)

$ e s=\left\{\begin{array}{c} f(p) 6.112 \exp \left[\frac{17.62(T-273.15)}{T-30.03}\right. \\ (T \geqslant 273.15) \\ f(p) 6.112 \exp \left[\frac{22.46(T-273.15)}{T-0.53}\right. \\ (T <273.15) \end{array}\right. $

(9)

式中：p为大气压，单位：hPa；f(p)为与大气压p有关的函数；T为温度，单位：K；es为饱和水汽压，单位：hPa。此外，结合观测可知180 hPa以上云量极少，因此将模式180 hPa以上的云量计算阈值最大值设为0.1，并经过多次数值试验后修改了该方案中影响云中水凝物含量计算的参数。

4 云量新方案的数值试验

利用新的云计算方案对2018年5月5日天气过程进行了数值模拟，并与原方案计算的云进行了对比分析。以下图表中OBS为观测值，CTL为原方案的模拟结果，TEST为改进方案的模拟结果。

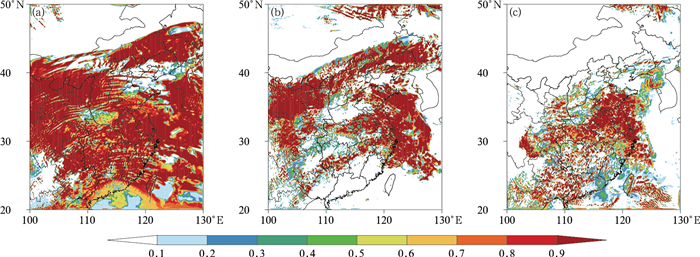
图 5为模拟的高云、中云和低云的云量分布。对比图 5与图 1可知，新的云量计算方案计算的高云(图 5a)与原来方案计算结果(图 1d)相比，在华南和南海北部原方案中空报的高云云量明显减少，更接近于EC再分析的高云云量分布；新旧方案的中云和低云云量变化不明显。

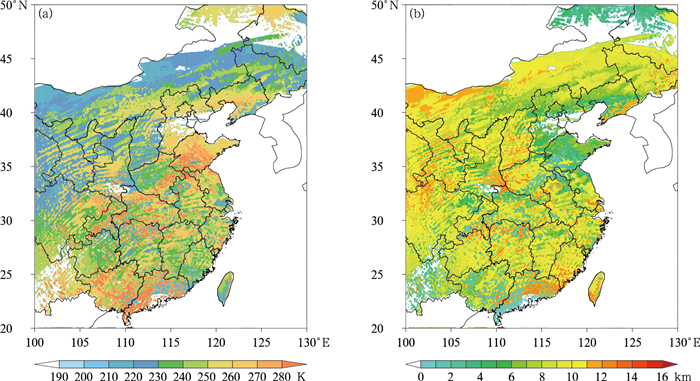
图 6为模拟的云顶温度和云顶高度。对比图 6a与图 3对应的云顶温度可知，新的云量计算方案计算的云顶温度明显比原来方案计算的结果更接近观测，部分修正了原方案中计算的云顶温度过低的误差；对比图 6b与图 4对应的云顶高度，发现新方案计算的云顶高度明显比原来方案计算的结果更接近观测，部分修正了原方案中计算的云顶高度过高的误差。

为定量描述云计算方案改进前后云顶温度和高度的变化情况，制作了两个要素的预报均方根误差随时间变化表(表 1)。由表 1可知，改进后的云顶温度和云顶高度均方根误差均小于改进前的数值；同时也能看出，虽然改进后的均方根误差有明显降低，但仍然有较大的误差，这是由于数值模式在中高层层数较稀疏，各层之间距离较大，由此造成模式中高层计算的云顶温度和高度会出现较大误差，同时云计算方案本身也不够完善。要更好地解决这个问题，需要数值模式垂直分层不断加密和云计算方案不断完善。

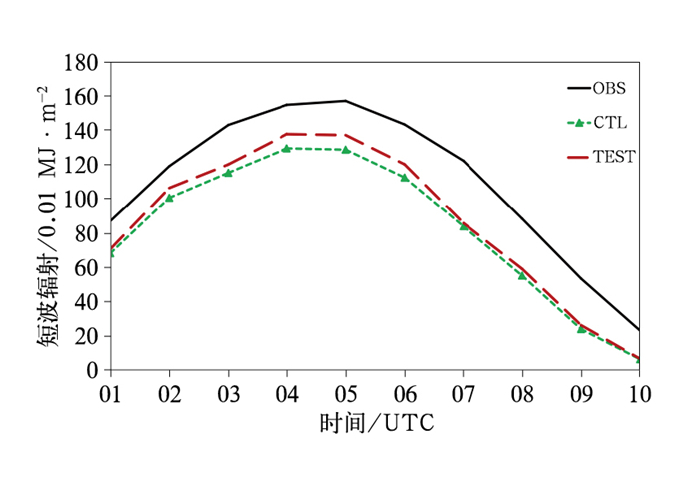
云量计算方案的优化改进，必然对模式大气辐射的计算产生影响。为此，本文给出了区域平均的模式计算和观测得到的总辐射曝辐量(短波辐射)随时间演变(图 7)。由图可知，新方案计算(红虚线)和旧方案计算(绿虚线)的短波辐射较实际观测值都偏低，但新方案计算值都大于旧方案的值，更接近实际观测值。这说明云计算方案经过改进后对大气短波辐射的计算也得到了改善。

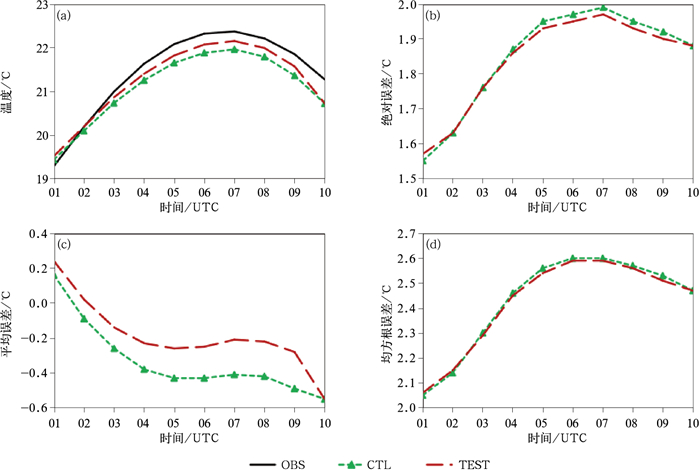
前面重点分析了高空云变量的变化，而高空云的变化也必然引起地面温度的变化，因此针对2 m温度进行分析。图 8为模式区域的2 m温度、绝对误差、平均误差和均方根误差随时间变化。由图 8a可知，预报的2 m温度在积分2 h后都低于观测值，但都表征出与观测值一致的日变化特征，新方案预报的温度更接近观测值；由图 8b, 8c, 8d分析2 m温度的误差变化，同样也可以得到新方案在积分2 h后，其2 m温度的平均误差更接近0，绝对误差和均方根误差均小于原来方案的预报结果。2018年7月5日的个例模拟分析结果与之相似，这里略去。

综合以上分析可以认为，云量方案经过改进后，模式计算的高云云量、云顶温度和云顶高度都更接近观测值，即减小了模式预报误差。

5 结论与讨论

通过对两次降雨天气过程的模拟，重点对比分析了2018年5月5日卫星观测和模式模拟在云量、云顶温度和云顶高度的差异，发现GRAPES_Meso模式在云计算方案中存在的问题，针对这些问题对方案进行了初步研究和改进，主要结论如下：

(1) GRAPES_Meso模式现用的云计算方案中，模拟的高云云量偏多，而模拟的中低云密闭云区云量偏少；模式模拟的云顶温度明显偏低，而模拟的云顶高度明显偏高。

(2) 针对模式云计算存在的问题，对云计算的原理和公式进行了解读，对计算公式进行了优化改进。

(3) 采用改进的云计算方案后，高云云量偏多问题得到了明显改进；模式模拟的云顶温度明显偏低和云顶高度明显偏高问题也得到了极大缓解或优化改进。

本文以卫星观测资料为基础对云量计算方案的优化进行了初步探索和试验，取得了令人鼓舞的结果。本文的研究是初步的，由于文章篇幅和计算量的限制，文章只分析了两个个例，重点给出了2018年5月5日的结果。随着越来越丰富的观测资料的出现，将为模式物理过程的诊断和改进提供更可靠的资料基础和修改依据，这将为模式物理过程的精细化和正确性奠定坚实的研究基础，这种方法将会越来越多地应用于模式物理过程的研发和评估中。