2. 北京市气象台,北京 100089;
3. National Center for Atmosphereic Research, Boulder, USA
2. Beijing Meteorological Observatory, Beijing 100089;
3. National Center for Atmospheric Research, Boulder, USA
数值预报模式的直接输出结果受很多因素影响会产生不确定性,这些不确定性可能来源于初始条件(丑纪范,2007)、模型建立过程中对多物理过程描述或对多个模型集合时缺乏细节或未描述地形、相关地理信息等(康红文等,2012),也存在随机参数化过程等引入不确定性;侧边界条件和下边界条件设定时都会引入不确定性,比如下垫面条件,城市、非城市地区,以及海拔高度等在不同地区有不同问题(桑建国等,1992)。模式的预报结果与实况观测结果相比存在很大误差,因此对模式预报进行有效订正提高产品的业务应用性能是一项重要的研究课题。
目前,数值预报的订正方法有很多种,主要有模式输出统计(MOS)、完全预报法(PP)、卡尔曼滤波(KLM)、人工神经网络(ANN)、相似预报法等(赵声蓉,2006;吴君等,2007;张庆奎等,2008;Delle Monache et al, 2011;吴启树等,2016)。每种方法都有其优势的地方,而相似预报法从寻找过去历史资料中的相似天气形势或相似个例,来对当前的预报进行订正,是气象学中的经典方法,是较接近预报业务思路的方法。Lorenz(1965;1969)认为大气可预测性是由于自然发生的相似的天气形势决定的,认为在全球范围内选取完全一样的天气形势需要1030年,然而在大范围区域(例如整个北半球)找到观测误差范围内的2个相似流体(天气形势)是可以在相对短的时间内实现。那么在10~100年的观测时段内,针对某一有限区域,假设2~3个自由度,寻找相似个例的概率会很大。基于这样的理论背景,研究者们对相似方法在气象和气候学上的应用也较为广泛。Bergen and Harnack (1982)运用了多个相似预报的加权平均;Shabbar and Knox (1986)使用n天大气状态综合选相似。上述工作均是使用相似来做长期预报,对于短期天气预报的应用也很多。Van den Dool (1987;1989;1991)系统地研究了相似和反相似的预报性能和使用前景,并指出可用区域取代全球找相似来克服资料少的困难,关于区域性相似的问题也被Robber and Lance (1998)详细讨论。鉴于取样单个相似的不确定性,可通过选取一组相似来实现集合概率预报(Kruizinga and Murphy, 1983;Gruza and Esther, 1993),基于统计学方法的相似预报在短期预报中的效果也较好。到目前为止,美国已实现了相似预报技术在业务上的应用,我国也有很多相关的研究(鲍名等,2004;陈凯,2014;周海,2009;任宏利,2006)。鉴于对相似天气形势的判断有难度,Delle Monache et al(2011)利用寻找相似的气象要素,即寻找当前预报与过去预报相似的气象要素,再将这些相似的历史个例的观测值来校正当前预报,利用最优集合(analog ensemble,AnEn)预报订正方法对美国西部地区的风和温度预报进行了订正并取得了较好的效果,模式预报的偏差得到了有效订正。
目前国内业务上采用的温度预报订正方法主要是基于MOS的,包括一元和多元线性回归等,对温度的订正效果较好,为业务应用提供了较好的参考,这些方法是根据温度在时间上的连续性以及与其他气象要素的相关性对模式结果进行误差订正的;就应用效果而言,各方法均有其占优势的地方,很难找出一个完美的、在所有时段所有站点都应用效果很好的方法,因此,开发不同的温度预报订正方法给业务应用提供参考有一定的研究意义。针对AnEn方法在偏差订正方面的研究,本文拟采用该订正方法对北京地区基于ECMWF预报的日最高气温和日最低气温进行订正,测试训练日期长度、环境变量权重、相似天气个例数等变量,寻找优化的参数变量值,完成参数的本地化,并分析AnEn的实际应用效果尤其是在山区的订正效果。
1 资料本文采用2012年1月1日至2017年8月31日ECMWF细网格逐3 h(或6 h)的资料(0~72 h时效内的时间分辨率为3 h,72~168 h的分辨率为6 h),水平分辨率为0.125°(2015年1月15日之前为0.25°),每日08和20时(北京时)两时次,预报时效为0~168 h。选取2 m气温、10 m u风、10 m v风、2 m露点温度等要素预报作为环境变量。
为确保实况资料的可靠及完整性,本文采用北京地区2012年1月1日至2017年9月6日国家基本气象站(15站)及自动站(274站)逐5 min的地面气温资料作为实况。
预报员的主观预报数据采用与ECMWF同时间段内的资料,每日两次,即08和20时起报的0~168 h内的日最高气温、日最低气温预报。为了准确衡量AnEn在实际应用中的预报订正效果,本研究采用与业务应用时效一致的方案,即20时的数值模式预报资料对应当日08时的主观预报,而08时的数值模式预报对应前一日20时起报的主观预报,并将起报时刻开始至12 h内的温度预报剔除不做订正和检验(该时段资料预报员无法参考)。
2 方法 2.1 最优集合预报订正技术AnEn旨在改进由于数值模式产生的不确定性引起的误差,尤其是误差中的系统误差(偏差)部分。它采用寻找过去一段时间内的相似个例集合,并对这些相似个例进行加权平均来实现对误差的订正,达到减小模式预报误差的目的,获得一个更接近实况观测的结果。本研究采用下述方法进行最优的选择(Delle Monache et al,2011):
| $ {d_t} = \left| {{f_t} - {g_t}} \right| = \sum\limits_{v = 1}^{{N_v}} {\frac{{{w_v}}}{{{\sigma _{fv}}}}} \sqrt {\sum\limits_{k = - t}^t {{{\left({f_{t + k}^v - g_{t + k}^v} \right)}^2}} } $ | (1) |
式中,dt为当前预报与过去预报的接近程度(即相似程度);ft为t时刻对应的预报值;gt为t时刻对应的过去的预报值。wv为环境变量对预测要素的权重,可以通过历史资料进行优化;σfv在固定权重配置时设为1,第v个环境变量的预报值f的方差;Nv为环境变量的总数;t+k时刻对应过去的数据的预测值;k为预测窗的一半(用整数表示):可以自行设定,t=1,则k为-1, 0, 1。
本文针对2 m气温的预报,先确定与温度相关的环境变量:过去的2 m气温、10 m风速、10 m风向、2 m露点温度等;对这些环境变量的过去的预报和当前的预报根据式(1)计算相似距离dt,即对每个环境变量求当前预报和过去预报之间的差,再将不同变量按照权重求和,最后得出当前预报与过去预报的差别程度,即距离dt,根据dt排序,筛选出dt最小的那些值,即为最优的相似个例集。
针对选取的最优预报个例集,进行集合计算(Delle Monache et al,2011):
| $ F_t^\prime = \sum\limits_{i = 1}^N {{r_i}} {O_{i, t}} $ | (2) |
| $ {r_i} = \frac{{{d_{{t_i}}}}}{{\sum\limits_{i = 1}^N {{d_{{t_i}}}} }} $ | (3) |
式中,F′t为t时刻的预报订正值;N为选取的最优集合的数量;Oi, t为t时刻预报的最优个例的观测值;ri为第i个观测的权重,即距离t时刻越近则权重越大;dti为t时刻第i个距离值,由式(1)计算出来。
将日最高气温和日最低气温分别进行上述计算,寻找历史资料中ECMWF模式资料的相似个例[式(1)],并将这些最优个例的实况值加权平均[式(2)和式(3)],作为对当前时刻的ECMWF预报的订正值,即AnEn的预报;从原理上看,AnEn是利用历史资料的观测来校正当前数值预报的偏差。
2.2 数据处理方法为提高计算效率同时不降低预报质量,训练集数据采用滑动方式(吴启树等,2016),即将预报日的前n天与前一年的后n天资料作为训练期,随预报日滑动取样。检验日即为预报日。
实况2 m气温采用5 min数据提取成日最高气温和日最低气温(根据实际业务应用标准,日最高气温取02时至次日02时的最高温度,日最低气温取20时至次日20时的最低温度),数据缺失量大于20%时将该站该日从训练集剔出,数据量缺失小于20%时采用内插方法补足数据。
ECMWF模式的格点场资料插值到气象站时,综合考虑插值准确程度和计算效率,本研究采用最近邻距离插值方法插值到气象站上,同时利用15 m的数字高程模型(DEM)资料对气象站邻近的4个ECMWF格点的高程进行对比,如果该站与周围格点高度相差100 m以上,则该格点不参与插值,以此确保插值到站点后的值接近气象站的实况值。
2.3 检验方法为了评估AnEn的预报效果,本研究对2016年9月1日至2017年8月31日的效果用均方根误差(RMSE)、偏差(BIAS)、温度预报准确率(FA)和温度预报技巧评分(TSS)来检验效果;同时对2016年(训练集为2014—2015年)和2015年(训练集为2013—2014年)的主客观预报效果进行时间上的检验分析;对2016年9月1日至2017年8月31日的276个自动站进行空间效果的检验。其中检验计算公式如下:
| $ RMSE = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{O_i} - {A_i}} \right)}^2}} $ | (4) |
| $ BIAS = \bar A - \bar O $ | (5) |
其中,
| $ \bar A = \frac{1}{n}\sum\limits_{i = 1}^n {{A_i}}, \;\bar O = \frac{1}{n}\sum\limits_{i = 1}^n {{O_i}} $ | (6) |
| $ {F_2} = \frac{{{n_2}}}{n} \times 100\% $ | (7) |
| $ TSS = \frac{{{T_{{\rm{mean }}}} - {T_{{\rm{meaf }}}}}}{{{T_{{\rm{mean }}}}}} \times 100\% $ | (8) |
式中,Oi为i时刻的实况值,n为样本量,Ai为i时刻的AnEn估计值,A和O分别为AnEn的均值和实况的均值。F2为温度预报与实况值的误差不超过2℃的百分率,n2为不超过2℃的样本量。TSS为预报技巧评分,Tmean和Tmeaf分别为ECMWF和对比预报的平均误差。
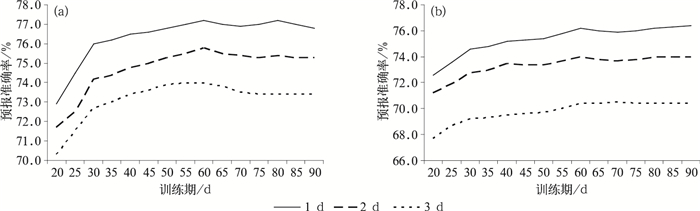
3 方案对比与改进为了提高算法的计算效率,首先对训练日期长度进行试验,结果表明,60 d以后结果波动变小(图 1),为了在保证预报准确率的基础上提高效率,本文以60 d为训练期,即采用预报日前60 d,预报日去年的后60 d(以此类推)的资料作为训练样本,对环境变量和权重参数进行优化:
|
图 1 日最高气温(a)和日最低气温(b)不同训练期的预报准确率变化 Fig. 1 The change of prediction accuracy rate for different training days for maximum temperature (a) and minimum temperature (b) |
方案1:统一选用4个环境变量(Delle Monache et al,2011),选取20个相似值,固定权重,即设置2 m气温、10 m风速、10 m风向和2 m露点温度的权重分别为0.7, 0.1, 0.1, 0.1。
方案2:由于6—11月中霾和降水天气相对较多,针对这些天气的相似案例较少,则对12月至次年5月采用20个相似值,6—11月选取15个相似值,即选用式(3)中对dt排序后的前20或15个历史个例,固定权重配置(如方案1)。
方案3:优化权重选取上一年同期的1、3、6个月,结果表明1个月的优化权重不稳定,综合效果较差,而3和6个月的优化差距不大,但6个月的优化更稳定。本文仅列出6个月的优化效果。
方案4:在方案2的基础上延长训练期时间,即将2012年1月1日至2016年8月31日的资料作为训练集。
4 检验效果 4.1 几种方案的结果对比对2016年9月1日至2017年8月31日的逐日结果进行检验,固定权重下两种方案的对比(表 1)可以看出,不论是日最高气温还是日最低气温,AnEn的效果均比ECMWF原始预报的均方根误差和预报偏差有不同程度的改进,其中方案2的改进效果更好一些,相对于ECMWF的预报技巧提高了10%以上。而在优化环境变量的权重之后,三种参数方案有所差距,以月为周期的权重配置波动性较大,稳定性最差,而以3和6个月为周期的权重配置较为稳定,结果相差不大,表 2仅列出6个月下优化效果。与优化环境变量权重相比,延长训练期的时间对预报质量的提高更为显著(表 2),日最高气温的订正效果好于日最低气温,预报技巧总体分别提高了15.4%和12.4%,且预报时效越短订正效果越好;方案4对日最低气温的RMSE改进效果不如方案2的效果好,但BIAS比方案2普遍低,可能是由2015年1月15日之后ECMWF模式有所调整,分辨率不同造成的,由此虽然历史资料的延长可以减小预报偏差,但由于资料前后不一致导致的随机误差也较大,而日最高气温的RMSE和BIAS在方案4中是最小的;相比预报员的主观预报,不论是日最高气温还是日最低气温,在4~7 d的中期预报中AnEn的预报技巧比预报员分别提高了3.5%和6.3%,而1~3 d的日最高气温的预报AnEn比ECMWF提高18.4%, 而相比预报员有2.0%的差距,日最低气温在1 d的AnEn预报比ECMWF提高12.5%,但与预报员相比有一定的差距。
|
|
表 1 不同方案之间的日最高气温与日最低气温预报检验 Table 1 Prediction tests of daily maximum temperature and minimum temperature for different plans |
|
|
表 2 不同优化权重配置下的日最高气温与日最低气温预报检验及与主观预报的对比 Table 2 Comparison of daily maximum temperature and minimum temperature between AnEn and subjective predictions for different optimal weights |
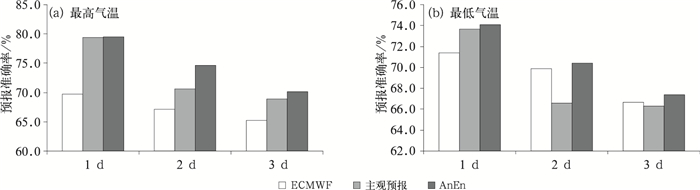
为验证AnEn方法对客观温度预报的稳定性,本文从时间和空间上对该方法进行了进一步检验(图 2和图 3)。图 2为2016年的预报准确率检验,AnEn的效果都比预报员高出0.1%~4.5%,在时间上表现出良好的稳定性。
|
图 2 2016年ECMWF、主观预报和AnEn对日最高气温(a)和日最低气温(b)的预报准确率对比 Fig. 2 Comparison of ECMWF, AnEn and subjective predictions of daily maximum temperature (a) and minimum temperature (b) in 2016 |
|
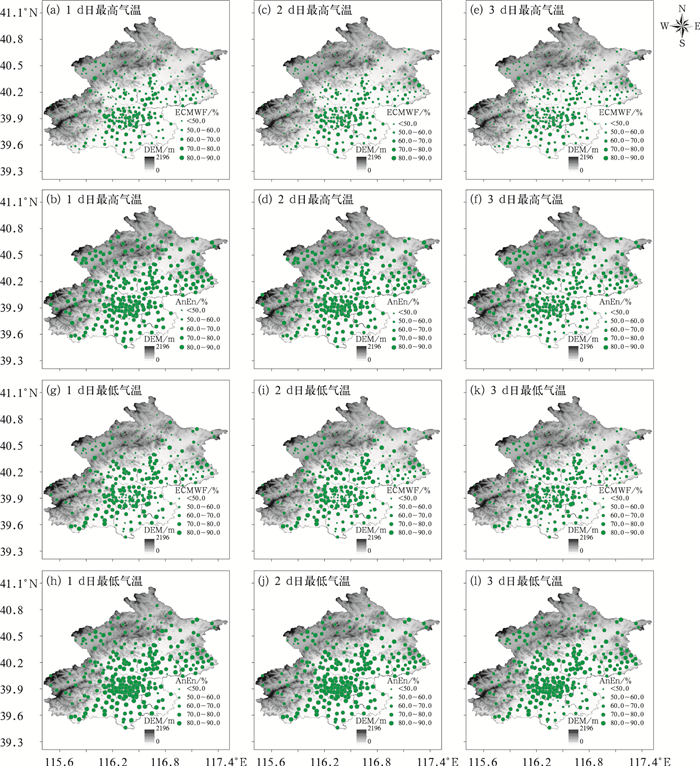
图 3 2017年北京地区274个自动站的ECMWF(a,c,e; g,i,k)和AnEn(b,d,f; h,j,l)对最高气温(a, c, e; b, d, f)和最低气温(g, i, k; h, j, l)的预报准确率对比 (DEM为高程信息) Fig. 3 The comparison of ECMWF (a, c, e; g, i, k) and AnEn (b, d, f; h, j, l) predictions for maximum temperature (a, c, e; b, d, f) and minimum temperauter (g, i, k; h, j, l) of 274 stations over Beijing in 2017 (DEM means digital elevation model) |
从空间上看,北京地区274个自动站的预报准确率AnEn都比ECMWF有了较大提高,1~3 d的日最高气温预报准确率分别提高了19.0%、19.8%和16.5%,对应的日最低气温预报准确率分别提高了14.0%、13.3%和10.2%。日最高气温的RMSE和BIAS分别由2.526和-1.616减至2.016和-0.212,日最低气温的RMSE和BIAS分别由2.474和0.266减至1.931和0.009,预报偏差几乎减至无偏,表明AnEn对于预报偏差的订正效果较好。图 3表明,在ECMWF的预报质量较差(预报准确率通常低于50.0%)的地区,大部分都是地形较为复杂和受边界层影响较大的地区,AnEn体现了较好的订正能力。未来采用合适的插值方案,AnEn可以从基于站点的预报向智能网格预报业务应用,提高智能网格客观预报质量。
4.3 最优方案的效果及与主观预报的对比根据方案4对1~3 d的气温预报进行分月详细分析,虽然预报技巧评分比ECMWF直接输出高,但是总体看无论最高还是最低气温在5、6和10月的预报技巧较差,这可能跟大气环流的季节性调整有关。但逐日分析发现在雾-霾、阴雨等天气发生的时间段内,AnEn的订正效果虽比ECMWF直接输出提高不少,但预报技巧还不尽人意。这也是下一步要解决的问题。
5 结论和讨论(1) 对AnEn的参数本地化中,将滑动训练期设置为60 d既能保证预报质量,同时又能提高计算效率;对相似个数的选取进行区分比不区分效果好,而延长训练时间(增加训练集的历史资料)比优化环境变量的效果更好地减少预报偏差,这一点与吴启树等(2016)在对最佳训练期的周期优化时的研究结论相似,也与Junk et al(2015)的结论相似,AnEn的环境变量权重优化周期采用的时间短,则结果越不稳定;而延长周期时间,保证了预报质量的稳定性,但同时也会平滑掉转折性天气。
(2) 从对2015—2016年的检验以及对北京地区274个自动站的效果检验可以看出,AnEn方法对客观温度预报的订正效果在时间和空间上均表现出较好的稳定性,它可以减小模式预报结果的偏差,尤其是对山区地形复杂区域(空间评分前述是2017年),对模式由于缺乏地形和海拔信息的描述以及边界层日变化描述而导致的偏差订正效果较好,可以较大程度地提高预报质量。未来采用合适的插值方案,AnEn可以从基于站点的预报向智能网格预报业务应用,提高智能网格客观预报质量。
(3) 相对于MOS方法,AnEn的优势在于对误差中的偏差定义清晰,对于固定误差即偏差明显的地方如山区AnEn的订正效果明显;对于夜间的温度(本研究为日最低气温),受扰动较少,偏差占优势的时间段的订正效果明显。因此,该方法在业务上有一定的应用前景。
最优预报技术方法不考虑原始数据初始分布状态,容易与其他方法结合,除本文的加权平均方法外,还可以与其他集合方法(如卡尔曼滤波、机器学习等)结合。AnEn算法在客观温度预报订正上的一个缺点是由于天气条件引起的如风起时的非绝热加热效应、局地降水、霾、极端高低温等,AnEn的订正效果较差,而预报员对这些天气的把握能力明显高于AnEn,说明AnEn方法在判断天气形势时仍存在不足,在选取相似个例时采用更多环境变量可以更好地判断天气形势,但由于计算效率的限制,本研究仅选用了4个环境变量来判断相似,如何在保证计算效率的同时采用多变量来定义相似个例是未来的一个研究方向。
鲍名, 倪允琪, 丑纪范, 2004. 相似-动力模式的月平均环流预报试验[J]. 科学通报, 49(11): 1112-1115. Bao M, Ni Y Q, Chou J F, 2004. The experiment of monthly mean circulation prediction using the analogy-dynamical model[J]. Chin Sci Bull, 49(12): 1296-1300 (in Chinese).
|
陈凯, 2014.基于加权KNN算法的降水相似预报方法研究与实现[D].南京: 南京航空航天大学. Chen K, 2014.Research and rea-lization of precipitation forecast based on weighted KNN Algorithm[D].Nanjing: Nanjing University of Aeronautics and Astronautics(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1014061996.htm
|
丑纪范, 2007. 数值天气预报的创新之路——从初值问题到反问题[J]. 气象学报, 65(5): 673-682. Chou J F, 2007. An innovative road to numerical weather prediction—from initial value pro-blem to inverse problem[J]. Acta Meteor Sin, 65(5): 673-682 (in Chinese). DOI:10.3321/j.issn:0577-6619.2007.05.003
|
康红文, 祝从文, 左志燕, 等, 2012. 多模式集合预报及其降尺度技术在东亚夏季降水预测中的应用[J]. 气象学报, 70(2): 192-201. Kang H W, Zhu C W, Zuo Z Y, et al, 2012. Statistical downsca-ling of pattern projection using multi-model output variables as predictors[J]. Acta Meteor Sin, 70(2): 192-201 (in Chinese).
|
任宏利, 2006.动力相似预报的策略和方法[D].兰州: 兰州大学. Ren H L, 2006.Strategy and methodology of dynamical analogue prediction[D].Lanzhou: Lanzhou University(in Chinese).
|
桑建国, 吴熠丹, 刘辉志, 等, 1992. 非均匀下垫面大气边界层的数值模拟[J]. 高原气象, 11(4): 400-410. Sang J G, Wu Y D, Liu H Z, et al, 1992. Numerical simulation of atmospheric boundary layer over inhomogeneous underlying surface[J]. Plateau Meteor, 11(4): 400-410 (in Chinese).
|
吴君, 裴洪芹, 石莹, 等, 2007. 基于数值预报产品的地面气温BP-MOS预报方法[J]. 气象科学, 27(4): 430-435. Wu J, Pei H Q, Shi Y, et al, 2007. The forecasting of surface air temperature using BP-MOS method based on the numerical forecasting results[J]. Sci Meteor Sin, 27(4): 430-435 (in Chinese). DOI:10.3969/j.issn.1009-0827.2007.04.012
|
吴启树, 韩美, 郭宏, 等, 2016. MOS温度预报中最优训练期方案[J]. 应用气象学报, 27(4): 426-434. Wu Q S, Han M, Guo H, et al, 2016. The optimal training period scheme of MOS temperature forecast[J]. J Appl Meteor Soc, 27(4): 426-434 (in Chinese).
|
张庆奎, 寿绍文, 陆汉城, 2008. 卡尔曼滤波方法在极端温度预报中的应用[J]. 科技信息, (35): 811-812. Zhang Q K, Shou S W, Lu H C, 2008. The application of Kalman filter in extreme temperature prediction[J]. Sci Technol Inf, (35): 811-812 (in Chinese). DOI:10.3969/j.issn.1001-9960.2008.35.661
|
赵声蓉, 2006. 多模式温度集成预报[J]. 应用气象学报, 17(1): 52-58. Zhao S R, 2006. Multi-model consensus forecast for temperature[J]. J Appl Meteor Sci, 17(1): 52-58 (in Chinese). DOI:10.3969/j.issn.1001-7313.2006.01.007
|
周海, 2009.动态相似统计方法的改进及其在温度预报中的应用[D].兰州: 兰州大学. Zhou H, 2009.Improving the method of statistical forecast with dynamic analog and its application for temperature forecast[D].Lanzhou: Lanzhou University(in Chinese).
|
Bergen R E, Harnack R P, 1982. Long-range temperature prediction using a simple analog approach[J]. Mon Wea Rev, 110(8): 1083-1099. DOI:10.1175/1520-0493(1982)110<1083:LRTPUA>2.0.CO;2
|
Delle Monache L, Nipen T, Liu Y B, et al, 2011. Kalman filter and analog schemes to postprocess numerical weather predictions[J]. Mon Wea Rev, 139(11): 3554-3570. DOI:10.1175/2011MWR3653.1
|
Gruza G V, Esther Y R, 1993. Potential predictability assessment for analog long-term forecasting[J]. Russian Meteorology and Hydorlogy, 9: 1-7.
|
Junk C, Delle Monache L, Alessandrini S, et al, 2015. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble[J]. Meteor Z, 24(4): 361-379. DOI:10.1127/metz/2015/0659
|
Kruizinga S, Murphy A H, 1983. Use of an analogue procedure to formulate objective probabilistic temperature forecasts in the Netherlands[J]. Mon Wea Rev, 111(11): 2244-2254. DOI:10.1175/1520-0493(1983)111<2244:UOAAPT>2.0.CO;2
|
Lorenz E N, 1965. A study of the predictability of a 28-variable atmospheric model[J]. Tellus, 17(3): 321-333. DOI:10.3402/tellusa.v17i3.9076
|
Lorenz E N, 1969. Atmospheric predictability as revealed by naturally occurring analogues[J]. J Atmos Sci, 26(4): 636-646. DOI:10.1175/1520-0469(1969)26<636:APARBN>2.0.CO;2
|
Robber P J, Lance F B, 1998. The sensitivity of precipitation to circulation details.Part Ⅰ:an analysis of regional analogs[J]. Mon Wea Rev, 126(2): 437-455. DOI:10.1175/1520-0493(1998)126<0437:TSOPTC>2.0.CO;2
|
Shabbar A, Knox J L, 1986. Monthly prediction by the analogue method[J]. Long-Range Forecasting Research Report Series, WMO, Programme on Long-Range Forecasting Research, 2(6): 672-681.
|
Van den Dool H M, 1987. A bias in skill in forecasts based on analogues and antilogues[J]. J Clim Appl Meteor, 26(9): 1278-1281. DOI:10.1175/1520-0450(1987)026<1278:ABISIF>2.0.CO;2
|
Van den Dool H M, 1989. A new look at weather forecasting through analogues[J]. Mon Wea Rev, 117(10): 2230-2247. DOI:10.1175/1520-0493(1989)117<2230:ANLAWF>2.0.CO;2
|
Van den Dool H M, 1991. Mirror images of atmospheric flow[J]. Mon Wea Rev, 119(9): 2095-2106. DOI:10.1175/1520-0493(1991)119<2095:MIOAF>2.0.CO;2
|
 2019, Vol. 45
2019, Vol. 45 
