2. .安徽省气象台,合肥 230031;
3. 南京大学大气科学学院,南京 210023
2. Anhui Meteorological Observatory, Hefei 230031;
3. School of Atmospheric Sciences, Nanjing University, Nanjing 210023
在全球气候变暖的大背景下,暴雨呈现出频发、突发的趋势(王会军等,2010),极端性日益增加,由暴雨引发的洪涝灾害也频繁发生。尤其是淮河流域,具有独特的“漏斗形”地形,上游比降大,降水快速汇流至中下游,但中下游比降小,排水不畅,极易形成洪涝(毕宝贵等,2004;卢燕宇和田红,2015)。因此提升淮河流域的暴雨预报能力、增加洪涝灾害的可预报性是目前研究的热点及难点。
在面向流域的水文气象服务中,数值预报模式在暴雨预报的优势越来越突出,成为业务人员制作流域面雨量的主要依据。为让数值预报产品能够在业务应用中达到最优的预报性能,国内外研究者对多种模式进行了检验、评估(刘静等,2014;叶金印等,2017;朱占云等,2016;董全等,2016)。在模式降水预报性能不断提高的基础上,耦合数值预报降水产品和分布式水文模型用于增长洪水预报有效预见期、提高预报精度已成为可能。欧美等发达国家在多个河流预报中心建立了气象水文耦合预报系统,在实时洪水预报中进一步验证了耦合技术的优越性。在我国,水文模式与气象模式的耦合正在逐步开展(包红军等,2016),甘衍军等(2017)研发了基于CREST(Coupled Routing and Excess Storage)分布式水文模型的暴雨致洪预报系统,应用中国气象局降水业务产品,开展全国逐日洪水预报和区域逐时洪水预报。包红军和赵琳娜(2012)、包红军等(2017)建立了气象水文耦合的淮河洪水预报模型。
虽然国内外学者在数值预报性能评估及洪涝预报方面取得了丰硕的成果,但仍有许多方面有待深入研究。例如以往面雨量预报的评估基本是针对24 h时间尺度降水,较少有对12、6 h时间尺度暴雨量级的面雨量进行评估,特别是可能引发山区中小流域暴洪的3和1 h的短历时强降水,几乎无人对其预报效果进行评估。在气象水文耦合技术方面,降水预报的不确定性和水文模型的不确定性叠加,使得洪涝预报的不确定性被放大,预见期缩短,但目前的研究大多是针对几次洪水过程的可预报性进行评估,较少有基于长时间序列的洪水预报不确定性检验。本文以淮河流域暴雨量级的面雨量为研究对象,选用2015—2017年淮河汛期ECMWF(以下简称EC)、JMA(Japan Meteorological Agency)等全球数值模式及WRF(Weather Research and Fovecasting Model)和INCA(The Integrated Nowcas-ting through Comprehensive Analysis)(Haiden et al,2011; Wang et al,2017)等区域数值模式降水预报产品,使用TS评分、空估率、漏估率等指标对不同时间尺度(24、12、6、3、1 h)的暴雨预报进行评估,以期能准确地把握降水预报性能并加以有效利用。利用评估出的效果最优的降水预报产品驱动分布式水文模型CREST(Wang et al, 2011; Xue et al, 2015),构建王家坝以上的淮河上游分布式洪水预报模型,对比2016—2017年汛期不同预见期内的流量预报和观测流量,进一步评估数值预报产品在增长洪水预见期的作用,探讨洪水灾害的可预报性。
本文对多时间尺度暴雨预报的多模式评估以及对基于模式降水预报的洪涝可预报性的探讨,既能更好地发挥降水预报在防洪抗灾、水资源利用工作中的决策支持作用,又能使防汛决策者充分了解面雨量预报及洪涝预报的不确定性,为其科学决策提供重要的技术支撑。
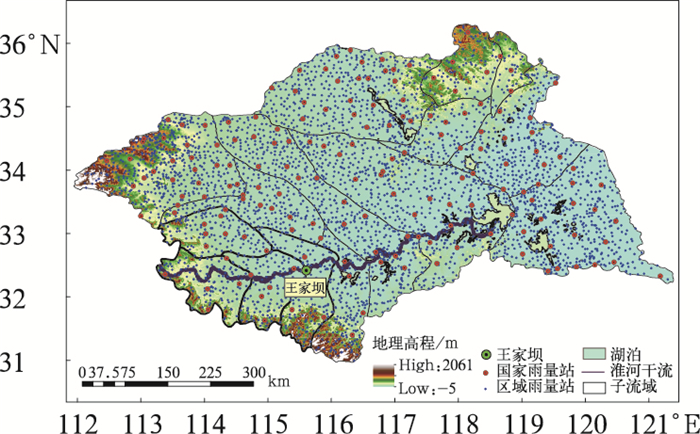
1 研究区概况淮河流域地处长江流域和黄河流域之间,位于30°55′~ 36°36′N、111°55′~ 121°25′E,地跨河南、山东、安徽、江苏四省,流域面积为27万km2。根据淮河流域洪水汇流的特点,结合流域防汛抗旱服务需求,将流域划分为15个子流域(图 1)。
|
图 1 淮河流域概况 Fig. 1 The profile of Huaihe River Basin |
2015—2017年6—8月逐小时雨量观测数据来源于全国综合气象信息共享平台(China Integrated Meteorological Information Service System, CIMISS)。观测站点包括:淮河流域172个国家地面气象观测站;河南1278个区域雨量站;安徽733个区域雨量站,山东611个区域雨量站,江苏758个区域雨量站;湖北8个区域雨量站。王家坝水文站流量的观测数据来自安徽省水利厅水文局(www.ahsl.gov.cn)。
2.2 数值模式降水预报产品2015—2017年淮河汛期6—8月的全球模式ECMWF和JMA降水预报产品是通过中国气象局气象数据卫星广播系统(The Satellite Broadcasting System of China Meteorological Administration,CMACast)收集获取。同时段的INCA和WRF等中尺度模式降水预报产品则为安徽省气象台实时业务化运行且保存的。模式详细介绍见表 1。
|
|
表 1 各数值模式概况 Table 1 Basic information of four numerical weather predictions |
淮河流域数字高程模型(DEM)来源于美国地质调查局(US Geographic Survey, USGS,https://www.usgs.gov/),分辨率为15″×15″。利用ArcGIS软件对DEM进行填洼处理,并对填洼后的DEM按照研究区域进行切割。利用水文分析功能,根据DEM生成流向(FDR)及汇流累积量(FAC),最终由汇流累积量设置阈值生成河网(图 2)。

|
图 2 王家坝以上淮河上游的流向(a)、汇流累积量(b)及河网(c) Fig. 2 Flow direction (a), flow accumulation (b) and river network (c) in upstream of Huaihe River Basin |
面雨量是指整个流域面上的平均降水量。本文利用泰森多边形法计算实况面雨量(方慈安等,2003)。其原理是将小流域内各相邻雨量站相连,绘制各连线的垂直平分线,将小流域分成若干个单元面积,每个单元面积内只包含1个测站。首先计算流域各站在一定时段内的累积降雨量,然后根据每个雨量站所占流域面积权重,采用加权法对小流域各雨量站的累积降水量进行叠加求和。面雨量计算公式为:
| $ P=\sum\limits_{i=1}^{n} \omega_{i} P_{i} $ |
式中,ωi为小流域内各雨量站权重,n为流域内雨量站个数,均无量纲;Pi为流域内各雨量站的时段降水量(单位:mm)。
数值模式降水预报的面雨量则采用网格算术平均法进行估算,即计算子流域范围内网格点上的雨量平均值。对于JMA、EC等较低分辨率的数值模式格点产品,首先对其进行空间插值,使其网格距达到0.1°×0.1°,再采用网格算术平均法估算流域面雨量预报。
2.5 面雨量等级标准本文中需评估多时间尺度(1、3、6、12、24 h)的面雨量预报效果,但我国《江河面雨量等级划分标准》(GB/T 20486—2017)(中华人民共和国国家质量监督检验检疫总局和中国国家标准化管理委员会,2017)只有12和24 h的面雨量等级标准,因此本文结合《安徽省短时临近降水强度地方标准》(DB/T 1592—2012)(安徽省质量技术监督局,2017),规定当1、3、6、12和24 h面雨量分别达到或超过5、10、15、20、30 mm时,该时间尺度的面雨量达到暴雨量级。
2.6 预报质量评估方法模式降水预报质量评估采用TS评分、漏估率(PO)、空估率(FAR)等评价指标。TS,PO及FAR分别按下式计算:
| $ T S_{k}=\frac{N A_{k}}{N A_{k}+N B_{k}+N C_{k}} \times 100 \% $ | (1) |
| $ P O_{k}=\frac{N C_{k}}{N A_{k}+N C_{k}} \times 100 \% $ | (2) |
| $ F A R_{k}=\frac{N B_{k}}{N A_{k}+N B_{k}} \times 100 \% $ | (3) |
式中,k为预报等级,NAk为降水预报正确次数,NBk为空报次数,NCk为漏报次数。
选取效率系数(nash-sutcliffe efficiency,NSE)(Nash and Sutcliffe, 1970)及相对误差(Bias)相关系数(CC)作为评价水文模拟和预报效果的指标。计算公式如下:
| $ N S E=1-\frac{\sum\limits_{i=1}^{n}\left(R_{\mathrm{obs}, i}-R_{\mathrm{sim}, i}\right)^{2}}{\sum\limits_{i=1}^{n}\left(R_{\mathrm{obs}, i}-\overline{R}_{\mathrm{obs}}\right)^{2}} $ | (4) |
| $ CC = \frac{{\sum\limits_{i = 1}^n {\left({{R_{{\rm{obs}}, i}} - {{\overline R }_{{\rm{obs}}}}} \right)\left({{R_{{\rm{sim}}, i}} - {{\overline R }_{{\rm{sim}}}}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left({{R_{{\rm{obs}}, i}} - {{\bar R}_{{\rm{obs}}}}} \right)}^2}\sum\limits_{i = 1}^n {{{\left({{R_{{\rm{sim}}, i}} - {{\overline R }_{{\rm{sim}}}}} \right)}^2}} } } }} $ | (5) |
| $ Bias = \left[ {\frac{{\sum\limits_{i = 1}^n {{R_{{\rm{sim}}, i}}} - \sum\limits_{i = 1}^n {} {R_{{\rm{obs}}, i}}}}{{\sum\limits_{i = 1}^n {} {R_{{\rm{obs}}, i}}}}} \right] \times 100 $ | (6) |
式中:Robs,i、Rsim,i分别为径流量观测值和模拟值;
CREST模型是由俄克拉荷马大学和NASA的SERVIR项目组(www.servir.net)在2011年共同研发的分布式水文模型,之后不断被改进和完善,于2014年推出最新版本2.1版。其基本架构如图 3所示,输入数据主要包括初始条件、潜在蒸散发、降水、地理信息、模型参数等。CREST模型的基本原理为经过冠层截留后的降水落到地面,根据变化下渗曲线,一部分渗透到土壤里,形成壤中流,另一部分则在地表产流。在冠层截留、下渗土壤和地表产流的同时,均伴随着蒸散发过程。壤中流和地表径流分别沿着水力梯度方向汇入河道,再由河道汇集到流域出水口。由于CREST模式是以网格为最小计算单元来计算产流、汇流,网格大小可由用户根据地理信息的精度自定义,因此CREST模型不仅适用于全球尺度、大尺度的水文模拟,也可用于模拟中小流域的水文过程。

|
图 3 CREST水文模型的基本构架 Fig. 3 Programming framework of CREST model |
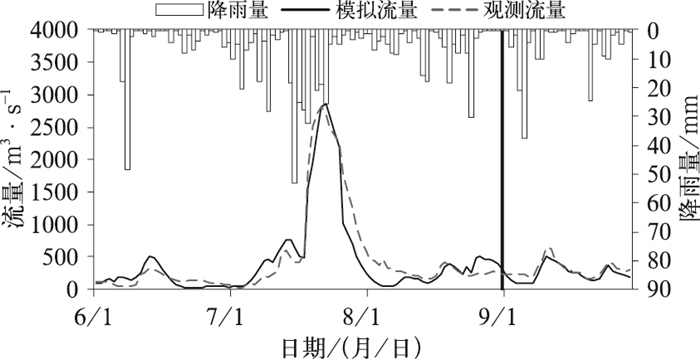
使用2010年5—8月淮河流域区域自动站24 h(08时至次日08时)累积降水资料驱动CREST模型,利用王家坝的逐日观测流量(观测时刻为08时),以NSE为目标函数,采用SCE-UA方法(Duan et al, 1994)对CREST模型进行率定(其中5月数据用于模型预热),率定后的参数见表 2。利用2010年9月的相关数据进行模型的验证。结果如图 4所示,在率定期王家坝水文控制站的NSE高达0.91,模拟流量和观测流量的相关系数为0.95,相对误差为6.3%,CREST表现优异,可以较好地模拟王家坝的流量变化趋势。验证期模型的模拟效果要差于率定期,NSE降低到0.49,相关系数为0.85,通过0.01的显著性水平检验。相对误差比率定期明显增大,为20.1%,但仍小于25%的阈值。总体来说,CREST模拟结果可以较好地描述观测值,模型适用于淮河流域上游地区。
|
|
表 2 率定后的参数值 Table 2 Parameter value after calibration at Wangjiaba Station |
|
图 4 2010年6—9月率定期和验证期模拟流量和实测流量的对比 Fig. 4 Observed and simulated discharge in the calibration and validation period at Wangjiaba Station from June to September 2010 |
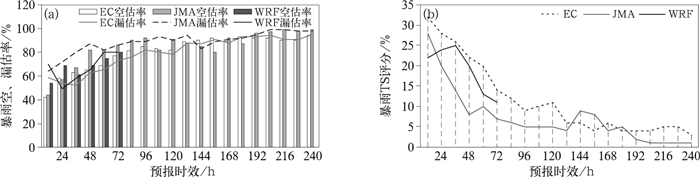
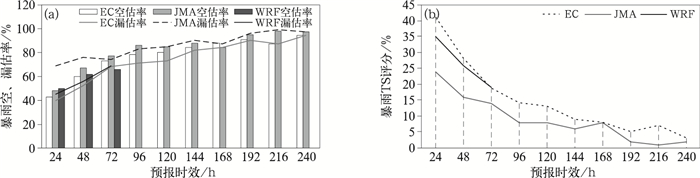
图 5表明在0~72 h预报时效内,EC、WRF和JMA三个模式的暴雨预报TS评分都随着预报时效的增加迅速降低。相比之下,EC具有最佳的预报性能,特别是在24 h预报时效,优势最为明显,对暴雨的预报TS评分可达41%,分别比WRF和JMA高6%和17%。随着预报时效的增加,WRF和EC的差距逐渐缩小,72 h时WRF的TS评分开始略比EC高2%。相比之下,在0~72 h,JMA的TS评分远低于前两个模式。当预报时效为96~240 h,EC和JMA两个模式的TS评分随着预报时效的增加缓慢降低。EC的预报质量要明显优于JMA,TS评分一般高出1%~6%不等。
|
图 5 24 h时间尺度暴雨预报的空、漏估率(a)和TS评分(b) Fig. 5 False alarm rate and missing forecast rate (a) and TS score (b) of 24 h rainstorm |
在24 h预报时效内,EC的空、漏估率分别为43%和40%,WRF较EC略偏高,但都处于相对较低的水平。JMA的漏估率高达69%,说明预报面雨量较实况严重偏小。随着预报时效的增加,三个模式的空、漏估率也快速增加。到了72 h预报时效,EC和WRF的漏估率超过60%,在168 h时EC的漏估率超过80%,几乎会漏报绝大部分的暴雨。
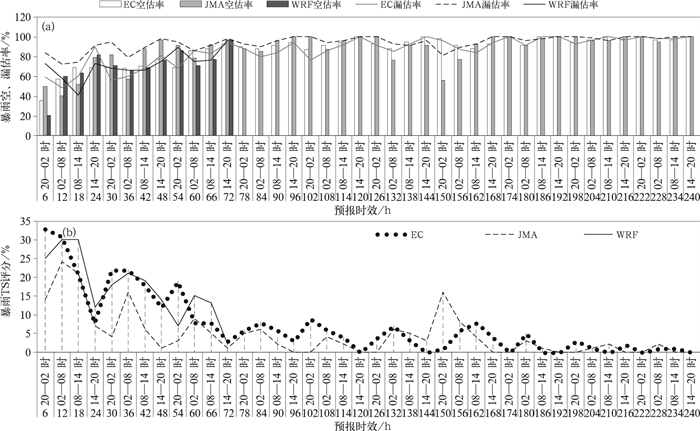
3.2 12 h时间尺度暴雨的预报评估对于12 h时间尺度达到暴雨的面雨量,在前72 h内EC仍保持最好的预报性能,WRF次之,JMA最差,TS评分比和前两个模式比显著偏低,在36~48 h预报时效,甚至比EC偏低了14%之多。在84~240 h预报时效内,EC对暴雨的预报能力整体来说仍强于JMA,但在132~180 h时效时内,JMA的TS评分时而反超EC。
EC的空、漏估率最低,尤其是0~36 h漏估率保持在50%~59%。WRF除了前12 h漏估率异常偏高外,在24~48 h和EC水平相当,但48 h后空、漏估率都高于EC。JMA的漏估率仍是三个模式中最高, 尤其是前72 h, 和其他两个模式差距最大,比EC高10%以上,最大相差28%。值得注意的是,对于12 h预报时效的暴雨预报,三个模式的漏估率普遍高于空估率,其他时效的预报则空、漏估率相当(图 6)。
3.3 6 h时间尺度暴雨的预报评估6 h时间尺度的暴雨预报质量表现出明显的日变化特征,整体来说,三个模式对于凌晨(02—08时)的暴雨预报效果最好,但对于午后到傍晚(14—20时)的暴雨预报效果最差,由于日变化导致的TS评分差距在前72 h表现最为显著,差距最高达23%。淮河流域夏季的这个时间段的暴雨一般为对流性暴雨,可见三个模式对中小尺度的暴雨预报能力有待提高。在前72 h预报时效内,WRF和EC的预报性能相差不大,JMA则是三个模式中预报性能最差的。对于78~240 h预报时效的暴雨预报,EC虽比JMA预报效果好,但两者的TS评分均低于10%,对暴雨均不具备预报能力(图 7)。
值得注意的是,三个模式在前0~6 h的漏估率都远超过空估率,且明显高于6~18 h预报时效的漏估率。在6~18 h预报时效内,EC易对暴雨空估,之后则空、漏估率相当,另外,EC对早晨时段的暴雨易空估。WRF和EC相似,在6~24 h预报时效内易对暴雨空估,之后则空、漏估率相当。JMA则在0~36 h预报时效内都以漏估为主,之后空、漏估率相当(图 7)。
3.4 3 h时间尺度暴雨的预报评估3 h时间尺度暴雨预报性能随预报时效的变化趋势和6 h时间尺度相似,也存在明显的日变化特征,但三个模式的预报性能峰值和谷值所在的时间段略有差别(图 8)。在前24 h, EC和WRF的趋势相似,均是在上半夜(23—02时)、凌晨到上午(05—11时)暴雨预报质量最高,而在午后到傍晚(14—20时)预报质量最低。而在27~72 h预报时效内,EC对夜里的暴雨预报能力强,白天的暴雨预报能力相对较弱,WRF则正好呈相反的趋势,对于发生在午后到傍晚的暴雨,WRF的TS评分要明显高于EC,可见WRF作为中尺度模式,对对流性暴雨的预报能力要强于全球尺度模式。JMA的预报性能则在上半夜(23—02时)的时候最低,到上午(08—11时)达到最高(图 8)。
三个模式在前12 h漏估率都远高于空估率,尤其是临近的0~3 h,三个模式的漏估率都在80%左右,因此在临近预报中,三个模式对暴雨的预报都不具备参考价值。JMA对于3 h时间尺度的暴雨几乎没有预报能力,所有预报时效内漏估率为79%~100%(图 8)。
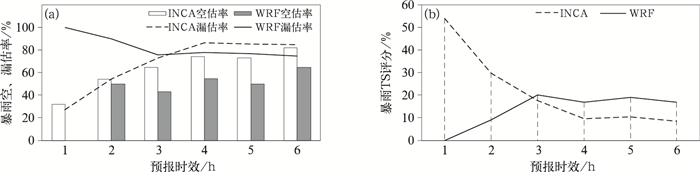
3.5 1 h时间尺度暴雨的预报评估由于EC和JMA等全球模式没有1 h时间尺度的预报产品,因此仅评估WRF和INCA的暴雨预报性能。由图 9可见,在1 h预报时效,WRF的暴雨TS评分为0,漏估率100%,对暴雨完全没有预报能力,随着预报时效的增加,WRF对暴雨的预报能力开始增强,2 h预报时效时TS为9%,漏估率减少到90%;3 h的TS快速增加到20%,漏估率为76%;在之后的4~6 h预报时效中,WRF的TS一直维持在20%左右,漏估率则维持在75%附近。WRF的空估率要明显低于漏估率,除了1 h预报时效空估率为0,其他时效的空估率在40%~65%。
和WRF相比,INCA表现出在临近预报中的绝对优势,尤其是1 h预报时效的暴雨预报,TS评分为54%,空、漏估率分别为32%和29%;2 h预报时效的暴雨预报质量快速降低,TS为30%,空、漏估率也上升到50%左右;从第3 h开始INCA的暴雨预报能力开始低于WRF;4~6 h暴雨预报TS仅在10%左右,空、漏估率为70%~90%。
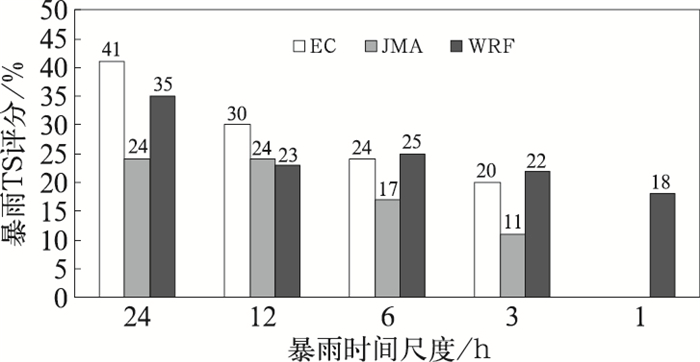
3.6 各时间尺度暴雨预报性能的对比为对比分析时间尺度对暴雨预报性能的影响,选取EC、JMA、WRF等3 h累积降水、6 h累积降水、12 h累积降水、24 h累积降水等预报产品的在0~24 h预报时间段内的平均暴雨TS评分以及命中率,同时计算WRF第5~6 h平均暴雨TS评分以及命中率。由图 10可见,在EC、JMA和WRF三个模式中,JMA对各个时间尺度的暴雨的预报能力都是最差的,EC对24 h时间尺度的暴雨预报性能最优,TS为41%,WRF的预报效果略差。随着暴雨的历时越来越短,两个模式的预报性能逐渐减低,但EC暴雨预报性能降低的速度较WRF更快,在对3 h时间尺度暴雨的预报中,WRF的预报能力开始超越EC。在对1 h时间尺度暴雨的预报中,WRF的TS评分降低到18%。
|
图 10 各时间尺度暴雨预报性能的对比 Fig. 10 Comparison of forecasting performances for different time-scale rainstorms |
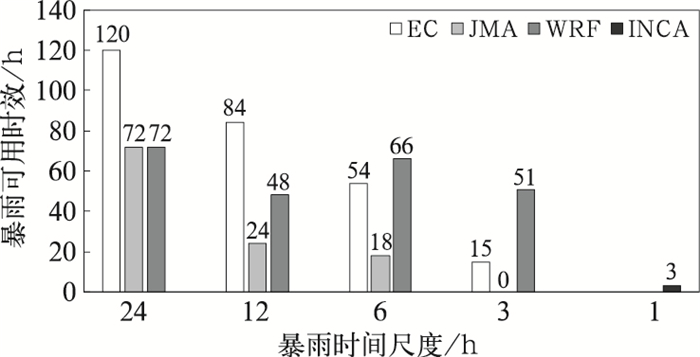
由于目前对于暴雨预报的可用时效没有统一的标准,本文以漏估率为80%作为暴雨预报可用与否的阈值,当连续有两个时次漏估率超过80%,则认为暴雨预报的可用时效为漏报率首次超过阈值之前的时次。以此标准统计各模式在各个时间尺度下暴雨的可用时效。由图 11可知,EC对24 h时间尺度暴雨预报的可用时效最长,为120 h,随着暴雨时间的缩短,EC的可用时效迅速下降为84 h(12 h暴雨)、54 h(6 h暴雨)、15 h(3 h暴雨)。JMA的下降趋势和EC相同,但可用时效较EC大幅缩短,分别为72 h(24 h暴雨)、24 h(12 h暴雨)、18 h(6 h暴雨),JMA对于3 h时间尺度暴雨没有预报能力。WRF对暴雨预报的可用时效和前两个模式相比有所区别,对于24 h暴雨可用时效为72 h(WRF最长时效为72 h);当预报12 h时间尺度的暴雨时,可用时效减少到48 h;但当预报6 h时间尺度暴雨时,可用时效又增加至66 h,比EC的可用时效多12 h;当对3 h时间尺度的暴雨进行预报时,WRF的可用时效为51 h,比EC明显偏长。INCA对1 h时间尺度暴雨的可用时效为3 h。
|
图 11 各模式对各个时间尺度暴雨预报的可用时效 Fig. 11 The lead time of usable forecasts for different time-scale rainstorms from four NWPs |
综合以上评估结果,EC模式24 h累积的降水预报产品对暴雨的预报可用时效最长,且和CREST水文模型率定时使用的降水量有着相同的时间步长,因此将其作为CREST的驱动条件,建立王家坝以上淮河上游气象水文耦合洪水预报模型。该模型从2016年6月1日实时运行,2016年6—8月、2017年5—8月各预见期的流量预报和实测流量的变化趋势对比见图 12(由于实时运行时存在输入数据缺失或程序故障现象,导致某些日期无水文预报结果,因此各图横坐标的日期并不完全一致)。由图 12可知预报时效少于108 h时,流量预报基本可以较为准确地捕捉洪峰的出现时间,但对洪峰流量普遍存在低估,随着预见期的缩短,对洪峰流量的预报准确率增加。定量检验结果表明,从12~108 h时效,效率系数NSE分别为0.64,0.60,0.55,0.48,0.36,超过0.36的阈值;相关系数分别为0.81,0.80,0.78,0.71和0.64,表明该预报系统对未来4 d的流量具有一定的预报能力,可以给预报员提供有价值的参考,到132 h,效率系数降为0.29,相关系数为0.60,表明对于未来第5天虽然流量模拟能力降低,但模拟流量和实测流量仍具有较好的相关性,仍具有一定的参考价值。而156 h后效率系数则低于0,相关系数则为0.37~0.2,表明该预报系统对于6天以后的流量预报能力较弱。
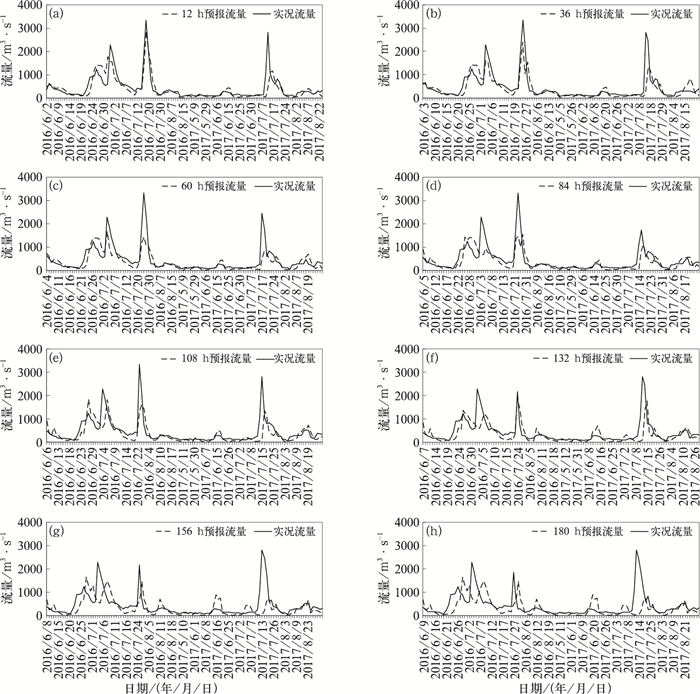
|
图 12 各预报时效的预报流量及实况流量对比图 (a)12 h,(b)36 h,(c)60 h,(d)84 h,(e)108 h,(f)132 h,(g)156 h,(h)180 h Fig. 12 The observed and simulated discharge with different lead times (a) 12 h, (b) 36 h, (c) 60 h, (d) 84 h, (e) 108 h, (f) 132 h, (g) 156 h, (h) 180 h |
选取王家坝一次超警洪水过程对洪水的可预报性进行更加细致的探讨。2016年7月19日08时至20日08时淮河流域出现明显降水过程,最强降水时段位于19日23时至20日15时,王家坝水位自21日起迅速上涨,22日出现洪峰流量3340 m3·s-1,水位达27.75 m,超警戒水位0.25 m,王家坝开闸向蒙洼蓄洪区泄洪。17日开始,气象水文耦合洪水预报系统一直预报在22日有一次明显的涨水过程,且流量预报不断更新,越来越接近实测流量,在20日起报的预报结果中流量预测值为2380 m3·s-1。如果不考虑数值预报的耦合,仅使用降雨量实况驱动模型,则在20日前流量的预报均不能预测到涨水过程。仅在20日起报的预报中,预计22和23日的流量均超过1400 m3·s-1(图 13)。虽然此次洪峰过程,气象水文耦合系统对洪峰流量存在低估,但在洪峰5天前对水势起涨时间把握较好,可以给防灾减灾赢得宝贵的准备时间。
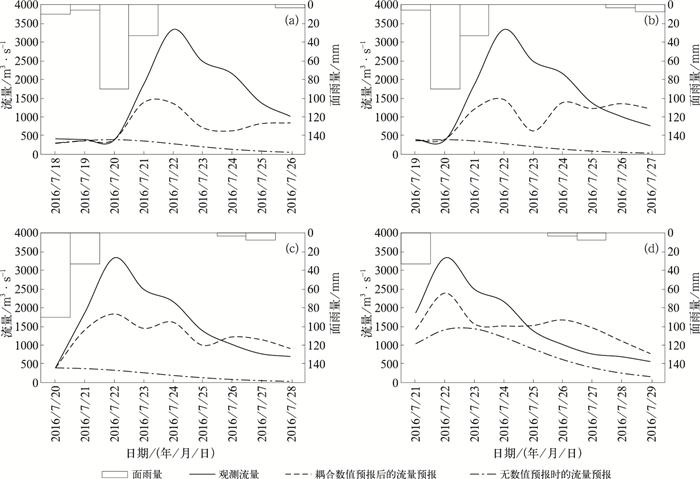
|
图 13 2016年7月17日(a)、18日(b)、19日(c)和20日(d)起报的流量预报及未耦合数值预报的流量预报对比 Fig. 13 Comparison of discharge forecasts driven by NWP and observed precipitation at different forecast time on (a) 17 July, (b) 18 July, (c) 19 July and (d) 20 July 2016 |
(1) 在EC、JMA和WRF三个模式中,对于24 h时间尺度的暴雨,EC预报性能最优,TS为41%,WRF的预报性能略差。随着暴雨的历时越来越短,两个模式的预报性能逐渐减低,但EC暴雨预报性能降低的速度较WRF更快,在对6 h时间尺度暴雨的预报中,WRF的预报能力开始超越EC;当暴雨的时间尺度为3 h时,WRF的优势更为突出。JMA对各个时间尺度的暴雨的预报能力均最差,参考价值较低。
(2) EC在0~6 h预报时效内存在漏报率异常偏高的现象,WRF则在前12 h就存在这种现象,且更加明显。特别是对于0~3 h时效内暴雨的预报,EC和WRF漏报率超过80%。造成这种现象的原因可能是模式在较短时效内仍处于预热阶段。JMA在临近时效内预报质量异常偏低的现象并不明显,但由于JMA暴雨预报质量较差,因此在临近预报中,三个模式的暴雨预报都不具备参考价值。
(3) INCA表现出在临近预报中的绝对优势,尤其是1 h预报时效的暴雨预报,TS评分为54%。随着预报时效的增加,INCA的预报性能迅速下降。而WRF则在1 h预报时效对暴雨100%漏报,随着预报时效的增加,WRF在3 h时预报时效时和INCA预报能力相当,而在4 h时超越INCA。
(4) EC、JMA和WRF对6 h时间尺度和3 h时间尺度的暴雨预报性能存在明显的日变化特征,总体来看,三个模式对于午后到傍晚(14—20时)的暴雨预报质量最差,由于日变化导致的TS评分差距最高达23%。淮河流域夏季午后到傍晚的暴雨多为对流性质,可见三个模式对中小尺度的暴雨预报能力有待提高。当暴雨的时间尺度为3 h时,WRF对对流性暴雨预报能力明显高于全球模式EC、JMA。
(5) EC对24 h时间尺度暴雨预报的可用时效长达120 h,随着暴雨时间尺度的减小可用时效迅速缩短,JMA和EC有相同的趋势,但可用时效要远短于EC。当暴雨时间尺度为6 h,WRF的可用时效开始长于EC,当暴雨时间尺度为3 h,WRF的可用时效为51 h,远远长于EC的15 h。INCA对暴雨预报的可用时效为3 h。
(6) 以EC的24 h累积降水预报产品驱动CREST模型,得到洪水预报的可用时效为108 h,在该时效内,流量预报基本可以较为准确地捕捉洪峰的出现时间,但对洪峰流量普遍存在低估。
安徽省质量技术监督局, 2012.短时临近降雨强度等级划分: DB34/T 1592—2012[S].合肥: 安徽省地方标准. Anhui Provincial Bureau of Quality and Technical Supervision, 2012.Grade classification of nowcasting rainfall intensity: DB34/T 1592-2012[S].Hefei: Anhui Provincial Local Standards(in Chinese). |
包红军, 王莉莉, 沈学顺, 等, 2016. 气象水文耦合的洪水预报研究进展[J]. 气象, 42(9): 1045-1057. Bao H J, Wang L L, Shen X S, et al, 2016. A review:advances of flood forecasting of hydro-meteorological forecast technology[J]. Meteor Mon, 42(9): 1045-1057 (in Chinese). |
包红军, 张珂, 魏丽, 等, 2017. 淮河流域2016年汛期洪水预报试验[J]. 气象, 43(7): 831-844. Bao H J, Zhang K, Wei L, et al, 2017. Test on flood forecasts for Huaihe River in the 2016 flood season[J]. Meteor Mon, 43(7): 831-844 (in Chinese). |
包红军, 赵琳娜, 2012. 基于集合预报的淮河流域洪水预报研究[J]. 水利学报, 43(2): 216-224. Bao H J, Zhao L N, 2012. Flood forecast of Huaihe River based on TIGGE ensemble predictions[J]. J Hydraulic Eng, 43(2): 216-224 (in Chinese). |
毕宝贵, 矫梅燕, 李泽椿, 2004. 2003年淮河流域洪涝暴雨的气象水文特征分析[J]. 南京气象学院学报, 27(5): 577-586. Bi B G, Jiao M Y, Li Z C, 2004. Contrast analysis of meteorological and hydrological features of extremely heavy rainfall causing severe floods in Huaihe River Valley[J]. J Nanjing Inst Meteor, 27(5): 577-586 (in Chinese). |
董全, 金荣花, 代刊, 等, 2016. ECMWF集合预报和确定性预报对淮河流域暴雨预报的对比分析[J]. 气象, 42(9): 1146-1153. Dong Q, Jin R H, Dai K, et al, 2016. Comparison between ECMWF ensemble and deterministic forecast for heavy rainfall in the Huaihe River Basin of China[J]. Meteor Mon, 42(9): 1146-1153 (in Chinese). |
方慈安, 潘志祥, 叶成志, 等, 2003. 几种流域面雨量计算方法的比较[J]. 气象, 29(7): 23-26, 42. Fang C A, Pan Z X, Ye C Z, et al, 2003. Comparison of calculation of methods river valley area rainfall[J]. Meteor Mon, 29(7): 23-26, 42 (in Chinese). |
甘衍军, 徐晶, 赵平, 等, 2017. 暴雨致洪预报系统及其评估[J]. 应用气象学报, 28(4): 385-398. Gan Y J, Xu J, Zhao P, et al, 2017. Introduction and evaluation of a rainstorm-caused flood forecasting system[J]. J Appl Meteor Sci, 28(4): 385-398 (in Chinese). |
刘静, 叶金印, 张晓红, 等, 2014. 淮河流域汛期面雨量多模式预报检验评估[J]. 暴雨灾害, 33(1): 58-64. Liu J, Ye J Y, Zhang X H, et al, 2014. The performance evaluation of the multi-model forecasting of areal rainfall for Huaihe River Basin during flood season[J]. Torr Rain Dis, 33(1): 58-64 (in Chinese). |
卢燕宇, 田红, 2015. 基于HBV模型的淮河流域洪水致灾临界雨量研究[J]. 气象, 41(6): 755-760. Lu Y Y, Tian H, 2015. Mechanism oriented approach for estimating critical rainfall of flood disaster:a case study based on HBV model[J]. Meteor Mon, 41(6): 755-760 (in Chinese). |
王会军, 张颖, 郎咸梅, 2010. 论短期气候预测的对象问题[J]. 气候与环境研究, 15(3): 225-228. Wang H J, Zhang Y, Lang X M, 2010. On the predictand of short-term climate prediction[J]. Climatic Environ Res, 15(3): 225-228 (in Chinese). |
叶金印, 张锦堂, 黄勇, 等, 2017. 大别山库区降水预报性能评估及应用对策[J]. 湖泊科学, 29(6): 1528-1537. Ye J Y, Zhang J T, Huang Y, et al, 2017. Evaluation of precipitation forecasts for Dabie Mountain area and application countermeasures for the reservoirs regulation[J]. J Lake Sci, 29(6): 1528-1537 (in Chinese). |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2017.江河流域面雨量等级: GB/T 20486-2017[S].北京: 中国标准出版社. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Management Committee, 2017.Grade of valley area precipitation: GB/T 20486-2017[S].Beijing: Standards Press of China(in Chinese). |
朱占云, 陈光宇, 姜瑜君, 等, 2016. 浙江省六大水库流域面雨量模式预报效果检验[J]. 气象与环境学报, 32(3): 28-33. Zhu Z Y, Chen G Y, Jiang Y J, et al, 2016. Evaluation of the prediction by area rainfall forecast model OCF for six big reservoir basins in Zhejiang Province[J]. J Meteor Environ, 32(3): 28-33 (in Chinese). |
Duan Q Y, Sorooshian S, Gupta V K, 1994. Optimal use of the SCE-UA global optimization method for calibrating watershed models[J]. J Hydrol, 158(3-4): 265-284. DOI:10.1016/0022-1694(94)90057-4
|
Haiden T, Kann A, Wittmann C, et al, 2011. The integrated Nowcasting Through Comprehensive Analysis (INCA) System and its validation over the Eastern Alpine Region[J]. Wea Forecasting, 26(4): 166-183.
|
Nash J E, Sutcliffe J V, 1970. River flow forecasting through conceptual models Part Ⅰ-a discussion of principles[J]. J Hydrol, 10(3): 282-290. DOI:10.1016/0022-1694(70)90255-6
|
Todini E, 2007. Hydrological catchment modelling:past, present and future[J]. Hydrol Earth Syst Sci, 11(1): 468-482. DOI:10.5194/hess-11-468-2007
|
Wang J H, Hong Y, Li L, et al, 2011. The coupled routing and excess storage (CREST) distributed hydrological model[J]. Hydrol Sci J, 56(1): 84-98.
|
Wang Y, Meirold-Mautner I, Kann A, et al, 2017. Integrating nowcas -ting with crisis management and risk prevention in a transnational and interdisciplinary framework[J]. Meteor Z, 26(5): 459-473. DOI:10.1127/metz/2017/0843
|
Xue X W, Hong Y, Zhang K, 2015.CREST-Coupled Routing and Excess Storage User Manual, Version 2.1[M].Norman: University of Oklahoma.
|
 2019, Vol. 45
2019, Vol. 45