2. 南京大学大气科学学院中尺度灾害性天气教育部重点实验室,南京 210023
2. Key Laboratory of Mesoscale Severe Weather/Ministry of Education and School of Atmospheric Sciences, Nanjing University, Nanjing 210023
集合预报与确定性预报相比具有额外的优势,它可以通过概率预报来反映初始条件及模式本身造成的不确定性。随着计算能力和中尺度数值模式的提升,中尺度预报模式的分辨率显著提高,已经有可能分辨积云对流尺度的系统,而不需要传统的积云对流参数化过程。考虑到强对流天气时空尺度小且伴随多尺度系统复杂的非线性相互作用,其不确定性更加突出。因此,将高分辨率模式与集合预报相结合,可以充分发挥两者在强对流天气预报方面的优势,对流尺度集合预报已成为国内外研究的热点(Roebber et al, 2004; Vié et al, 2011; Fang et al, 2011; Clark et al, 2012;谭燕和陈德辉, 2008;庄潇然等, 2016; 陈涛等, 2017),通常将3~5 km水平网格距的预报称为对流许可尺度,1~2 km水平分辨率的预报称为风暴尺度,而把1 km及更高分辨率(几百米)预报称为对流可分辨尺度。
2014年上海南汇WSR-88D雷达完成了双偏振升级改造(尹春光等, 2015),双偏振雷达使用水平和垂直极化波束观测大气,比反射率因子包含更多的粒子尺度分布信息(Kumjian and Ryzhkov, 2008)。例如,差分反射率(目标物对水平和垂直偏振波平行分量散射能量的差异)可用来判断采样体积内降水粒子的形状,其值取决于降水粒子的水平和垂直轴比。大雨滴在下落过程中受到自身重力、周围空气压力等作用发生形变,呈近似椭圆型,水平和垂直轴差别较大,因此差分反射率值较大;而干冰雹在下落过程中由于翻滚,呈近似球形,水平和垂直轴接近,差分反射率值较小(Bringi and Chandrasekar, 2001)。
2011—2013年美国WSR-88D的S波段雷达业务网升级为双偏振雷达,国外已有很多研究通过模式双偏振雷达预报量与观测的对比,来评估真实个例中利用数据同化诊断或模式预报的微物理状态(Jung et al, 2012; Li and Mecikalski, 2012; Dawson II et al, 2014; Putnam et al, 2014; Posselt et al, 2015)。Putnam et al(2017a)在灾害性天气春季试验中通过采用风暴尺度(2 km)集合预报系统,研究了不同微物理方案在模拟双偏振雷达特征能力方面的差异,但并未研究其在集合概率预报方面的表现。Putnam et al(2017b)则使用集合卡尔曼滤波初始化和不同微物理参数化方案对一次中尺度对流系统进行了集合概率预报,定性和定量评估了模拟的双偏振变量,研究表明双参数微物理方案的结果与实况更为接近,能更好地区分层云和对流区。然而,国内双偏振雷达(特别是S波段)并未普及,在这方面的研究仍较少。相比其他强对流灾害(如龙卷、雷暴大风和短时强降水),使用集合预报直接预报冰雹的研究也相对较少,其中一部分原因是由于缺乏高质量高分辨率的冰雹观测数据,而双偏振雷达观测在冰雹的识别上具有显著的优势。Snook et al(2016)利用集合预报提供了冰雹预报的不确定信息,指出在经过同化后的高分辨率(500 m)对流可分辨尺度集合预报能够很好地对冰雹进行预测,同时双偏振雷达观测可以作为冰雹检验的补充信息。
对流尺度数值预报研究显示,其预报效果可以通过改善初始条件和模式物理参数化得以提高。ARPS(Advanced Regional Prediction)的资料分析系统(ARPS Data Analysis System,ADAS)使用观测资料和模式初始分析场,利用物理定律和经验关系构造网格尺度初始水物质场的云分析方法能够改善初始的水物质分布,同时结合传统的客观分析方法增加中小尺度信息,能够提高模式初始场质量,提升预报的准确性(Xue et al, 2003; Hu et al, 2006)。
本文利用全球集合预报系统(Global Ensemble Forecast System, GEFS)提供的大尺度扰动信息构造对流许可尺度集合预报,对模式输出的预报结果进行双偏振变量诊断,并与观测进行对比,研究改善初始水物质场,并增加小尺度信息对强对流天气特别是大粒子降水和冰雹预报的影响。本文根据初始条件的差异将对流许可尺度集合预报分为两组对比试验,一组完全采用大尺度GEFS场的扰动得到,另一组则通过ADAS系统调整初始水物质分布并增加了小尺度信息得到。以2015年4月28日发生在华东地区的一次伴随短时强降水和冰雹的强对流过程为例,结合上海南汇双偏振雷达基数据观测,定性和定量评估了两组试验对反射率因子、差分反射率及冰雹集合预报的结果,分析了通过初始资料客观分析改善水物质分布和增加小尺度信息对预报结果的影响。
1 试验设计及个例选取 1.1 集合预报系统设计本研究的集合预报基于WRF_ARW(Weather Research and Forecasting, Advanced Research WRF)模式建立。水平分辨率为3 km,属于对流许可尺度,垂直层数50层,水平格点数为621×499,采用的WRF版本是V3.9,模式覆盖范围如图 1所示。

|
图 1 模式区域、初始客观分析和云分析中使用的地面观测站点分布 (黑点:雷达站,蓝点:地面自动观测站,红点:国家级观测站,黑五角星:上海南汇双偏振雷达位置) Fig. 1 Model domain, the distribution of ground observations for data analysis (black dots: radar sites, blue dots: regional automatic weather station sites, red dots: nation-level surface station sites, pentagram: location of Shanghai Nanhui Dual-Polarization Radar) |
本文设计了两组集合预报系统,均由1个控制预报成员和14个扰动预报成员组成,采用1°分辨率的GEFS预报场作为模式初始驱动场和侧边界场,两组试验除初始场外,模式的设置及侧边界场均完全相同。其中一组集合预报试验作为控制试验,初始场采用WRF前处理系统(WRF Preprocessing System,WPS)直接得到(以下简称CTRL试验),而另一组则采用ADAS资料分析系统(以下简称ADAS试验),结合观测资料(地面观测站分布见图 1)对初始场进行调整,采用逐步订正法对常规资料(地面自动站及国家站)进行客观分析,并使用非常规观测(雷达反射率因子观测及FY-2E静止气象卫星的红外和可见光通道观测)资料进入复杂云分析系统,对初始场中的水物质量进行调整,从而使得模式的初始场更加接近真实的大气状态。
考虑到物理过程不确定性的重要性,也为使预报系统具有更好的集合离散度,本文对不同成员使用了不同的陆面模式、地表方案和行星边界层方案组合(表 1)。WRF目前版本的微物理方案包含单参数和双参数方案,其中双参数方案预报量包括粒子的质量浓度和数浓度,利用粒子数浓度的预报可以对双偏振雷达变量进行计算,从而实现对双偏振雷达变量的诊断预报。Milbrandt-Yau双参数(以下简称MY2)方案(Milbrandt and Yau, 2005)能够区分冰雹和霰,对其分别进行计算,因此本文所有集合成员的微物理参数化方案均使用MY2方案。
|
|
表 1 对流许可尺度集合预报系统各个成员的参数化配置 Table 1 Parameterization configuration for each member of the convection-allowing ensemble forecasts |
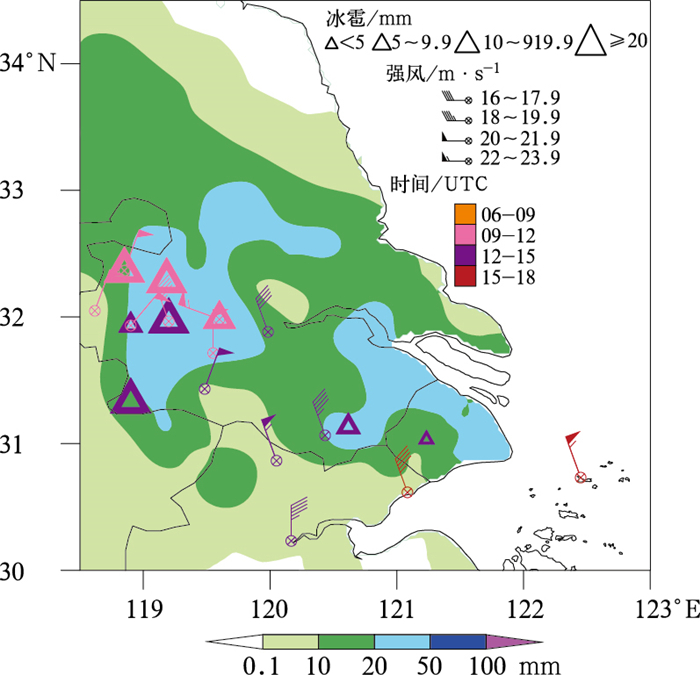
本研究选取2015年4月28日华东地区的一次强对流过程作为试验个例,此次过程具有影响范围大、强度强、持续时间长等特点(穆瑞琪等, 2015; 李佳等, 2017;吴海英等,2017)。28日00时(世界时,下同)的高低空天气形势分析显示,深厚的华北冷涡南落,冷涡后部偏北急流伴随干冷平流,叠置于低空的偏南暖湿平流之上,导致上下温差大,形成强的不稳定层结,在地面中尺度辐合区产生强对流天气(图略)。强对流回波从28日05时起,自山东南部向南移动发展,逐渐影响江苏、上海和浙江北部,过程中伴随出现了雷暴大风、短时强降水和冰雹等多种灾害性天气(图 2),此外,据相关报道,徐州、宿迁、淮安、盐城、南京、扬州、镇江、常州、无锡、苏州以及上海西南的局部地区也出现了冰雹(江苏省2015年4月气候影响评价,http://www.jsmb.gov.cn/art/2015/5/6/art_69_26898.html;吴海英等,2017)。
|
图 2 2015年4月28日00时至29日00时灾害性天气分布图 (三角形:产生降雹的站点,大小代表降雹直径,颜色代表发生降雹的时间;风向杆:产生大风的站点,颜色代表发生大风的时间;填色为24 h降水量) Fig. 2 Disaster distribution from 0000 UTC 28 to 0000 UTC 29 April 2015 (Triangles are stations with hail, the size represents hail diameter, color represents the time having hail; wind barbs are stations seeing strong winds and the color represents the time with strong wind; shaded area represents the 24 h rainfall amount) |
试验起报时间为00时,两组试验均预报18 h,由于12时起强对流回波开始影响长三角地区,进入上海南汇雷达观测范围之内,且在地面观测到了较大冰雹(图 2),因此本文主要针对12—14时的预报结果进行对比分析。
2 数据处理 2.1 雷达反射率因子及双偏振变量的诊断预报本文的模式后处理采用奥克拉荷马大学风暴分析与预测中心(Center for Analysis and Prediction of Storms, CAPS)研发的CAPS-PRS_V1.0(CAPS Polarimetric Radar data Simulator),它是一种用于具有显式微物理方案非静力天气预报模型的通用偏振雷达数据模拟器,支持5种WRF模式的微物理方案:新Thompson方案、MY2方案、Morrison双参方案、WDM6方案和NSSL双参方案。该模拟器基于雷达气象方程,利用WRF模式输出的粒子混合比和数浓度,构建粒子数浓度分布(PSD),结合粒子的密度和形状,通过散射截面加权对PSD积分得到水平偏振和垂直偏振的反射率因子,来计算双偏振雷达变量(Vivekanandan et al, 1991; Zhang et al, 2001; Jung et al, 2008; 2010)。WRF模式输出的预报数据通过CAPS-PRS计算得到雷达反射率因子及双偏振变量并插值到指定雷达(上海南汇雷达)的指定仰角,本文选择最低的0.5°仰角(12—14时观测中强对流回波所在位置的高度约2~4 km)是因为双偏振变量的特征在低仰角更为显著,且低仰角受到融化层的影响较小,便于与雷达观测(图 5a~5c和图 10a~10c)比较。
|
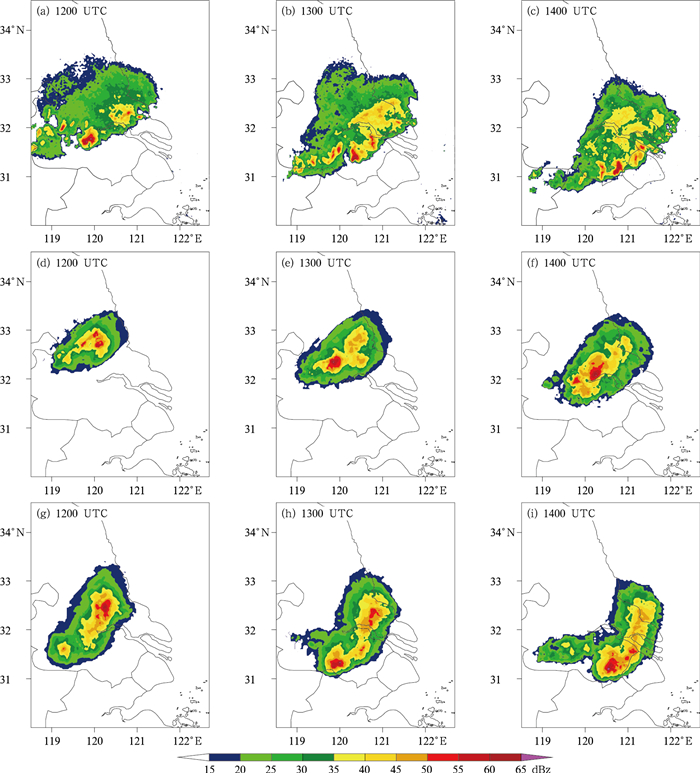
图 5 2015年4月28日12—14时上海南汇雷达0.5°仰角反射率因子分布 (a, b, c)观测,(d, e, f)CTRL试验的概率匹配集合平均(PMEM),(g, h, i)ADAS试验的概率匹配集合平均(PMEM) Fig. 5 Reflectivity (0.5° tilt) distribution of Shanghai Nanhui Radar in 1200-1400 UTC 28 April 2015 (a, b, c) observation, (d, e, f) probability matching ensemble mean of CTRL ensemble, (g, h, i) probability matching ensemble mean of ADAS ensemble |
|
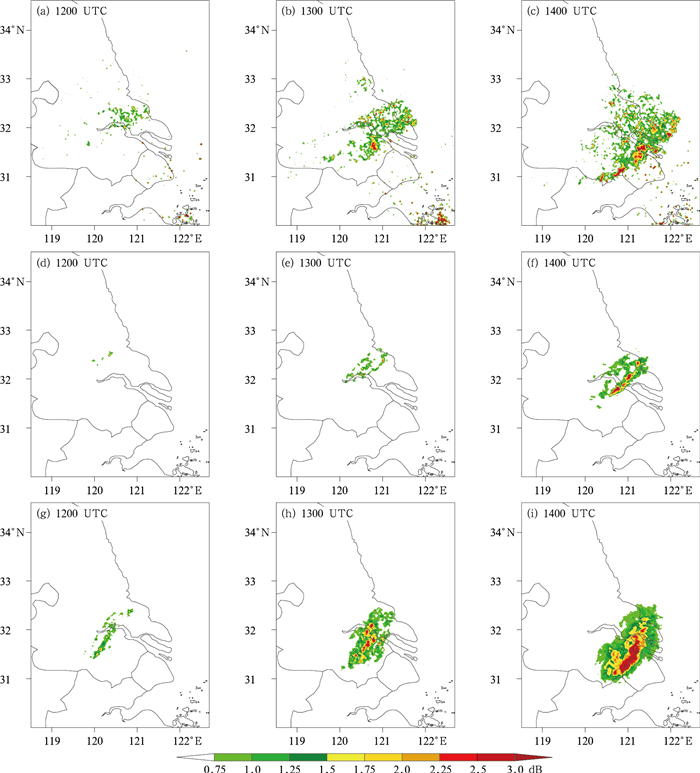
图 10 同图 5,但为差分反射率分布 Fig. 10 Same as Fig. 5, but for differential reflectivity (0.5° tilt) distribution |
为了对比CTRL试验和ADAS试验的初始场在不同尺度上的扰动分布特征,分别计算了两组试验中1个控制预报成员和14个成员初始场在不同尺度上的扰动总能量(EDT),计算式(李俊等, 2017)为:
| $ E_{D T}=\frac{1}{2} \sum\limits_{i, j, k}\left(u_{i, j, k}^{\prime 2}+v_{i, j, k}^{\prime 2}+\frac{c_{p}}{T_{r}} T_{i, j, k}^{\prime 2}\right) $ | (1) |
式中,u′,v′和T′分别为水平风场扰动及温度扰动,cp=1004 J·kg-1·K-1,Tr=270 K。尺度分解采用Haar二维小波分解方法,该方法将要素场分解为不同空间尺度的分量,对于n>1定义分解的格点区域为2n×2n,原始要素场可以在n+1个尺度上逐一进行分量的分解,且最终等于这些分量的总和;其中第i(1≤i≤n)个分量计算公式为原始要素场在2i-1×2i-1格点区域的平均场与原始要素场在2i×2i格点区域的平均场之差,第n+1个分量为整个区域的平均值,对于3 km格距的原始要素场,每个分量代表的是空间尺度为3×2i-1 km上的变化(Johnson et al, 2014),本文将分解后的3 km(3×20)作为小尺度部分的代表,96 km(3×25)作为中尺度部分的代表,768 km(3×28)作为大尺度部分的代表。
2.3 概率匹配集合平均(PMEM)概率匹配集合平均是将研究区域内集合平均和全部集合成员的变量值从大到小排列,然后将全部集合成员中变量值的概率密度函数值重新赋值给在集合平均中具有相同秩(顺序)的空间位置(Ebert, 2001)。本文中采用概率匹配集合平均而不采用常规的集合平均(算术平均),是由于反射率因子及双偏振变量在较小的范围内变化很快,当集合成员之间预报的对流回波存在微小的位置偏差时,简单的算术平均会导致预报变量值的低估及覆盖范围的偏大,而采用概率匹配集合平均则有利于减轻上述偏差。
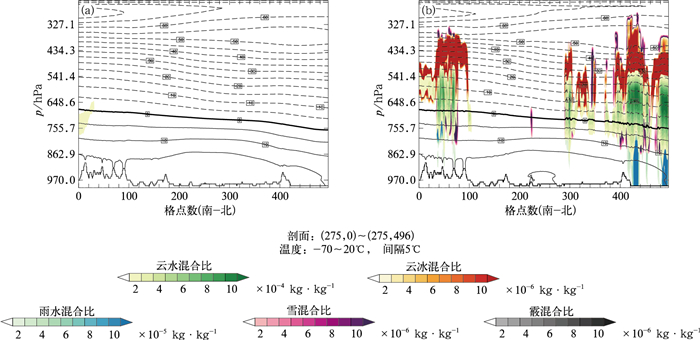
3 集合预报结果分析 3.1 初始场水物质和不同尺度扰动总能量分布对比图 3对比了模式初始时刻CTRL试验和ADAS试验中控制预报成员沿着117°E南北向的水物质(云水、云冰、雨水、雪和霰混合比)垂直分布,从图中可以看出,CTRL试验由于从全球集合预报系统GEFS数据插值得到,仅在最南侧的750 hPa附近有少量云水分布(图 3a),而经过ADAS试验的云分析系统后,由于综合考虑了雷达和卫星观测,在南北两侧750~400 hPa均有云水和云冰分布,雷达组合反射率图显示北侧已经有降水产生(图略),因此低层还存在雨水粒子(图 3b),由此可见,CTRL试验和ADAS试验初始水物质分布的差异显著。
|
图 3 控制预报成员初始时刻沿117°E(格点数275)的水物质南北向垂直分布 (a)CTRL试验,(b)ADAS试验 Fig. 3 Water substance distribution along 117°E (grid number 275) cross-section of the control member at the initial time (a) CTRL ensemble, (b) ADAS ensemble |
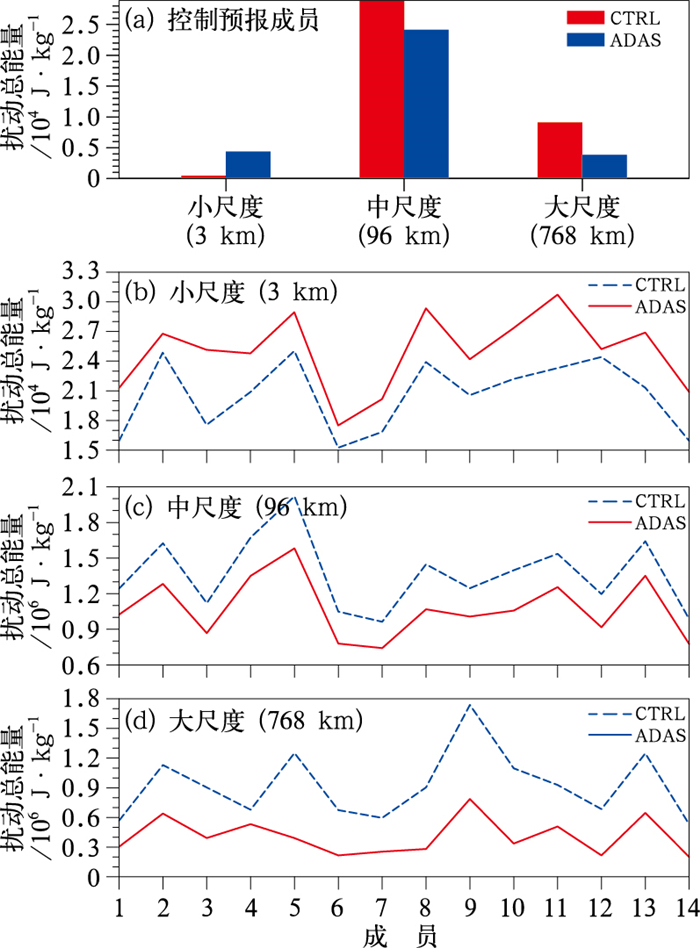
控制预报成员和14个成员的初始扰动总能量在不同尺度上的分布如图 4所示,在中尺度(96 km)上的扰动总能量大于小尺度(3 km)和大尺度(768 km),对比CTRL试验和ADAS试验可以发现,ADAS试验(图 4a中蓝色柱状,图 4b中实线)在小尺度的扰动总能量大于CTRL试验(图 4a中红色柱状,图 4b中虚线),而CTRL试验则在中尺度和大尺度的扰动总能量分布上大于ADAS试验。
|
图 4 初始时刻控制预报成员和14个集合成员在不同尺度上的扰动总能量分布 (a)控制预报成员在不同尺度上的扰动总能量分布,(b)14个集合成员小尺度(3 km)的扰动总能量,(c)14个集合成员中尺度(96 km)的扰动总能量,(d)14个集合成员大尺度(768 km)的扰动总能量 Fig. 4 Total perturbation energy distribution on different scales of the control member and 14 ensemble members at the initial time (a) total perturbation energy distribution on different scales of the control member, (b) total perturbation energy distribution on small scale (3 km) of 14 ensemble members, (c) total perturbation energy distribution at mesoscale (96 km) of 14 ensemble members, (d) total perturbation energy distribution on large scale (768 km) of 14 ensemble members |
因此,采用ADAS试验结合观测资料调整后的初始场增加了小尺度的信息,使得扰动总能量在不同尺度重新进行了分配,增加了小尺度的扰动总能量。
3.2 反射率因子诊断预报 3.2.1 反射率因子概率匹配集合平均的定性评估为了定性评估造成此次强对流天气的母体风暴预报效果,将两组集合预报试验反射率因子的概率匹配集合平均(PMEM)结果与观测进行了对比。上海南汇雷达12—14时的0.5°仰角反射率因子观测(图 5a~5c)显示,强对流系统向南偏东方向移动发展,强回波范围不断扩大,影响江苏南部、长江口区和上海北部,对流区位于回波移动方向前侧,对流区后侧有大片的层云区。CTRL试验的PMEM结果(图 5d~5f)显示,层状云区的覆盖范围比观测偏小,且与观测不同,CTRL试验预报的对流区位于层状云区中部,从回波移动速度来看也比观测偏慢,回波仅影响了江苏南部和长江口区的西部地区。ADAS试验的PMEM结果(图 5g~5i)与CTRL试验相比,预报的层状云区范围更广更接近观测,且ADAS试验预报出的对流区位于回波移动方向的前侧,移动速度也更接近于观测。但CTRL试验和ADAS试验预报的最强回波中心的强度与位置均与观测存在一定的偏差。
3.2.2 反射率因子的概率预报评估概率预报可以反映集合预报的不确定性,考虑到对流许可尺度集合预报对于时间和位置误差十分敏感,本文采用邻域集合概率(NEP; Roberts and Lean, 2008),该方法考虑了单个模式格点周围一定范围内的所有格点上所有集合成员的数据生成概率预报,而不仅仅依赖单个格点上的数据,因此NEP同时包含了空间和集合不确定性。
对流具有较小的空间尺度,并综合考虑模式3 km的格距,选取半径为6 km的圆形区域内所有格点来计算NEP。使用两组集合预报试验得到的上海南汇雷达12—14时的0.5°仰角反射率因子预报值分别计算了反射率因子>20 dBz(图 6)和>40 dBz(图 7)的NEP,并相应叠加了反射率因子观测值20和40 dBz等值线(红线)。
|
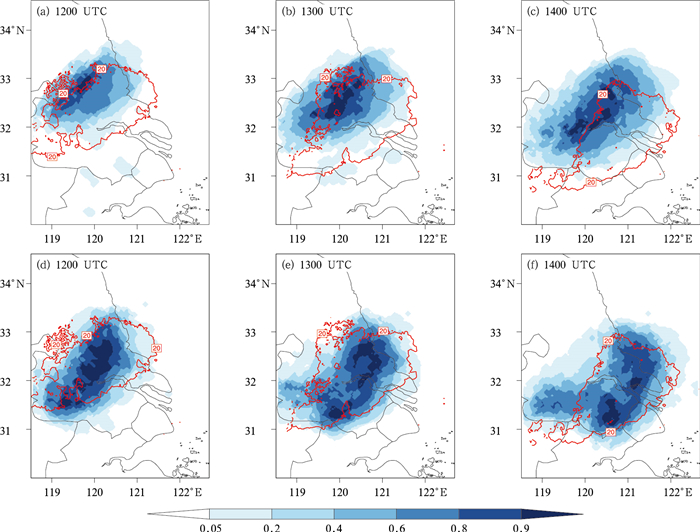
图 6 2015年4月28日12—14时上海南汇雷达0.5°仰角反射率因子>20 dBz的概率预报(填色)和观测反射率因子20 dBz的等值线(红线)
(a, b, c)CTRL试验的邻域集合概率(NEP),(d, e, f)ADAS试验的邻域集合概率(NEP)
Fig. 6 Neighborhood ensemble probability (shaded) of reflectivity (0.5° tilt) of Shanghai Nanhui Radar exceeding 20 dBz using a 6 km radius in 1200-1400 UTC 28 April 2015
(Thick red line represents observed reflectivity of 20 dBz)
(a, b, c) CTRL ensemble, (d, e, f) ADAS ensemble |
|
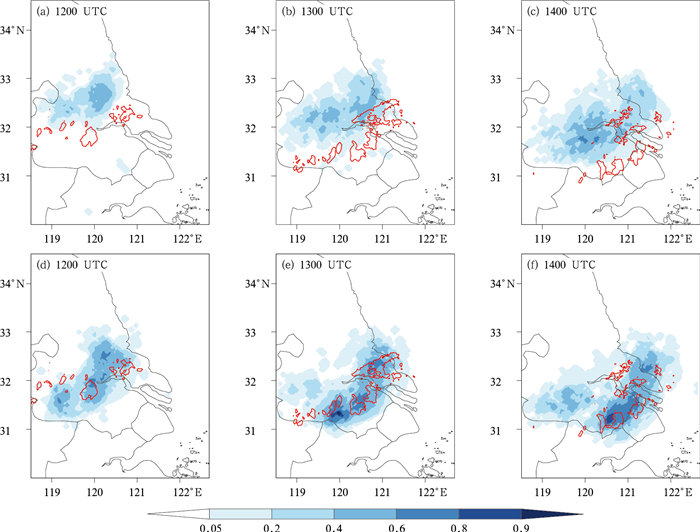
图 7 同图 6,但为反射率因子>40 dBz的概率预报(填色)和观测反射率因子40 dBz的等值线(红线) Fig. 7 Same as Fig. 6, but for the neighborhood ensemble probability (shaded) of reflectivity (0.5° tilt) of Shanghai Nanhui Radar exceeding 40 dBz (Thick red line represents observed reflectivity of 40 dBz) |
>20 dBz的范围反映了包含对流和层云区的总降水覆盖区域,ADAS试验的NEP预报与CTRL试验相比,在降水结构和位置预报都有显著改进(图 6)。ADAS试验(图 6d~6f)的较高概率(>0.6)覆盖区域的位置和形状均与观测20 dBz以上的区域近似吻合,而西南侧的移动速度比观测慢,14时预报的较高概率区域比观测偏北。CTRL试验(图 6a~6c)显示较高概率(>0.6)范围仅覆盖观测20 dBz以上区域的一半,而14时预报的高概率(>0.8)区域更是有一部分落在了观测20 dBz以上的范围以外。
>40 dBz的区域用来反映对流降水区域,相比总降水覆盖区域,对流降水区域范围较小且较为分散,因此,对于对流降水区域的概率预报呈现较大的误差。在CTRL试验中(图 7a~7c)仅较低概率(0.05~0.4)与观测40 dBz以上区域有较小的重合,较大概率的区域均落在观测40 dBz以上的区域以外。而ADAS试验(图 7d~7f)相比CTRL试验与观测40 dBz以上的区域有更大的重合,概率也较大(0.4~0.8),但ADAS试验中等概率(0.4~0.8)的覆盖范围较观测40 dBz以上的区域偏大。
3.2.3 反射率因子的定量评估为了定量比较反射率因子预报结果,基于图 5中上海南汇雷达0.5°仰角反射率因子的PMEM预报,分别计算了两组集合预报不同阈值下的ETS和偏差(Bias)评分(图 8)。
|
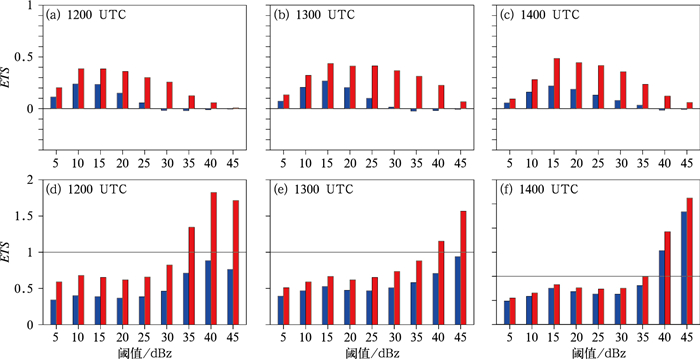
图 8 2015年4月28日12—14时上海南汇雷达0.5°仰角不同阈值的反射率因子在CTRL试验(蓝色)和ADAS试验(红色)的概率匹配集合平均(PMEM)结果中的(a, b, c)ETS评分,(d, e, f)Bias评分 Fig. 8 ETS (a, b, c), Bias (d, e, f) of different reflectivity (0.5° tilt) threshold using probability matching ensemble mean of CTRL (blue) and ADAS (red) ensemble in 1200-1400 UTC 28 April 2015 |
从ETS评分来看(图 8a~8c),ADAS试验相比CTRL试验有了显著的改善,对于20 dBz的阈值(反映了包含对流和层云区的总降水),CTRL试验在12—14时三个整点时次的ETS在0.1~0.2,而ADAS试验则提高到了0.4~0.5,对于40 dBz的阈值(反映了对流降水区域),CTRL试验的ETS评分均为负值,而ADAS试验则将其提高到了0.1 ~0.2。
Bias评分为预报满足标准的格点数与观测满足标准的格点数之比,当预报无偏差时,Bias=1,若Bias>1时,该反射率因子阈值以上的预报范围偏大,反之预报范围偏小。图 8d~8f中Bias评分显示,ADAS试验相比CTRL试验在所有反射率因子阈值上的预报范围都有所扩大,但是,两组集合在30 dBz阈值以下的预报范围依然比观测偏小。
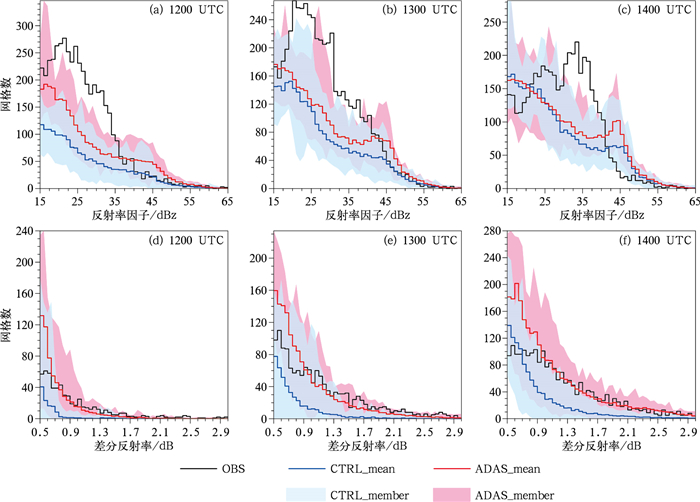
为了避免由于观测与预报之间存在空间偏差而导致较低的评分,图 9绘制了CTRL试验和ADAS试验在不同变量阈值下格点数统计直方图,为了能与观测进行对比,对CTRL试验和ADAS试验所有成员的预报统计值均除以集合大小,进行归一化得到平均值CTRL_mean和ADAS_mean,而图 9中的阴影则为对应阈值下成员预报统计得到的最大和最小值所围成的区域CTRL_member和ADAS_member。由于观测的层云区域面积大于模式预报,因此观测的反射率因子直方图存在明显的峰值(图 9a~9c),且随着预报时效的增加,观测的峰值逐渐往更高的反射率因子值移动,12时和13时的观测峰值位于20~25 dBz,而14时的观测峰值移到了30~35 dBz,CTRL_mean和ADAS_mean不存在明显的峰值,从15 dBz起随着反射率因子值的增加格点数逐渐减少,仅14时的ADAS_mean在45 dBz附近存在一个次峰值。由于模式预报的强对流区范围比观测大,因此与观测相比,预报>40 dBz的格点数偏多,特别是ADAS_mean在40~50 dBz范围内偏多显著。从CTRL_member和ADAS_member来看,有部分成员的峰值达到与观测相当,但强度略有偏差,在观测峰值的范围内,ADAS_member中的最大值比CTRL_member中的最大值更为接近观测。
|
图 9 2015年4月28日12—14时上海南汇雷达0.5°仰角观测(黑线)、CTRL试验平均(蓝线)、ADAS试验平均(红线)、CTRL试验成员(蓝色阴影)和ADAS试验成员(红色阴影)格点数直方图 (a, b, c)反射率因子,(d, e, f)差分反射率 Fig. 9 Grid number histogram of observation (black line), CTRL ensemble mean (blue line), ADAS ensemble mean (red line), CTRL ensemble member (blue shaded) and ADAS ensemble member (red shaded) at 0.5° tilt of Shanghai Nanhui Radar at 1200-1400 UTC 28 April 2015 (a, b, c) reflectivity, (d, e, f) differential reflectivity |
图 10与图 5相似,但计算的是差分反射率。图 10a~10c的观测显示,12时的差分反射率值和分布范围均较小,对应图 5a中反射率因子观测有两个大值中心,一个位于江苏省的无锡和常州市附近,另一个位于江苏省南通市附近。差分反射率的大值区仅位于南通市附近,因此位于无锡和常州市附近的对流单体对应高反射率因子和低差分反射率,满足出现冰雹的判断标准,而另一个位于南通市附近的对流单体则对应高反射率因子和高差分反射率,满足出现强降水(大粒子)的判断标准。13时和14时的差分反射率值逐渐增大,分布范围逐步扩大,与此对应,强回波的范围也不断扩大(图 5b, 5c),表明出现强降水(大粒子)的范围和强度都有所增大,而回波西南侧的高反射率因子依然对应较低的差分反射率值,满足出现冰雹的判断标准。
从两组集合预报试验PMEM的结果看,CTRL试验预报的差分反射率范围和值的大小均比观测偏小(图 10d~10f),且由于CTRL试验预报的回波移动速度比观测偏慢,因此差分反射率的大值区位置比观测偏北,虽然ADAS试验预报14时的差分反射率与观测相比强度偏强,但整体的预报位置和强度与实况更为接近。
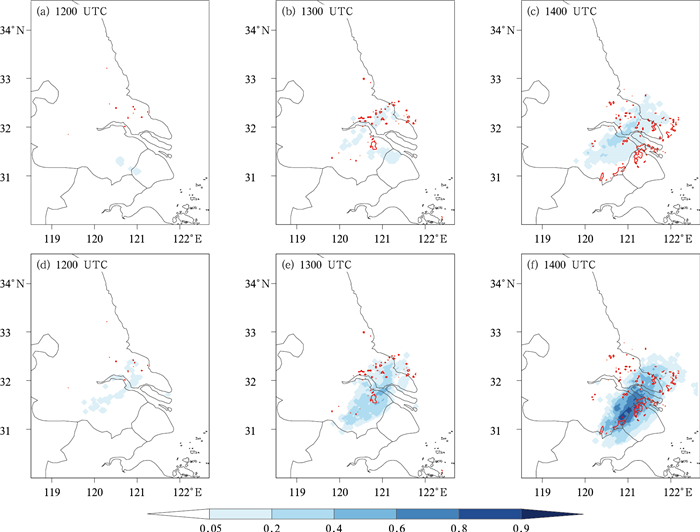
3.3.2 差分反射率的概率预报评估在3.2.2节中,基于20和40 dBz的阈值对总降水和对流降水分别进行了概率预报评估,而差分反射率的大值可以用来区分强降水中的大粒子,选用2.0 dB阈值来计算两组集合预报试验得到的差分反射率NEP(图 11),相应叠加了观测值2.0 dB等值线(红线)。
|
图 11 同图 6,但为差分反射率>2.0 dB的概率预报(填色)和观测差分反射率2.0 dB的等值线(红线) Fig. 11 Same as Fig. 6, but for neighborhood ensemble probability (shaded) of differential reflectivity (0.5° tilt) (Thick red line represents observed differential reflectivity of 2.0 dB) |
CTRL试验预报2.0 dB以上差分反射率的概率较低(< 0.4),且位置与观测存在明显的差异,ADAS试验预报在12时低概率(0.05~0.2)区域与观测的2.0 dB等值线有一定重合,而在13时和14时中等概率(0.2~0.6)区域虽然覆盖范围较大,但几乎涵盖了观测的2.0 dB等值线范围,且整个区域呈东北—西南向块状,与观测分布型类似。
3.3.3 差分反射率的定量评估图 9d~9f中对差分反射率也绘制了两组试验的格点数直方图。CTRL_mean和ADAS_mean在差分反射率预报的直方图分布形态与观测较为接近,无明显峰值,从0.5 dB起随着差分反射率值的增加格点数逐渐减少,当冰雹与降水混合时,差分反射率值较小且呈正值,而差分反射率的大值(>2.0 dB)则由强降水中的大粒子所导致。在较小的差分反射率值范围内(0.5~1.5 dB),ADAS_mean的预报范围大于观测,而CTRL_mean的预报范围则小于观测,且CTRL_member和ADAS_member中的最大值都超过了观测,而在差分反射率的大值区(>2.0 dB)内,ADAS_mean与观测较为一致,CTRL_mean的预报范围则小于观测,且CTRL_member中的最大值依然小于观测,即CTRL试验中所有的成员对差分反射率的大值区预报范围都偏小。
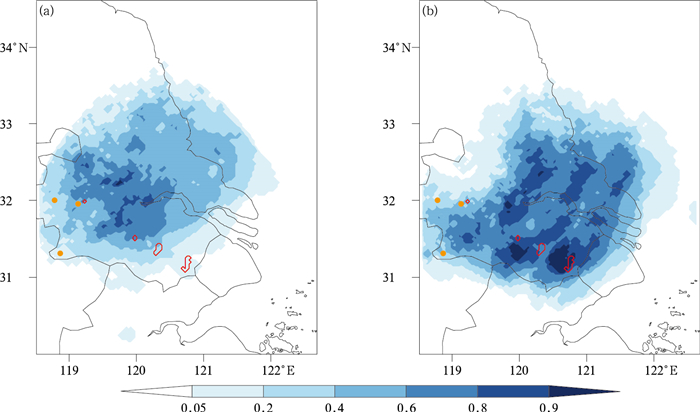
3.4 冰雹最大直径诊断预报上文根据反射率因子阈值区分了总降水和对流降水区域,根据差分反射率阈值区分了大粒子降水,而在此次强对流过程中还伴随有冰雹。冰雹是一种固态降水物,直径一般为5~50 mm,大的有时可达100 mm以上,28日12—14时具备人工观测的国家级站点中观测到直径>5 mm冰雹的站点(图 12中黄点)包括江苏南京站(9 mm)、高淳站(23 mm)和句容站(10 mm)。对两组集合预报分别计算了各个成员冰雹最大直径的预报值(maximum predicted hail diameter, MPHD, 计算方法详见附录),并选取5 mm作为阈值,在半径6 km的圆形区域内来计算NEP。图 12中阴影部分为两组集合预报试验12—14时3个整点时刻每个格点对应的最大NEP。由于具备人工观测的国家级站点分布相对稀疏,因此,使用上海南汇雷达12—14时的0.5°仰角观测的反射率因子(图 5a~5c)>55 dBz、差分反射率(图 10a~10c) < 1.5 dB且相关系数(图略) < 0.95的区域来辅助判断冰雹落区(红色等值线)。
|
图 12 2015年4月28日上海南汇雷达0.5°仰角冰雹最大直径预报(MPHD)>5 mm的概率预报(填色)、台站记录的冰雹观测(黄点)和双偏振雷达观测到的冰雹区域(红色等值线) 12—14时3个时次CTRL试验(a)和ADAS试验(b)的邻域集合概率(NEP)最大值 Fig. 12 Neighborhood ensemble probability (shaded) of maximum predicted hail diameter exceeding 5 mm using a 6 km radius in 1200-1400 UTC 28 April 2015
(Yellow dots are ground hail observation records and red thick lines are the hail area observed by dual-polarization radar)
(a) maximum value of CTRL ensemble, (b) maximum value of ADAS ensemble |
通过雷达判定的降雹区主要集中在江苏省南部的常州、无锡和苏州地区,均位于对流区域的西南侧,与3.3.1节中对观测差分反射率的分析结果一致。两组集合预报试验5 mm阈值的NEP分布范围较广,CTRL试验的概率值较小,多集中在0.4~0.6,而ADAS试验的概率值达到了0.8以上,虽然两组集合预报试验在整个对流区域均预报出现冰雹的概率,但西南侧的概率值较大,与观测相符合。观测到冰雹的3个站点均落在两组集合试验预报的NEP范围内,概率值大小相当。而对于雷达判定的冰雹落区,由于CTRL试验中回波移动速度较慢,未预报出苏州的降雹概率,常州和无锡则位于中低概率区(0.2~0.6),且CTRL试验的高概率区无观测对应;而ADAS试验中预报常州、无锡和苏州地区出现5 mm以上冰雹的概率值高达0.6~0.9,均落在ADAS试验预报的高概率(>0.8)降雹区附近。
4 结论和讨论针对2015年4月28日发生在华东地区的一次伴随短时强降水和冰雹的强对流天气过程,使用GEFS作为模式的初始场和侧边界场,构造了两组水平分辨率3 km的集合预报对比试验,其中,CTRL试验的初始场直接采用WRF前处理系统WPS得到,ADAS试验的初始场采用ADAS资料分析系统得到,结合了观测资料,更接近真实的大气状态。通过对初始时刻水物质的分布和初始扰动总能量在不同尺度上分解分析显示,与CTRL试验相比较,ADAS试验经过云分析调整了初始时刻的水物质分布,同时采用逐步订正法对常规资料进行了客观分析,增加了初始场的小尺度信息。两组集合预报试验的对比时段选择在回波进入上海南汇双偏振雷达观测范围内,且该时段内发生了短时强降水和冰雹。针对强对流在较小的范围内变化快及对时空误差敏感的特征,文中集合平均采用概率匹配集合平均,概率预报采用6 km领域集合概率预报,对两组集合预报试验进行了定性和定量的评估,主要结论如下:
(1) 对反射率因子集合平均预报的评估显示,ADAS试验的对流区与观测一致,位于回波移动方向的前侧,移动速度更接近于实况,而CTRL试验的对流区则位于层状云区中部,回波移动速度也比实况偏慢,这些都导致了两组集合预报试验对双偏振变量和冰雹的预报产生较大的差异。对总降水区和对流降水区的集合概率预报进行评估显示,相比总降水覆盖区域,对流降水区域范围较小且较为分散,因此,两组集合预报试验对于对流降水区域的概率预报均呈现较大的误差,但ADAS试验对降水结构和位置预报都比CTRL试验有显著改进,且ADAS试验在基于反射率因子不同阈值ETS评分和格点数直方图(不考虑空间偏差)计算的基础上与CTRL试验相比具有更高的预报技巧。
(2) 由于双偏振变量特征通常可以反映出小尺度的对流系统物理过程,而ADAS试验调整了初始水物质分布并在初始场中增加了更多的小尺度信息,对差分反射率的评估显示,ADAS试验预报的差分反射率预报虽然强度偏强,但整体的位置和强度与实况更为接近。差分反射率的大值可以用来区分强降水中的大粒子,对两组试验>2.0 dB的集合概率预报进行评估显示,ADAS试验概率预报几乎涵盖了观测的2.0 dB等值线范围,且与观测分布型相似,通过格点数直方图的定量评估也显示出,ADAS试验在大粒子预报方面具有更高的技巧,对于此次过程强降水的微物理相关特征具有更好的描述。
(3) 冰雹概率预报结果表明,预报时效可达12~14 h,ADAS试验的概率值大于CTRL试验,且通过雷达观测判定的冰雹落区均位于ADAS试验预报的高概率降雹区附近,对冰雹落区的预报具有较好的指示意义。
在本个例中,ADAS试验初始分析场融合了多种观测资料,调整了模式初始水物质分布,并在初始场中增加了更多的小尺度信息,更接近真实的大气状态,使对流许可尺度集合预报具有更高的可信度。
本文仅针对一个强对流个例进行了初步讨论,关于初始多源融合分析场对于对流许可尺度集合预报影响的研究还有待于在下阶段进行更广泛的数值预报试验分析。此外,后续研究可以开展针对更多其他双偏振变量的预报与观测实况的对比检验,例如相关系数、差分传播相位和差分相位系数等,从而进一步评估模式对微物理过程描述的准确性。
附录 冰雹最大直径的计算方法许多研究表明γ分布是云滴和降水粒子较为合理的近似分布形式,因此在MY2微物理方案中假设冰雹粒子的数浓度分布(particle size distribution, PSD)满足γ分布函数(Ulbrich, 1983)
| $N(D)=N_{0} D^{a} \mathrm{e}^{-\lambda D} $ | (1) |
式中,N(D)是给定直径D的粒子数,N0称为截断参数,α是形状参数,λ为斜率参数。由于MY2方案中的预报变量为粒子混合比和数浓度,因此,通常将α的取值固定为0,转化为两个未知量N0和λ的反演。根据Milbrandt and Yau (2005)文中可知
| $ N_{0}=N_{\mathrm{T}} \frac{1}{\mathit{\Gamma}(1+\alpha)} \lambda^{1+\alpha} $ | (2) |
式中,NT为总的数浓度,当α的取值固定为0时,式(2)简化为
| $ N_{0}=N_{T} \frac{1}{\mathit{\Gamma}(1)} \lambda $ | (3) |
将式(3)代入式(1),且当α的取值固定为0时,可得
| $ N(D)=N_{T} \frac{1}{\mathit{\Gamma}(1)} \lambda \mathrm{e}^{-\lambda D} $ | (4) |
将大于某个指定粒子直径大小D*的总粒子浓度Nh*{D*}定义为
| $ N_{h}^{*}\left\{D^{*}\right\}=\int_{D^{*}}^{\infty} N(D) \mathrm{d} D $ | (5) |
将式(4)代入式(5)积分得到
| $ N_{h}^{*}\left\{D^{*}\right\}=\int_{D^{*}}^{\infty} N_{T} \frac{1}{\mathit{\Gamma}(1)} \lambda \mathrm{e}^{-\lambda D} \mathrm{d} D=N_{T} \frac{1}{\mathit{\Gamma}(1)} \mathrm{e}^{-\lambda D} $ | (6) |
通常给定阈值NCRIT*=10-4 m-3(Milbrandt and Yau, 2006),满足条件Nh*{D*}>NCRIT*的最小直径DCRIT*定义为数值模式预测的冰雹最大直径。
陈涛, 林建, 张芳华, 等, 2017. "16·7"华北极端强降水过程对流尺度集合模拟试验不确定性分析[J]. 气象, 43(5): 513-527. Chen T, Lin J, Zhang F H, et al, 2017. Uncertainty analysis on the July 2016 extreme precipitation event in North China using convection allowing ensemble simulation[J]. Meteor Mon, 43(5): 513-527 (in Chinese).
|
李佳, 陈葆德, 黄伟, 等, 2017. 对流尺度数值预报中的云物理初始化方法改进及个例试验[J]. 气象学报, 75(5): 771-783. Li J, Chen B D, Huang W, et al, 2017. Cloud physics initialization for convection-scale NWP:scheme improvements and a case study[J]. Acta Meteor Sin, 75(5): 771-783 (in Chinese).
|
李俊, 杜钧, 刘羽, 等, 2017. 不同扰动方法集合离散度演变的异同性暨地形扰动初探[J]. 气象学报, 75(1): 123-146. Li J, Du J, Liu Y, et al, 2017. Similarities and differences in the evolution of ensemble spread using various ensemble perturbation methods including topography perturbation[J]. Acta Meteor Sin, 75(1): 123-146 (in Chinese).
|
穆瑞琪, 孙建印, 吕翔, 等, 2015.2015年4月27日至28日徐州强对流天气过程浅析[C]//第32届中国气象学会年会s1灾害天气监测、分析与预报.天津: 中国气象学会. Mu R Q, Sun J Y, Lü X, et al, 2015.Analysis of the convective weather process happened in Xuzhou during April 27 to 28, 2015[C]//Annual Meeting of the Chinese Meteorological Society s1 Disaster Weather Monitoring, Analysis and Forecast.Tianjin: Chinese Meteorological Society(in Chinese).
|
谭燕, 陈德辉, 2008. 河南"75.8"大暴雨的中尺度集合预报试验[J]. 气象, 34(9): 10-21. Tan Y, Chen D H, 2008. Mesoscale ensemble forecasts on "75.8" heavy rain in Henan[J]. Meteor Mon, 34(9): 10-21 (in Chinese).
|
吴海英, 陈海山, 刘梅, 等, 2017. 长生命史超级单体结构特征与形成维持机制[J]. 气象, 43(2): 141-150. Wu H Y, Chen H S, Liu M, et al, 2017. Structure characteristics, formation and maintenance mechanism of supercell with long life cycle[J]. Meteor Mon, 43(2): 141-150 (in Chinese).
|
尹春光, 王勤典, 陈浩君, 等, 2015.上海WSR-88D雷达双偏振升级实施概要[C]//第32届中国气象学会年会s16地基遥感观测技术与应用.天津: 中国气象学会. Yin C G, Wang Q D, Chen H J, et al, 2015.Shanghai WSR-88D radar dual polarization upgrade implementation summary[C].Annual Meeting of the Chinese Meteorological Society s16 Ground-based Remote Sensing Observation Technology and Application.Tianjin: Chinese Meteorological Society(in Chinese).
|
庄潇然, 闵锦忠, 蔡沅辰, 等, 2016. 不同大尺度强迫条件下考虑初始场与侧边界条件不确定性的对流尺度集合预报试验[J]. 气象学报, 74(2): 244-258. Zhuang X R, Min J Z, Cai Y C, et al, 2016. Convective-scale ensemble prediction experiments under diffe-rent large-scale forcing with consideration of uncertainties in initial and lateral boundary condition[J]. Acta Meteor Sin, 74(2): 244-258 (in Chinese).
|
Bringi B N, Chandrasekar V, 2001. Polarimetric Doppler Weather Radar[M].
Cambridge: Cambridge University Press: 636.
|
Clark A J, Weiss S J, Kain J S, et al, 2012. An overview of the 2010 hazardous weather testbed experimental forecast program spring experiment[J]. Bull Amer Meteor Soc, 93(1): 55-74. DOI:10.1175/BAMS-D-11-00040.1
|
Dawson Ⅱ D T, Mansell E R, Jung Y S, et al, 2014. Low-level ZDR signatures in supercell forward flanks:the role of size sorting and melting of hail[J]. J Atmos Sci, 71(1): 276-299. DOI:10.1175/JAS-D-13-0118.1
|
Ebert E E, 2001. Ability of a poor man's ensemble to predict the probability and distribution of precipitation[J]. Mon Wea Rev, 129(10): 2461-2480. DOI:10.1175/1520-0493(2001)129<2461:AOAPMS>2.0.CO;2
|
Fang X Q, Kuo Y H, Wang A Y, 2011. The impacts of Taiwan topography on the predictability of typhoon Morakot's record-breaking rainfall:a high-resolution ensemble simulation[J]. Wea Forecasting, 26(5): 613-633. DOI:10.1175/WAF-D-10-05020.1
|
Hu M, Xue M, Brewster K, 2006. 3DVAR and cloud analysis with WSR-88D level-Ⅱ data for the prediction of the Fort Worth, Texas, tornadic thunderstorms.Part Ⅰ:Cloud analysis and its impact[J]. Mon Wea Rev, 134(2): 675-698. DOI:10.1175/MWR3092.1
|
Johnson A, Wang X G, Xue M, et al, 2014. Multiscale characteristics and evolution of perturbations for warm season convection-al-lowing precipitation forecasts:dependence on background flow and method of perturbation[J]. Mon Wea Rev, 142(3): 1053-1073. DOI:10.1175/MWR-D-13-00204.1
|
Jung Y, Xue M, Tong M J, 2012. Ensemble kalman filter analyses of the 29-30 May 2004 oklahoma tornadic thunderstorm using one- and two-moment bulk microphysics schemes, with verification against polarimetric radar data[J]. Mon Wea Rev, 140(5): 1457-1475. DOI:10.1175/MWR-D-11-00032.1
|
Jung Y, Xue M, Zhang G F, 2010. Simulations of polarimetric radar signatures of a supercell storm using a two-moment bulk microphysics scheme[J]. J Appl Meteor Climatol, 49(1): 146-163. DOI:10.1175/2009JAMC2178.1
|
Jung Y, Zhang G F, Xue M, 2008. Assimilation of simulated polarimetric radar data for a convective storm using the ensemble Kalman filter.Part Ⅰ:observation operators for reflectivity and polarimetric variables[J]. Mon Wea Rev, 136(6): 2228-2245. DOI:10.1175/2007MWR2083.1
|
Kumjian M R, Ryzhkov A V, 2008. Polarimetric signatures in supercell thunderstorms[J]. J Appl Meteor Climatol, 47(7): 1940-1961. DOI:10.1175/2007JAMC1874.1
|
Li X L, Mecikalski J R, 2012. Impact of the dual-polarization Doppler radar data on two convective storms with a warm-rain radar forward operator[J]. Mon Wea Rev, 140(7): 2147-2167. DOI:10.1175/MWR-D-11-00090.1
|
Milbrandt J A, Yau M K, 2005. A multimoment bulk microphysics parameterization.Part Ⅰ:analysis of the role of the spectral shape parameter[J]. J Atmos Sci, 62(9): 3051-3064. DOI:10.1175/JAS3534.1
|
Milbrandt J A, Yau M K, 2006. A multimoment bulk microphysics parameterization.Part Ⅲ:control simulation of a hailstorm[J]. J Atmos Sci, 63(12): 3114-3136. DOI:10.1175/JAS3816.1
|
Posselt D J, Li X L, Tushaus S A, et al, 2015. Assimilation of dual-polarization radar observations in mixed- and ice-phase regions of convective storms:information content and forward model errors[J]. Mon Wea Rev, 143(7): 2611-2636. DOI:10.1175/MWR-D-14-00347.1
|
Putnam B J, Xue M, Jung Y, et al, 2014. The analysis and prediction of microphysical states and polarimetric radar variables in a mesoscale convective system using double-moment microphysics, multinetwork radar data, and the ensemble Kalman filter[J]. Mon Wea Rev, 142(1): 141-162. DOI:10.1175/MWR-D-13-00042.1
|
Putnam B J, Xue M, Jung Y, et al, 2017a. Simulation of polarimetric radar variables from 2013 CAPS spring experiment storm-scale ensemble forecasts and evaluation of microphysics schemes[J]. Mon Wea Rev, 145(1): 49-73. DOI:10.1175/MWR-D-15-0415.1
|
Putnam B J, Xue M, Jung Y, et al, 2017b. Ensemble probabilistic prediction of a mesoscale convective system and associated polarimetric radar variables using single-moment and double-moment microphysics schemes and EnKF radar data assimilation[J]. Mon Wea Rev, 145(6): 2257-2279. DOI:10.1175/MWR-D-16-0162.1
|
Roberts N M, Lean H W, 2008. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events[J]. Mon Wea Rev, 136(1): 78-97. DOI:10.1175/2007MWR2123.1
|
Roebber P J, Schultz D M, Colle B A, et al, 2004. Toward improved prediction:High-resolution and ensemble modeling systems in operations[J]. Wea Forecasting, 19(5): 936-949. DOI:10.1175/1520-0434(2004)019<0936:TIPHAE>2.0.CO;2
|
Snook N, Jung Y, Brotzge J, et al, 2016. Prediction and ensemble forecast verification of hail in the supercell storms of 20 May 2013[J]. Wea Forecasting, 31(3): 811-825. DOI:10.1175/WAF-D-15-0152.1
|
Ulbrich C W, 1983. Natural variations in the analytical form of the raindrop size distribution[J]. J Climate Appl Meteor, 22(10): 1764-1775. DOI:10.1175/1520-0450(1983)022<1764:NVITAF>2.0.CO;2
|
Vié B, Nuissier O, Ducrocq V, 2011. Cloud-resolving ensemble simulations of mediterranean heavy precipitating events:uncertainty on initial conditions and lateral boundary conditions[J]. Mon Wea Rev, 139(2): 403-423. DOI:10.1175/2010MWR3487.1
|
Vivekanandan J, Adams W M, Bringi V N, 1991. Rigorous approach to polarimetric radar modeling of hydrometeor orientation distributions[J]. J Appl Meteor, 30(8): 1053-1063. DOI:10.1175/1520-0450(1991)030<1053:RATPRM>2.0.CO;2
|
Xue M, Wang D H, Gao J D, et al, 2003. The advanced regional prediction system (ARPS), storm-scale numerical weather prediction and data assimilation[J]. Meteor Atmos Phys, 82(1): 139-170.
|
Zhang G F, Vivekanandan J, Brandes E, 2001. A method for estimating rain rate and drop size distribution from polarimetric radar measurements[J]. IEEE Trans Geosci Remote Sens, 39(4): 830-841. DOI:10.1109/36.917906
|
 2019, Vol. 45
2019, Vol. 45 
